En pendel är en mekanisk anordning med periodisk rörelse. Pendelns mekaniska energi bevaras och omvandlas kontinuerligt mellan potentiell energi och rörelseenergi, se oscillation.

Den vanligaste varianten är gravitationspendeln. Dess period beror av endast två faktorer – tyngdaccelerationen och avståndet mellan fästpunkten och pendelns masscentrum. Denna pendel uppfanns av Galileo Galilei på 1500-talet^{[källa behövs]} och har framför allt använts i urverk. En annan variant är torsionspendeln, där en deformerbar kropp vrids fram och tillbaka av sin egen energi.

I vissa delar av världen, framför allt i södra Europa, har pendeln tillskrivits övernaturliga egenskaper och den har använts på samma sätt som en slagruta för att finna vattenkällor.

Pendeln har genom tiderna använts både praktiskt och experimentellt. Den används i klockor och den användes tidigt för att undersöka kroppars fallrörelse. En pendel som består av en punktformad massa som är upphängd i en oelastisk tråd brukar betecknas som en matematisk pendel. Ur denna kan svängningstiden T, för små vinklar, härledas till att endast bero på trådens längd l och tyngdaccelerationen g:

Eftersom trådens längd och svängningstiden går att mäta får man ett bra verktyg för att experimentellt mäta också tyngdaccelerationen.

Om svängningsvinkeln inte är liten, kan man inte göra antagandet att , varvid beräkningarna blir betydligt mer komplicerade. Då blir istället svängningstiden en funktion av den mer komplicerade elliptiska integralen av första slaget, där är pendelns största utslag.

.

Om man istället använder det mer lättberäknade aritmetisk-geometriskt medelvärdet blir uttrycket:

Vi ser här att när är nära 0, blir cosinus nära 1 och medelvärdet blir också nära 1 och blir därför närmast detsamma som det förenklade uttrycket ovan. Om pendeln är nära att ställa sig helt rakt upp, kommer pendlingstiden att gå emot oändligheten.^[1]

För en verklig, fysikalisk pendel, där tyngden är fördelad mellan kulan och upphängningsanordningen, gäller formeln

där I är pendelns tröghetsmoment med avseende på axeln, M är massan och h avståndet från axeln till pendelns tyngdpunkt. Om man sätter I/Mh = l’ får man samma ekvation som för den matematiska pendeln varvid l’ kallas den reducerade pendellängden. Pendelns konstanta svängningstid utnyttjas i pendeluret som infördes av Christian Huygens 1656.^[2]

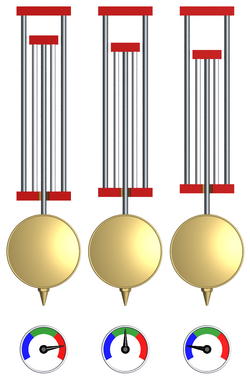
En kompensationspendel är en pendel, som är så sammansatt, att de av temperaturväxlingar åstadkomna förändringarna av pendellängden utjämnas och svängningstiden således hålls konstant. Den mest använda pendeln av detta slag är den av John Harrison 1725 konstruerade så kallade rostpendeln, som är sammansatt av metaller med olika utvidgningsförmåga för värme. Kompensationen vinnes därigenom, att de kortare zinkstängerna, som förlänger sig mer än stålstängerna, vid ökad temperatur lyfter pendelkulan lika högt, som den sänkes till följd av de sistnämnda stängernas samtida förlängning.

Den så kallade kvicksilverpendeln, konstruerad av George Graham (1721), består av en pendelstång (av metall), på vilken fästs en glascylinder med kvicksilver. Vid temperaturförändringar växlar tyngdpunktens läge i kvicksilvret, och därigenom kan, om kvicksilverkolonnens längd avpassas rätt, pendellängden bibehålls oförändrad.

Fjäderkompensation åstadkoms därigenom, att man vinkelrätt mot pendelstången i svängningsplanet fäster en fjäder eller skiva, bestående av två hoplödda metaller med olika termisk utvidgningsförmåga, den med mindre utvidgning på övre, den med större på undre sidan. Är fjädern rak vid en viss temperatur, kommer den att vid högre värmegrad böja sig uppåt och vid lägre nedåt med sina ändar. Om pendelstången genom värme förlängs och dess tyngdpunkt därför sänks, kommer fjäderns tyngdpunkt att förflyttas i motsatt led; verkan därav blir betydligt kraftigare, om på fjäderns ändar sätts små kulor. Själva fjädern eller lamellen görs vanligen av järn och koppar med järnet på övre sidan.

När den på 1890-talet upptäckta legeringen invar (järn med 36,2 procent nickel), vars termiska utvidgning är praktiskt taget obefintlig, började användas till pendelstänger blev kompensationspendeln överflödig.

• Pendel i Nordisk familjebok (andra upplagan, 1915)

• Invar
• Pendelur
• Pierre Jaquet-Droz
• Foucaultpendel
• Pendeltåg