Twierdzenie Talesa


Twierdzenie Talesa – twierdzenie geometrii euklidesowej, konkretniej planimetrii, obowiązujące też w geometrii afinicznej. Dotyczy ono stosunków długości odcinków utworzonych przez cztery proste, z których dwie są do siebie równoległe, a pozostałe dwie – nie.
Tradycja przypisuje jego sformułowanie Talesowi z Miletu[1][2][3].
Twierdzenie
Jeżeli ramiona kąta przetniemy dwiema prostymi równoległymi nieprzechodzącymi przez wierzchołek kąta, to odpowiednie odcinki wyznaczone przez te proste na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu kąta[2][3].
Przy oznaczeniach na rysunku obok.
Jeśli
to zachodzi każda z trzech równości:
Trzy równości można połączyć w jedną potrójną równość:
- Uwaga 1.
Twierdzenie zachodzi również, jeśli proste równoległe przecinają ramiona kątów wzajemnie wierzchołkowych.
- Uwaga 2.
Twierdzenie może być sformułowane bez użycia pojęcia kąta:
- Jeśli wiązka prostych parami równoległych przecina dwie nierównoległe do siebie proste to odpowiednie odcinki wyznaczone przez tę wiązkę na prostej są proporcjonalne do odpowiednich odcinków wyznaczonych przez tę wiązkę na prostej
lub jeszcze ogólniej
- Rzutowanie równoległe zachowuje proporcje długości na prostych, tzn. stosunek długości odcinków współliniowych jest niezmiennikiem rzutowania równoległego.

Twierdzenie odwrotne
Zachodzi również następujące twierdzenie odwrotne[1].
Jeśli ramiona kąta o wierzchołku przecięte są dwiema prostymi przy czym punkty należą do jednego ramienia kąta, punkty do drugiego oraz:
to tzn. proste są równoległe[3].
- Uwaga
Gdyby warunek w założeniu zastąpić np. następującym:
to założenia należałoby uzupełnić o informacje o uporządkowaniu punktów, np.
- punkt leży między punktami punkt leży między punktami
Dowód na gruncie geometrii syntetycznej
(szkic) twierdzenie Talesa można dowieść korzystając z przejścia granicznego i dobrze określonej miary (np. Lebesgue’a na płaszczyźnie): stosunkowo łatwy jest dowód, gdy podobnie gdy podzieli się odcinki w stosunku wymiernym, przypadek niewymierny dowodzi się przez przybliżenia za pomocą przejścia granicznego.
Dowód na gruncie geometrii afinicznej
Niech wektory będą liniowo niezależne i niech dla pewnych tzn.
Jeśli czyli dla pewnego to
Przyrównując skrajne wyrażenia, redukując i porządkując:
Ponieważ są liniowo niezależne, więc czyli Stąd
Odwrotnie, jeśli czyli to
Stąd
Dowód Euklidesa

Najstarszy zachowany dowód twierdzenia Talesa zamieszczony jest w VI. księdze Elementów Euklidesa.
Dowód oparty jest na dwóch lematach:
- Jeśli dwa trójkąty mają równe wysokości, to stosunek ich pól jest równy stosunkowi długości ich podstaw.
- Jeśli dwa trójkąty mają wspólną podstawę i równe wysokości, to ich pola są równe.
- Dowód
Niech oznacza pole powierzchni trójkąta
Trójkąty i mają wspólną wysokość więc na mocy lematu 1.:
Dodatkowo trójkąty i mają wspólną podstawę i równe wysokości dlatego na mocy lematu 2:
- stąd
Trójkąty i mają wspólną wysokość, więc zgodnie z lematem 1:
Przyrównując do siebie te równości otrzymuje się
- Uwaga
W powyższym rozumowaniu korzysta się z faktu, iż pole trójkąta liczone dla jednego boku jako podstawy i opuszczonej na niego wysokości jest równe polu liczonemu dla innego boku jako podstawy i opuszczonej na ten bok wysokości. Jest to dość silna własność funkcji pola (wyżej korzysta się z niej w drugim zdaniu dowodu), jednak nie jest ona niezbędna do dowiedzenia twierdzenia Talesa i w szkolnej matematyce cicho się ją zakłada. Notabene własność tę można udowodnić właśnie z twierdzenia Talesa. To prowadzi do błędnego koła.
Wniosek
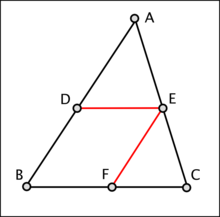
Przy oznaczeniach na rysunku obok.
Jeśli
to zachodzi każda z dwóch równości:
Dwie równości można połączyć w jedną potrójną równość:
Zastosowania
Podział odcinka w danym stosunku
Poniższa konstrukcja była podstawą greckiej arytmetyki – pozwalała mnożyć i dzielić odcinki, utożsamiane przez Greków z liczbami.
- Zadanie
- Dane są dwa odcinki o długościach i Dany odcinek podziel w stosunku
- Rozwiązanie
- Z punktu należy poprowadzić dwie niewspółliniowe półproste. Na jednej z nich odkładamy kolejno długości i a na drugiej odcinek Prowadzimy prostą przez punkt leżący w odległości na pierwszej półprostej oraz punkt leżący na drugiej, a następnie prostą do niej równoległą przechodzącą przez punkt leżący na drugiej półprostej w odległości od punktu która wyznacza na prostej punkt Punkt ten dzieli odcinek w stosunku gdyż z twierdzenia Talesa wynika, że
Zobacz też
Przypisy
- ↑ a b Talesa twierdzenie, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2021-07-30].
- ↑ a b c d Twierdzenie Talesa [online], Naukowiec.org [dostęp 2017-06-25] (pol.).
- ↑ a b c d e Twierdzenie Talesa [online], www.math.edu.pl [dostęp 2017-06-25].
Linki zewnętrzne
- Media Nauka, Media Nauka – portal naukowy [online] [dostęp 2017-06-25] (pol.).



































![{\displaystyle [ABC]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdb6e0eac43c0957f7bac6cea97995264c14e92a)




![{\displaystyle {\frac {|CE|}{|EA|}}={\frac {[CED]}{[EAD]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f0b45d4fca090f666a9f09eb4a872fbfed327ef)



![{\displaystyle [CED]=[BDE],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd2bf41dbe6cc7ae9cf8b2106b57a74e490ae166)
![{\displaystyle {\frac {[CED]}{[EAD]}}={\frac {[BDE]}{[EAD]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f270d2afdd4b62e54e0b315907b9fdcb27db988)
![{\displaystyle {\frac {[BDE]}{[EAD]}}={\frac {|BD|}{|DA|}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b0343c33e56b46a33848fe6a0c8f63bf8c81754)
![{\displaystyle {\frac {|CE|}{|EA|}}={\frac {[CED]}{[EAD]}}={\frac {[BDE]}{[EAD]}}={\frac {|BD|}{|DA|}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee9b266f36ca2ccbfe7d538d91cedcc6718ad012)













