Rzut (algebra liniowa)
Rzut lub projekcja[a] – uogólnienie pojęcia rzutu znanego z geometrii elementarnej: idempotentny endomorfizm liniowy określony na danej przestrzeni liniowej, czyli operator liniowy zachowujący swój obraz, tzn. dla którego każdy element obrazu jest punktem stałym tego przekształcenia.
Rzuty/projekcje ortogonalne są uogólnieniem pojęcia rzutu prostokątnego z geometrii euklidesowej (zob. osobna sekcja); w przestrzeniach unitarnych (tzn. z iloczynem skalarnym, np. przestrzeniach euklidesowych) są to nie mniej, nie więcej operatory samosprzężone.
Rzut ukośny
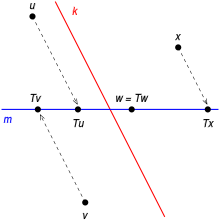
Niech dana będzie przestrzeń liniowa (nad ustalonym ciałem). Przekształcenie liniowe tej przestrzeni w siebie spełniające warunek idempotentności
czyli dla każdego nazywa się rzutem (ukośnym) lub projekcją.
Odwzorowanie można scharakteryzować w następujący sposób: dowolny wektor można przedstawić w jednoznaczny sposób w postaci sumy gdzie oraz [b]. Oznacza to, że czyli jest sumą prostą jądra i obrazu Jeżeli jest skończeniewymiarowa, zaś jest jej podprzestrzenią liniową, to na mocy twierdzenia o rzędzie istnieje rzut dla którego (jeśli to rzutów określonych na o obrazie jest nieskończenie wiele).
Dla danych podprzestrzeni przestrzeni spełniających przekształcenie nazywa się rzutem na wzdłuż jeśli dla każdego zachodzi
- oraz
Jedynymi wartościami własnymi rzutu są zero i jedynka, tzn. widmo rzutu jest równe [c]; ponadto rzut jest diagonalizowalny i w szczególności (w ciele charakterystyki zerowej) jego ślad jest równy wymiarowi obrazu[d]. Z drugiej strony, jeśli przekształcenie ma widmo i jest diagonalizowalne, to jest rzutem[e].
Jeśli jest rzutem na wzdłuż to przekształcenie dane wzorem jest rzutem na wzdłuż [f]. Tym samym rozkładowi odpowiada para rzutów
Rzut ortogonalny
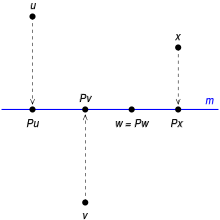
Jeżeli jest rzutem (ukośnym) na wzdłuż oraz jest ortogonalną sumą prostą, to nazywa się rzutem ortogonalnym (na wzdłuż ). Wówczas jest dopełnieniem ortogonalnym czyli zachodzi a więc gdyż wtedy gdzie oraz oznaczają odpowiednio obraz i jądro rzutu
Konstrukcja ortogonalnej sumy prostej wymaga istnienia (niezdegenerowanej) symetrycznej formy dwuliniowej określonej na przestrzeni (tzw. przestrzeń ortogonalna): zwykle rozważa się przestrzenie z iloczynem skalarnym (tzw. przestrzenie unitarne); w przypadku przestrzeni nieskończonego wymiaru zakłada się dodatkowo zupełność, co sprawia, że przestrzeń unitarna staje się przestrzenią Hilberta – istnienie zapewnia wtedy twierdzenie o rzucie ortogonalnym. W tym kontekście rzut ukośny nazywa się operatorem idempotentnym, a rzut ortogonalny znany jest jako operator rzutowy.
Rzut jest ortogonalny wtedy i tylko wtedy, gdy jest i) samosprzężony[g] lub ii) normalny lub iii) dodatni (dodatnio określony) lub iv) izometryczny. Rzuty ortogonalne są operatorami ograniczonymi (czyli ciągłymi), a gdy są nietrywialne: o jednostkowej normie operatorowej[h]; z drugiej strony ograniczony (równoważnie: ciągły) operator liniowy na przestrzeni Hilberta jest rzutem ortogonalnym wtedy i tylko wtedy, gdy
- Gdy rozważana przestrzeń jest zespolona, gwiazdkę przy oznaczeniu macierzy należy interpretować jako sprzężenie hermitowskie, w pozostałych przypadkach – jako transpozycję; w przypadku przekształceń gwiazdka oznacza (antyliniowe) przekształcenie sprzężone do danego.
Jeśli jest bazą ortonormalną podprzestrzeni zaś oznacza macierz typu której kolumnami są to macierz rzutu ortogonalnego dana jest wzorem
i reprezentuje ona przekształcenie, które można zapisać jako[i]
W szczególności rzut na prostą (przestrzeń jednowymiarową) rozpinaną przez wektor jednostkowy dany jest wzorem a jego macierz ma postać [j].
Macierz reprezentuje izometrię częściową która znika na dopełnieniu ortogonalnym podprzestrzeni zaś jest izometrią, która zanurza w przestrzeń
Warunek ortonormalności można opuścić; jeżeli jest bazą (niekoniecznie ortonormalną), a macierz zawiera te wektory jako kolumny, to rzut ma postać[k]
Reprezentowane przez tę macierz przekształcenie nadal zanurza w przestrzeń jednak nie musi być już izometrią.
Przykłady
- Przekształcenie tożsamościowe jest rzutem ortogonalnym reprezentowanym przez macierz jednostkową, np. (operator jednostkowy jest operatorem rzutowym).
- Przekształcenie liniowe, którego macierz ma postać jest rzutem ortogonalnym, podczas gdy zadane macierzą jest rzutem (ukośnym), ale nie ortogonalnym (pierwsza macierz opisuje operator rzutowy, druga – tylko idempotentny).
- Przestrzeń funkcji rzeczywistych całkowalnych z kwadratem (w sensie Lebesgue’a) jest ortogonalną sumą prostą przestrzeni funkcji parzystych i nieparzystych; rzuty odpowiednio na dane są wzorami[l]
- przy czym
- Niech będzie zbiorem mierzalnym np. przedziałem, z funkcją charakterystyczną Wówczas[l] jest rzutem ortogonalnym na podprzestrzeń funkcji o nośniku zawartym w domknięciu
- Zamiast wspomnianej wcześniej przestrzeni Hilberta z operatorem można rozważać inne: w przypadku przestrzeni ciągów gdy gdzie [m], oraz to rzut przyjmuje postać
- Jeśli z kolei dana jest przestrzeń jest przestrzenią funkcji o okresie [n], a jest funkcją stałą o jednostkowej normie, to rzut ortogonalny przekształca funkcję w jej średnią gdzie
- Odpowiadający temu rzutowi rozkład ortogonalny, rozbija funkcję na stałą część średnią i zmienną część o zerowej średniej.
- Stosowany w matematycznym opisie mechaniki kwantowej operator liczby cząstek dla fermionów jest operatorem rzutowym.
Uwagi
- ↑ Etymologia w artykule projekcja.
- ↑ Wystarczy przyjąć oraz wtedy
- ↑ Niech będzie wektorem własnym stowarzyszonym z wartością własną rzutu Wówczas
- ↑ Niech będą bazą Wówczas zakładając, że otrzymuje się zatem dowolny niezerowy wektor w obrazie jest wektorem własnym z wartością własną W ten sposób wymiar przestrzeni własnej dla wartości własnej jest niemniejszy niż rząd Z twierdzenia o rzędzie wynika jednak, że (gdyż ) dlatego suma wymiarów dwóch podprzestrzeni jest równa wymiarowi całej przestrzeni Bazy obrazu i jądra tworzą razem bazę wektorów własnych tzn. stąd jest diagonalizowalny i wymiar przestrzeni własnej dla wartości własnej jest równy rzędowi Ponieważ ślad jest sumą wartości własnych (w ciele charakterystyki 0), to
- ↑ Jeśli gdzie jest jednokładnością (tj. przekształceniem, którego macierz jest macierzą diagonalną) wyłącznie z wartościami własnymi równymi zeru lub jedynce (na przekątnej głównej), to
- ↑ Z bezpośredniego rachunku wynika, że
- ↑ Wychodząc od samosprzężoności i idempotentności oraz dowolnych wektorów otrzymuje się oraz
- ↑ Dla dowolnego wektora z nierówności Cauchy’ego–Schwarza jest
- ↑ W notacji Diraca jest
- ↑ Wtedy W stosowanej głównie w fizyce notacji Diraca jest wówczas W matematyce zwykle zapisuje się za pomocą iloczynu tensorowego (a dokładnie: iloczynu diadycznego).
- ↑ Macierz jest „czynnikiem normującym”, który odzyskuje normę: operator pierwszego rzędu jest rzutem, tylko gdy dzieląc przez otrzymuje się rzut na podprzestrzeń
- ↑ a b Oznaczenia należy rozumieć jako gdzie jest operatorem, którego argumenty i wartości są funkcjami z przestrzeni tzn. dla pewnej podprzestrzeni przestrzeni
- ↑ Zob. delta Kroneckera
- ↑ Por. grupa okręgu
Bibliografia
- F.W. Gehring, P.R. Halmos, C.C Moore: A Course in Functional Analysis. Nowy Jork: Springer-Verlag, 1985.
Linki zewnętrzne
![]() Paweł Lubowiecki, nagrania na YouTube, Wojskowa Akademia Techniczna im. Jarosława Dąbrowskiego, kanał „Uczelnia WAT”, 30 stycznia 2024 [dostęp 2024-09-09]:
Paweł Lubowiecki, nagrania na YouTube, Wojskowa Akademia Techniczna im. Jarosława Dąbrowskiego, kanał „Uczelnia WAT”, 30 stycznia 2024 [dostęp 2024-09-09]:























































![{\displaystyle \left[{\begin{smallmatrix}1&0\\0&1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/765b8147864544b36f917d90fe67728dcd47417f)
![{\displaystyle \left[{\begin{smallmatrix}1&0\\0&0\end{smallmatrix}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef2e796a45d3fe43bc85fc38cff53215da6c0ee8)
![{\displaystyle \left[{\begin{smallmatrix}0&1\\0&1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdc7bb80e487b6a387428e7d48596867cfc35b2d)































































































