Liczby bliźniacze
Liczby bliźniacze – dwie liczby pierwsze, których różnica wynosi 2[1], np.: 3 i 5, 5 i 7, 11 i 13.
Skończoność zbioru par liczb bliźniaczych
Do dzisiaj nie wiadomo, czy liczb bliźniaczych jest nieskończenie wiele, jak sugeruje hipoteza o liczbach pierwszych bliźniaczych.
W 1919 roku norweski matematyk Viggo Brun udowodnił, że szereg odwrotności liczb bliźniaczych jest zbieżny[2]:
Własności liczb bliźniaczych
- Liczba 5 jest bliźniacza zarówno z 3, jak i z 7. Nie istnieje inna liczba pierwsza bliźniacza z dwiema liczbami.
- Dowód:
- Istnieją trzy możliwe przypadki ciągu liczb naturalnych o różnicy 2 dla naturalnego: lub W każdym z nich jest jedna liczba podzielna przez 3: odpowiednio: i Oznacza to, że aby w ciągu trzech liczb naturalnych wszystkie były pierwsze, jedna z nich musi być równa 3. Istnieją dwa takie ciągi: i lecz 1 z definicji nie jest liczbą pierwszą.
- Największe znane dziś liczby bliźniacze, każda składająca się z 388 342 cyfr, to 2996863034895·21290000 ± 1 znalezione w 2016 roku[3],
- Z wyjątkiem par 3 i 5 oraz 5 i 7, ostatnimi cyframi liczb bliźniaczych mogą być: 1 i 3 (na przykład 11 i 13), 7 i 9 (na przykład 17 i 19) oraz 9 i 1 (na przykład 29 i 31).
- Dla każdej pary liczb bliźniaczych większych lub równych 5, liczba naturalna między nimi (rozdzielająca parę) jest podzielna przez 6. Wynika to z faktu, że jest ona parzysta i ponieważ w każdej trójce kolejnych liczb jest liczba podzielna przez trzy (bo dwie pozostałe są pierwsze), to mamy również podzielność przez iloczyn liczb dwa i trzy.
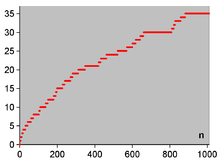
Wszystkie liczby bliźniacze do 2000
|
|
|
|
Przypisy
- ↑ liczby bliźniacze, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2021-09-30].
- ↑ Enumeration to 1.6e15 of the twin primes and Brun’s constant. trnicely.net. [zarchiwizowane z tego adresu (2013-12-08)]. (ang.).
- ↑ The Ten Largest Known Twin Primes.
Bibliografia
- Lidia Filist, Artur Malina, Alicja Solecka: Słownik matematyczny. Wrocław: Wydawnictwo Europa, 2005, s. 150. ISBN 83-88962-41-8.
Linki zewnętrzne
- Eric W. Weisstein, Twin Primes, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2022-07-02].










