In geometry, a Grünbaum–Dress polyhedron is a regular skeletal polyhedron. A skeletal polyhedron has faces which, like an ordinary polyhedron. are polygonal circuits of edges and vertices but which, unlike an ordinary one, have no interior and need not be planar. A regular polyhedron is one whose symmetries are transitive on its flags.

Skeletal polyhedra have appeared in the literature at least since the Italian Renaissance. In 1509 Leonardo da Vinci drew illustrations of several to illustrate Luca Pacioli's book De Divina Proportione ("On Divine Proportion"). Their mathematical significance was first studied in the mid-twentieth century by Branko Grünbaum, who intially referred to them as polyhedra with hollow faces.^[1]

They led to new classes of regular polyhedra which he listed in 1979.^[2] Andreas Dress noticed an omission and enumerated a more complete list in 1985.^[3] The regular skeletal polyhedra have since become known as the Grünbaum-Dress polyhedra.^[4][5]

In 1994 Grünbaum extended the idea to less regular polyhedra^[1] and in 2016 Egon Schulte and Abigail Williams explored uniform skeletal polyhedra.^[6]

• Saddle polyhedron: If the faces are filled in, with for example minimal surfaces, the figure is instead known as a saddle polyhedron.^[7]

• E. Schulte; "Symmetry of Polytopes and Polyhedra". In: Jacob E. Goodman and Joseph O'Rourke (eds.); Handbook of Discrete and Computational Geometry, Second Edition, Chapman & Hall, 2004, Chapter 19, Section 19.4, pp.439-441. (Also as Section 18.4 in the First Edition and Third Edition 18.4 The Grünbaum-Dress Polyhedra).
• P. McMullen and E. Schulte; "Regular Polytopes in Ordinary Space", Discrete & Computational Geometry, Vol 17, Issue 4, June 1997, pp.449–478. [Abstract: The three aims of this paper are to obtain the proof by Dress of the completeness of the enumeration of the Grünbaum—Dress polyhedra (that is, the regular apeirohedra, or apeirotopes of rank 3) in ordinary space E³ in a quicker and more perspicuous way, to give presentations of those of their symmetry groups which are affinely irreducible, and to describe all the discrete regular apeirotopes of rank 4 in E³. The paper gives a complete classification of the discrete regular polytopes in ordinary space.]

• Skeletal regular polyhedron is currently an orphan and redirects to Steinitz's theorem.
• Saddle polyhedra can have twofold vertices (digon-al vertex figures), which are not allowed by Grünbaum & Dress.

Reflections concerning triply-periodic minimal surfaces Alan H. Schoen Interface Focus (2012) Vol.2, 658–668 Refs Pearce calling them "Saddle polyhedra", & does so too. "In recent years, several authors [26,27] have applied Delaney–Dress tiling theory to formalize the concept of saddle polyhedra. Nice pix.
"26 Delgado-Friedrichs, O., O’Keeffe, M. & Yaghi, O. M. 2003 Three-periodic nets and tillings: regular and quasiregular nets.Acta Cryst. A59, 22–27.
"27 Bonneau, C., Delgado-Friedrichs, O., O’Keeffe, M. & Yaghi, O. M. 2004 Three-periodic nets and tillings: minimal nets. Acta Cryst. A60, 517–520." https://royalsocietypublishing.org/doi/pdf/10.1098/rsfs.2012.0023

http://gerdschroeder-turk.org/wp-content/uploads/2015/06/SchroederHyde_PDStarblock_Helix91_2003.pdf Namechecks sadle polyhedron in caption to 1st image. Discusses Pearce as first to study/name them.

S.D. Hyde; Sponges. In Foams and Emulsions, Springer 1999. edited by J.F. Sadoc, N. Rivier, Chapter XXVI, pp.437-470 [ref. p.466] https://books.google.co.uk/books?id=9avzCAAAQBAJ&pg=PA466&lpg=PA466

Yu.D. Burago and S.Z. Shefel'; Chapter 3: saddle Surfaces. In Geometry III: Theory of Surfaces, edited by Yu.D. Burago, V.A. Zalgaller. https://books.google.co.uk/books?id=23jpCAAAQBAJ [no df of saddle polyhedron apparent.

Probably at best a section in either the torus or fractal articles.

A fractal torus is a torus or donut shape which has scale-independent or fractal properties. The term has been used informally for several different constructions:

A recursive toroidal form

built up from smaller toroids or loops, themselves built up from yet smaller loops still, and so on. May be discrete rings or a single interconnected fractal spiral.

• The Torus - Dynamic Flow Process, Cosmometry
• How to Create a Fractal Torus, Sti's Blog.

In chaos theory

A roughened, fractal toroidal surface, intermediate between wrinkled and broken or disjoint.

• Nikola Samardzija & Larry D. Greller; "Explosive route to chaos through a fractal torus in a generalized Lotka-Volterra model", Bulletin of Mathematical Biology, Volume 50, Issue 5, September 1988, pp 465–491.
• Ali H. Nayfeh & Balakumar Balachandran; Applied Nonlinear Dynamics: Analytical, Computational, and Experimental Methods, Wiley 1995.
• Steinmetz, C. G. & Larter, R.; "The quasiperiodic route to chaos in a model of the peroxidase-oxidase reaction", J. Chem. Phys. Vol. 94, 1991, pp.1388-1396.

Topology

A realization of a locally-flat (isometric) torus in 3-space where the tangent plane is defined everywhere, but the normal vector is not defined, so it’s also a fractal. See Torus#Flat torus.

• Evelyn lamb; "A Few of My Favorite Spaces: The Torus", Scientific American blog, 28 November, 2015
• Jacob Aron; Wrinkled doughnut solves geometrical mystery, New Scientist, 5 May 2012.
• Vincent Borrelli, Saïd Jabrane, Francis Lazarus and Boris Thibert; "Flat tori in three-dimensional space and convex integration", PNAS, 2012.

Informally

A fractal pattern or arbitrary kind imposed on a toroidal surface.

[nothing even faintly resembling an RS yet]

To continue Polyhedron#Convex polyhedra

The sum of the exterior angles of any convex polygon equals 2π radians (360 degrees). This is [sometimes? - see Talk:Exterior angle theorem] known as the exterior angle theorem. The exterior angle at a corner can be seen as the difference or defect between a straight line and the interior angle. The sum of the exterior angles is just the sum of these angle defects.<Richeson, D.; Euler's Gem: The Polyhedron Formula and the Birth of Topology, Princeton (2008), Page 220.>

Convex polyhedra have an analogous angle defect. At each vertex, the face angles of a convex polyhedron always sum to less than 2π. The sum of these angle defects for every vertex is always equal to 4π radians (720 degrees).<Coxeter, Regular Polytopes. Page 23.><Richeson (2008), Page 223-225.>

To continue Polyhedron#Topological characteristics

[See Richeson, as above and ff.]

From Uniform polytope

Related to the subject of finite uniform polytopes are uniform honeycombs in Euclidean and hyperbolic spaces. Euclidean uniform honeycombs are generated by affine Coxeter groups and hyperbolic honeycombs are generated by the hyperbolic Coxeter groups. Two affine Coxeter groups can be multiplied together.

There are two classes of hyperbolic Coxeter groups, compact and paracompact. Uniform honeycombs generated by compact groups have finite facets and vertex figures, and exist in 2 through 4 dimensions. Paracompact groups have affine or hyperbolic subgraphs, and infinite facets or vertex figures, and exist in 2 through 10 dimensions.

From Honeycomb (geometry)

A uniform honeycomb is a honeycomb in Euclidean 3-space composed of uniform polyhedral cells, and having all vertices the same (i.e., the group of [isometries of 3-space that preserve the tiling] is transitive on vertices). There are 28 convex examples,^[1] also called the Archimedean honeycombs.

A honeycomb is called regular if the group of isometries preserving the tiling acts transitively on flags, where a flag is a vertex lying on an edge lying on a face lying on a cell. Every regular honeycomb is automatically uniform. However, there is just one regular honeycomb in Euclidean 3-space, the cubic honeycomb. Two are quasiregular (made from two types of regular cells):

Type	Regular cubic honeycomb	Quasiregular honeycombs
Cells	Cubic	Octahedra and tetrahedra
Slab layer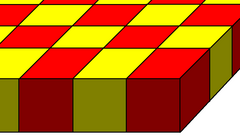
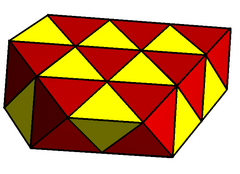
Slab construction	= {}×{4,4}	= s{2,6,3}

The tetrahedral-octahedral honeycomb and gyrated tetrahedral-octahedral honeycombs are generated by 3 or 2 positions of slab layer of cells, each alternating tetrahedra and octahedra. An infinite number of unique honeycombs can be created by higher order of patterns of repeating these slab layers.