Tetrahedral prism
Schlegel diagram
Type	Prismatic uniform 4-polytope
Uniform index	48
Schläfli symbol	t{2,3,3} = {}×{3,3} = h{4,3}×{} s{2,4}×{} sr{2,2}×{}
Coxeter diagram	=
Cells	2 (3.3.3) 4 (3.4.4)
Faces	8 {3} 6 {4}
Edges	16
Vertices	8
Vertex configuration	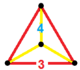Equilateral-triangular pyramid
Dual	Tetrahedral bipyramid
Symmetry group	[3,3,2], order 48 [4,2+,2], order 16 [(2,2)+,2], order 8
Properties	convex
Net

In geometry, a tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 6 polyhedral cells: 2 tetrahedra connected by 4 triangular prisms. It has 14 faces: 8 triangular and 6 square. It has 16 edges and 8 vertices.

It is one of 18 uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids and Archimedean solids.

An orthographic projection showing the pair of parallel tetrahedra projected as a quadrilateral divided into yellow and blue triangular faces. Each tetrahedra also have two other uncolored triangles across the opposite diagonal.

Transparent Schlegel diagram seen as one tetrahedron nested inside another, with 4 triangular prisms between pairs of triangular faces.

Rotating on 2 different planes

1. Tetrahedral dyadic prism (Norman W. Johnson)
2. Tepe (Jonathan Bowers: for tetrahedral prism)
3. Tetrahedral hyperprism
4. Digonal antiprismatic prism
5. Digonal antiprismatic hyperprism

The tetrahedral prism is bounded by two tetrahedra and four triangular prisms. The triangular prisms are joined to each other via their square faces, and are joined to the two tetrahedra via their triangular faces.

The tetrahedron-first orthographic projection of the tetrahedral prism into 3D space has a tetrahedral projection envelope. Both tetrahedral cells project onto this tetrahedron, while the triangular prisms project to its faces.

The triangular-prism-first orthographic projection of the tetrahedral prism into 3D space has a projection envelope in the shape of a triangular prism. The two tetrahedral cells are projected onto the triangular ends of the prism, each with a vertex that projects to the center of the respective triangular face. An edge connects these two vertices through the center of the projection. The prism may be divided into three non-uniform triangular prisms that meet at this edge; these 3 volumes correspond with the images of three of the four triangular prismic cells. The last triangular prismic cell projects onto the entire projection envelope.

The edge-first orthographic projection of the tetrahedral prism into 3D space is identical to its triangular-prism-first parallel projection.

The square-face-first orthographic projection of the tetrahedral prism into 3D space has a cuboidal envelope (see diagram). Each triangular prismic cell projects onto half of the cuboidal volume, forming two pairs of overlapping images. The tetrahedral cells project onto the top and bottom square faces of the cuboid.

It is the first in an infinite series of uniform antiprismatic prisms.

Convex p-gonal antiprismatic prisms

Name	s{2,2}×{}	s{2,3}×{}	s{2,4}×{}	s{2,5}×{}	s{2,6}×{}	s{2,7}×{}	s{2,8}×{}	s{2,p}×{}
Coxeter diagram
Image
Vertex figure
Cells	2 s{2,2} (2) {2}×{}={4} 4 {3}×{}	2 s{2,3} 2 {3}×{} 6 {3}×{}	2 s{2,4} 2 {4}×{} 8 {3}×{}	2 s{2,5} 2 {5}×{} 10 {3}×{}	2 s{2,6} 2 {6}×{} 12 {3}×{}	2 s{2,7} 2 {7}×{} 14 {3}×{}	2 s{2,8} 2 {8}×{} 16 {3}×{}	2 s{2,p} 2 {p}×{} 2p {3}×{}
Net

The tetrahedral prism, -1₃₁, is first in a dimensional series of uniform polytopes, expressed by Coxeter as k₃₁ series. The tetrahedral prism is the vertex figure for the second, the rectified 5-simplex. The fifth figure is a Euclidean honeycomb, 3₃₁, and the final is a noncompact hyperbolic honeycomb, 4₃₁. Each uniform polytope in the sequence is the vertex figure of the next.

k₃₁ dimensional figures

n	4	5	6	7	8	9
Coxeter group	A3A1	A5	D6	E7	= E7+	=E7++
Coxeter diagram
Symmetry	[3−1,3,1]	[30,3,1]	[31,3,1]	[32,3,1]	[33,3,1]	[34,3,1]
Order	48	720	23,040	2,903,040	∞
Graph					-	-
Name	−131	031	131	231	331	431

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
• Norman Johnson Uniform Polytopes, Manuscript (1991)

• 6. Convex uniform prismatic polychora - Model 48, George Olshevsky.
• Klitzing, Richard. "4D uniform polytopes (polychora) x x3o3o - tepe".