Template:Infobox mathematical function
| name | |
|---|---|
| [[File:{{{image}}}|frameless]] | |
| Domain, codomain and image | |
| Domain | domain |
| Codomain | codomain |
| Image | range |
| Basic features | |
| Parity | parity |
| Period | period |
| Specific values | |
| At zero | zero |
| Value at +∞ | plusinf |
| Value at −∞ | minusinf |
| Maxima | max |
| Minima | min |
| Value at vr1 | f1 |
| Value at vr2 | f2 |
| Value at [...] | [...] |
| Value at vr5 | f5 |
| Specific features | |
| Asymptote | asymptote |
| Root | root |
| Critical point | critical |
| Inflection point | inflection |
| Fixed point | fixed |
notes | |
Blank syntax
{{Infobox mathematical function
| name =
| image= |imagesize= <!--(default 220px)--> |imagealt=
| parity= |domain= |codomain= |range= |period=
| zero= |plusinf= |minusinf= |max= |min=
| vr1= |f1= |vr2= |f2= |vr3= |f3= |vr4= |f4= |vr5= |f5=
| asymptote= |root= |critical= |inflection= |fixed=
| notes =
}}
Parameters
- Pairs VR1-f1, f1-VR2, etc. are used for labeling specific value functions. Suppose a function at the point e has a value of 2e and that this point is because of something specific. In this case you should put that as VR1 = eand f1 = 2e. For the next point is used a couple of VR2-f2, etc. If you run out of points (five currently available), ask for more.
- Variables heading1, heading2, heading3 define whether some of the headlines basic properties, specific values, etc. be displayed. If you do not want a title to be displayed, simply delete the variable from the template. Set the value of the variable to 0 or anything will not prevent the display title.
- Variables plusinf and minusinf indicate the value function at + ∞ and - ∞.
- root is the x-intercept, critical is the critical point(s), inflection is inflection point(s)
- fixed is fixed point(s)
Example
The code below produces the box opposite:
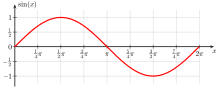
| Sine | |
|---|---|
 | |
| General information | |
| General definition | |
| Motivation of invention | Indian astronomy |
| Date of solution | Gupta period |
| Fields of application | Trigonometry, Integral transform, etc. |
| Domain, codomain and image | |
| Domain | (−∞, +∞) a |
| Image | [−1, 1] a |
| Basic features | |
| Parity | odd |
| Period | 2π |
| Specific values | |
| At zero | 0 |
| Maxima | (2kπ + π/2, 1)b |
| Minima | (2kπ − π/2, −1) |
| Specific features | |
| Root | kπ |
| Critical point | kπ + π/2 |
| Inflection point | kπ |
| Fixed point | 0 |
| Related functions | |
| Reciprocal | Cosecant |
| Inverse | Arcsine |
| Derivative | |
| Antiderivative | |
| Other Related | cos, tan, csc, sec, cot |
| Series definition | |
| Taylor series | |
| Generalized continued fraction | |
| Gamma | |
|---|---|
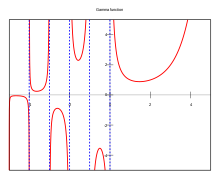 The gamma function along part of the real axis | |
| General information | |
| General definition | , |
| Deriver of General definition | Daniel Bernoulli |
| Motivation of invention | Interpolation for factorial function |
| Date of solution | 1720s |
| Extends | Factorial function |
| Fields of application | Probability, statistics, combinatorics |
| Main applications | probability-distribution functions |
| Domain, codomain and image | |
| Domain | - ℤ0- |
| Image | |
| Basic features | |
| Parity | Not even and not odd |
| Period | No |
| Analytic? | Yes |
| Meromorphic? | Yes |
| Holomorphic? | Yes except at ℤ0- |
| Specific values | |
| Maxima | No |
| Minima | No |
| Value at ℤ+ | |
| Value at ℤ0- | Not defined |
| Specific features | |
| Root | No |
| Critical point | ℤ0- |
| Inflection point | ℤ0- |
| Fixed point | 1 |
| Poles | ℤ0- |
| Transform | |
| Corresponding transform | Mellin transform |
| Corresponding transform formula | |
{{Infobox mathematical function
| name = Sine
| image = Sinus.svg
| parity=odd |domain=(-∞,∞) |range=[-1,1] |period=2π
| zero=0 |plusinf= |minusinf= |max=((2k+½)π,1) |min=((2k-½)π,-1)
| asymptote= |root=kπ |critical=kπ-π/2 |inflection=kπ |fixed=0
| notes = Variable k is an [[integer]].
}}




![{\displaystyle {\begin{aligned}x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[8pt]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}\\[8pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91b7e722b0e78f16453f0b08592125448c3a0d8e)







