Langbahn Team – Weltmeisterschaft

Stericated 6-cubes


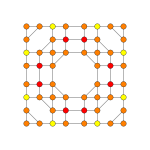
6-cube
Stericated 6-cube
Steritruncated 6-cube

Stericantellated 6-cube
Stericantitruncated 6-cube
Steriruncinated 6-cube

Steriruncitruncated 6-cube
Steriruncicantellated 6-cube
Steriruncicantitruncated 6-cube
Orthogonal projections in B6 Coxeter plane

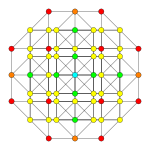
In six-dimensional geometry, a stericated 6-cube is a convex uniform 6-polytope, constructed as a sterication (4th order truncation) of the regular 6-cube.

There are 8 unique sterications for the 6-cube with permutations of truncations, cantellations, and runcinations.

Stericated 6-cube

Stericated 6-cube
Type uniform 6-polytope
Schläfli symbol 2r2r{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges 5760
Vertices 960
Vertex figure
Coxeter groups B6, [4,3,3,3,3]
Properties convex

Alternate names

  • Small cellated hexeract (Acronym: scox) (Jonathan Bowers)[1]

Images

orthographic projections
Coxeter plane B6 B5 B4
Graph
Dihedral symmetry [12] [10] [8]
Coxeter plane B3 B2
Graph
Dihedral symmetry [6] [4]
Coxeter plane A5 A3
Graph
Dihedral symmetry [6] [4]

Steritruncated 6-cube

Steritruncated 6-cube
Type uniform 6-polytope
Schläfli symbol t0,1,4{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges 19200
Vertices 3840
Vertex figure
Coxeter groups B6, [4,3,3,3,3]
Properties convex

Alternate names

  • Cellirhombated hexeract (Acronym: catax) (Jonathan Bowers)[2]

Images

orthographic projections
Coxeter plane B6 B5 B4
Graph
Dihedral symmetry [12] [10] [8]
Coxeter plane B3 B2
Graph
Dihedral symmetry [6] [4]
Coxeter plane A5 A3
Graph
Dihedral symmetry [6] [4]

Stericantellated 6-cube

Stericantellated 6-cube
Type uniform 6-polytope
Schläfli symbol 2r2r{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges 28800
Vertices 5760
Vertex figure
Coxeter groups B6, [4,3,3,3,3]
Properties convex

Alternate names

  • Cellirhombated hexeract (Acronym: crax) (Jonathan Bowers)[3]

Images

orthographic projections
Coxeter plane B6 B5 B4
Graph
Dihedral symmetry [12] [10] [8]
Coxeter plane B3 B2
Graph
Dihedral symmetry [6] [4]
Coxeter plane A5 A3
Graph
Dihedral symmetry [6] [4]

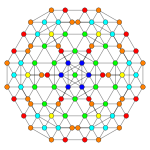
Stericantitruncated 6-cube

stericantitruncated 6-cube
Type uniform 6-polytope
Schläfli symbol t0,1,2,4{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges 46080
Vertices 11520
Vertex figure
Coxeter groups B6, [4,3,3,3,3]
Properties convex

Alternate names

  • Celligreatorhombated hexeract (Acronym: cagorx) (Jonathan Bowers)[4]

Images

orthographic projections
Coxeter plane B6 B5 B4
Graph
Dihedral symmetry [12] [10] [8]
Coxeter plane B3 B2
Graph
Dihedral symmetry [6] [4]
Coxeter plane A5 A3
Graph
Dihedral symmetry [6] [4]

Steriruncinated 6-cube

steriruncinated 6-cube
Type uniform 6-polytope
Schläfli symbol t0,3,4{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges 15360
Vertices 3840
Vertex figure
Coxeter groups B6, [4,3,3,3,3]
Properties convex

Alternate names

  • Celliprismated hexeract (Acronym: copox) (Jonathan Bowers)[5]

Images

orthographic projections
Coxeter plane B6 B5 B4
Graph
Dihedral symmetry [12] [10] [8]
Coxeter plane B3 B2
Graph
Dihedral symmetry [6] [4]
Coxeter plane A5 A3
Graph
Dihedral symmetry [6] [4]

Steriruncitruncated 6-cube

steriruncitruncated 6-cube
Type uniform 6-polytope
Schläfli symbol 2t2r{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges 40320
Vertices 11520
Vertex figure
Coxeter groups B6, [4,3,3,3,3]
Properties convex

Alternate names

  • Celliprismatotruncated hexeract (Acronym: captix) (Jonathan Bowers)[6]

Images

orthographic projections
Coxeter plane B6 B5 B4
Graph
Dihedral symmetry [12] [10] [8]
Coxeter plane B3 B2
Graph
Dihedral symmetry [6] [4]
Coxeter plane A5 A3
Graph
Dihedral symmetry [6] [4]

Steriruncicantellated 6-cube

steriruncicantellated 6-cube
Type uniform 6-polytope
Schläfli symbol t0,2,3,4{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges 40320
Vertices 11520
Vertex figure
Coxeter groups B6, [4,3,3,3,3]
Properties convex

Alternate names

  • Celliprismatorhombated hexeract (Acronym: coprix) (Jonathan Bowers)[7]

Images

orthographic projections
Coxeter plane B6 B5 B4
Graph
Dihedral symmetry [12] [10] [8]
Coxeter plane B3 B2
Graph
Dihedral symmetry [6] [4]
Coxeter plane A5 A3
Graph
Dihedral symmetry [6] [4]

Steriruncicantitruncated 6-cube

Steriuncicantitruncated 6-cube
Type uniform 6-polytope
Schläfli symbol tr2r{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges 69120
Vertices 23040
Vertex figure
Coxeter groups B6, [4,3,3,3,3]
Properties convex

Alternate names

  • Great cellated hexeract (Acronym: gocax) (Jonathan Bowers)[8]

Images

orthographic projections
Coxeter plane B6 B5 B4
Graph
Dihedral symmetry [12] [10] [8]
Coxeter plane B3 B2
Graph
Dihedral symmetry [6] [4]
Coxeter plane A5 A3
Graph
Dihedral symmetry [6] [4]

These polytopes are from a set of 63 uniform 6-polytopes generated from the B6 Coxeter plane, including the regular 6-cube or 6-orthoplex.

B6 polytopes

β6
t1β6
t2β6
t2γ6
t1γ6
γ6
t0,1β6
t0,2β6

t1,2β6
t0,3β6
t1,3β6
t2,3γ6
t0,4β6
t1,4γ6
t1,3γ6
t1,2γ6

t0,5γ6
t0,4γ6
t0,3γ6
t0,2γ6
t0,1γ6
t0,1,2β6
t0,1,3β6
t0,2,3β6

t1,2,3β6
t0,1,4β6
t0,2,4β6
t1,2,4β6
t0,3,4β6
t1,2,4γ6
t1,2,3γ6
t0,1,5β6

t0,2,5β6
t0,3,4γ6
t0,2,5γ6
t0,2,4γ6
t0,2,3γ6
t0,1,5γ6
t0,1,4γ6
t0,1,3γ6

t0,1,2γ6
t0,1,2,3β6
t0,1,2,4β6
t0,1,3,4β6
t0,2,3,4β6
t1,2,3,4γ6
t0,1,2,5β6
t0,1,3,5β6

t0,2,3,5γ6
t0,2,3,4γ6
t0,1,4,5γ6
t0,1,3,5γ6
t0,1,3,4γ6
t0,1,2,5γ6
t0,1,2,4γ6
t0,1,2,3γ6

t0,1,2,3,4β6
t0,1,2,3,5β6
t0,1,2,4,5β6
t0,1,2,4,5γ6
t0,1,2,3,5γ6
t0,1,2,3,4γ6
t0,1,2,3,4,5γ6


Notes

  1. ^ Klitzing, (x4o3o3o3x3o - scox)
  2. ^ Klitzing, (x4x3o3o3x3o - catax)
  3. ^ Klitzing, (x4o3x3o3x3o - crax)
  4. ^ Klitzing, (x4x3x3o3x3o - cagorx)
  5. ^ Klitzing, (x4o3o3x3x3o - copox))
  6. ^ Klitzing, (x4x3o3x3x3o - captix)
  7. ^ Klitzing, (x4o3x3x3x3o - coprix)
  8. ^ Klitzing, (x4x3x3x3x3o - gocax)

References

  • H.S.M. Coxeter:
    • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
    • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
      • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
      • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
      • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
  • Norman Johnson Uniform Polytopes, Manuscript (1991)
    • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
  • Klitzing, Richard. "6D uniform polytopes (polypeta)".
Fundamental convex regular and uniform polytopes in dimensions 2–10
Family An Bn I2(p) / Dn E6 / E7 / E8 / F4 / G2 Hn
Regular polygon Triangle Square p-gon Hexagon Pentagon
Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron
Uniform polychoron Pentachoron 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell
Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube
Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221
Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321
Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421
Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube
Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube
Uniform n-polytope n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds
Quelle: https://en.wikipedia.org/wiki/Steriruncinated_6-cube