Stellation

In geometry, stellation is the process of extending a polygon in two dimensions, a polyhedron in three dimensions, or, in general, a polytope in n dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word stellation comes from the Latin stellātus, "starred", which in turn comes from the Latin stella, "star". Stellation is the reciprocal or dual process to faceting.
Kepler's definition
In 1619 Kepler defined stellation for polygons and polyhedra as the process of extending edges or faces until they meet to form a new polygon or polyhedron.
He stellated the regular dodecahedron to obtain two regular star polyhedra, the small stellated dodecahedron and the great stellated dodecahedron. He also stellated the regular octahedron to obtain the stella octangula, a regular compound of two tetrahedra.
Stellating polygons

Stellating a regular polygon symmetrically creates a regular star polygon or polygonal compound. These polygons are characterised by the number of times m that the polygonal boundary winds around the centre of the figure. Like all regular polygons, their vertices lie on a circle. m also corresponds to the number of vertices around the circle to get from one end of a given edge to the other, starting at 1.
A regular star polygon is represented by its Schläfli symbol {n/m}, where n is the number of vertices, m is the step used in sequencing the edges around it, and m and n are coprime (have no common factor). The case m = 1 gives the convex polygon {n}. m also must be less than half of n; otherwise the lines will either be parallel or diverge, preventing the figure from ever closing.
If n and m do have a common factor, then the figure is a regular compound. For example {6/2} is the regular compound of two triangles {3} or hexagram, while {10/4} is a compound of two pentagrams {5/2}.
Some authors use the Schläfli symbol for such regular compounds. Others regard the symbol as indicating a single path which is wound m times around n/m vertex points, such that one edge is superimposed upon another and each vertex point is visited m times. In this case a modified symbol may be used for the compound, for example 2{3} for the hexagram and 2{5/2} for the regular compound of two pentagrams.
A regular n-gon has n – 4/2 stellations if n is even (assuming compounds of multiple degenerate digons are not considered), and n – 3/2 stellations if n is odd.
 The pentagram, {5/2}, is the only stellation of a pentagon. |
 The hexagram, {6/2}, the stellation of a hexagon and a compound of two triangles |
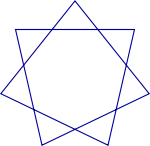
 The enneagon (nonagon) {9} has 3 enneagrammic forms: {9/2}, {9/3}, {9/4}, with {9/3} being a compound of 3 triangles. |
| ||
Like the heptagon, the octagon also has two octagrammic stellations, one, {8/3} being a star polygon, and the other, {8/2}, being the compound of two squares.
Stellating polyhedra

|

|

|

|

|

|

|
A polyhedron is stellated by extending the edges or face planes of a polyhedron until they meet again to form a new polyhedron or compound. The interior of the new polyhedron is divided by the faces into a number of cells. The face planes of a polyhedron may divide space into many such cells, and as the stellation process continues then more of these cells will be enclosed. For a symmetrical polyhedron, these cells will fall into groups, or sets, of congruent cells – we say that the cells in such a congruent set are of the same type. A common method of finding stellations involves selecting one or more cell types.
This can lead to a huge number of possible forms, so further criteria are often imposed to reduce the set to those stellations that are significant and unique in some way.
A set of cells forming a closed layer around its core is called a shell. For a symmetrical polyhedron, a shell may be made up of one or more cell types.
Based on such ideas, several restrictive categories of interest have been identified.
- Main-line stellations. Adding successive shells to the core polyhedron leads to the set of main-line stellations.
- Fully supported stellations. The underside faces of a cell can appear externally as an "overhang." In a fully supported stellation there are no such overhangs, and all visible parts of a face are seen from the same side.
- Monoacral stellations. Literally "single-peaked." Where there is only one kind of peak, or vertex, in a stellation (i.e. all vertices are congruent within a single symmetry orbit), the stellation is monoacral. All such stellations are fully supported.
- Primary stellations. Where a polyhedron has planes of mirror symmetry, edges falling in these planes are said to lie in primary lines. If all edges lie in primary lines, the stellation is primary. All primary stellations are fully supported.
- Miller stellations. In "The Fifty-Nine Icosahedra" Coxeter, Du Val, Flather and Petrie record five rules suggested by Miller. Although these rules refer specifically to the icosahedron's geometry, they have been adapted to work for arbitrary polyhedra. They ensure, among other things, that the rotational symmetry of the original polyhedron is preserved, and that each stellation is different in outward appearance. The four kinds of stellation just defined are all subsets of the Miller stellations.
We can also identify some other categories:
- A partial stellation is one where not all elements of a given dimensionality are extended.
- A sub-symmetric stellation is one where not all elements are extended symmetrically.
The Archimedean solids and their duals can also be stellated. Here we usually add the rule that all of the original face planes must be present in the stellation, i.e. we do not consider partial stellations. For example the cube is not usually considered a stellation of the cuboctahedron.
Generalising Miller's rules there are:
- 4 stellations of the rhombic dodecahedron
- 187 stellations of the triakis tetrahedron
- 358,833,097 stellations of the rhombic triacontahedron
- 17 stellations of the cuboctahedron (4 are shown in Wenninger's Polyhedron Models)
- An unknown number of stellations of the icosidodecahedron; there are 7,071,671 non-chiral stellations, but the number of chiral stellations is unknown. (20 are shown in Wenninger's Polyhedron Models)
Seventeen of the nonconvex uniform polyhedra are stellations of Archimedean solids.
Miller's rules
In the book The Fifty-Nine Icosahedra, J.C.P. Miller proposed a set of rules for defining which stellation forms should be considered "properly significant and distinct".
These rules have been adapted for use with stellations of many other polyhedra. Under Miller's rules we find:
- There are no stellations of the tetrahedron, because all faces are adjacent
- There are no stellations of the cube, because non-adjacent faces are parallel and thus cannot be extended to meet in new edges
- There is 1 stellation of the octahedron, the stella octangula
- There are 3 stellations of the dodecahedron: the small stellated dodecahedron, the great dodecahedron and the great stellated dodecahedron, all of which are Kepler–Poinsot polyhedra.
- There are 58 stellations of the icosahedron, including the great icosahedron (one of the Kepler–Poinsot polyhedra), and the second and final stellations of the icosahedron. The 59th model in The fifty nine icosahedra is the original icosahedron itself.
Many "Miller stellations" cannot be obtained directly by using Kepler's method. For example many have hollow centres where the original faces and edges of the core polyhedron are entirely missing: there is nothing left to be stellated. On the other hand, Kepler's method also yields stellations which are forbidden by Miller's rules since their cells are edge- or vertex-connected, even though their faces are single polygons. This discrepancy received no real attention until Inchbald (2002).
Other rules for stellation
Miller's rules by no means represent the "correct" way to enumerate stellations. They are based on combining parts within the stellation diagram in certain ways, and don't take into account the topology of the resulting faces. As such there are some quite reasonable stellations of the icosahedron that are not part of their list – one was identified by James Bridge in 1974, while some "Miller stellations" are questionable as to whether they should be regarded as stellations at all – one of the icosahedral set comprises several quite disconnected cells floating symmetrically in space.
As yet an alternative set of rules that takes this into account has not been fully developed. Most progress has been made based on the notion that stellation is the reciprocal or dual process to facetting, whereby parts are removed from a polyhedron without creating any new vertices. For every stellation of some polyhedron, there is a dual facetting of the dual polyhedron, and vice versa. By studying facettings of the dual, we gain insights into the stellations of the original. Bridge found his new stellation of the icosahedron by studying the facettings of its dual, the dodecahedron.
Some polyhedronists take the view that stellation is a two-way process, such that any two polyhedra sharing the same face planes are stellations of each other. This is understandable if one is devising a general algorithm suitable for use in a computer program, but is otherwise not particularly helpful.
Many examples of stellations can be found in the list of Wenninger's stellation models.
Stellating polytopes
The stellation process can be applied to higher dimensional polytopes as well. A stellation diagram of an n-polytope exists in an (n − 1)-dimensional hyperplane of a given facet.
For example, in 4-space, the great grand stellated 120-cell is the final stellation of the regular 4-polytope 120-cell.
Naming stellations
The first systematic naming of stellated polyhedra was Cayley's naming of the regular star polyhedra (nowadays known as the Kepler–Poinsot polyhedra). This system was widely, but not always systematically, adopted for other polyhedra and higher polytopes.
John Conway devised a terminology for stellated polygons, polyhedra and polychora (Coxeter 1974). In this system the process of extending edges to create a new figure is called stellation, that of extending faces is called greatening and that of extending cells is called aggrandizement (this last does not apply to polyhedra). This allows a systematic use of words such as 'stellated', 'great', and 'grand' in devising names for the resulting figures. For example Conway proposed some minor variations to the names of the Kepler–Poinsot polyhedra.
Stellation to infinity
Wenninger noticed that some polyhedra, such as the cube, do not have any finite stellations. However stellation cells can be constructed as prisms which extend to infinity. The figure comprising these prisms may be called a stellation to infinity. By most definitions of a polyhedron, however, these stellations are not strictly polyhedra.
Wenninger's figures occurred as duals of the uniform hemipolyhedra, where the faces that pass through the center are sent to vertices "at infinity".
From mathematics to art

Alongside from his contributions to mathematics, Magnus Wenninger is described in the context of the relationship of mathematics and art as making "especially beautiful" models of complex stellated polyhedra.[1]

The Italian Renaissance artist Paolo Uccello created a floor mosaic showing a small stellated dodecahedron in the Basilica of St Mark, Venice, c. 1430. Uccello's depiction was used as the symbol for the Venice Biennale in 1986 on the topic of "Art and Science".[2] The same stellation is central to two lithographs by M. C. Escher: Contrast (Order and Chaos), 1950, and Gravitation, 1952.[3]
See also
- The Fifty-Nine Icosahedra
- List of Wenninger polyhedron models includes 44 stellated forms of the octahedron, dodecahedron, icosahedron, and icosidodecahedron, enumerated in the book Polyhedron Models (1974) by Magnus Wenninger
- Polyhedral compound Includes 5 regular compounds and 4 dual regular compounds.
- List of polyhedral stellations
References
- ^ Malkevitch, Joseph. "Mathematics and Art. 5. Polyhedra, tilings, and dissections". American Mathematical Society. Retrieved 1 September 2015.
- ^ Emmer, Michele (2 December 2003). Mathematics and Culture I. Springer Science & Business Media. p. 269. ISBN 978-3-540-01770-7.
- ^ Locher, J. L. (2000). The Magic of M. C. Escher. Harry N. Abrams, Inc. ISBN 0-810-96720-0.
- Bridge, N. J.; Facetting the dodecahedron, Acta Crystallographica A30 (1974), pp. 548–552.
- Coxeter, H.S.M.; Regular complex polytopes (1974).
- Coxeter, H.S.M.; Du Val, P.; Flather, H. T.; and Petrie, J. F. The Fifty-Nine Icosahedra, 3rd Edition. Stradbroke, England: Tarquin Publications (1999).
- Inchbald, G.; In search of the lost icosahedra, The Mathematical Gazette 86 (2002), pp. 208-215.
- Messer, P.; Stellations of the rhombic triacontahedron and beyond, Symmetry: culture and science, 11 (2000), pp. 201–230.
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 0-521-24524-9.
External links
- Weisstein, Eric W. "Stellation". MathWorld.
- Stellating the Icosahedron and Facetting the Dodecahedron
- Stella: Polyhedron Navigator – Software for exploring polyhedra and printing nets for their physical construction. Includes uniform polyhedra, stellations, compounds, Johnson solids, etc.
- Enumeration of stellations
- Vladimir Bulatov Polyhedra Stellation.
- Vladimir Bulatov's Polyhedra Stellations Applet packaged as an OS X application Archived 2016-03-04 at the Wayback Machine
- Stellation Applet
- An Interactive Creation of Polyhedra Stellations with Various Symmetries
- The Fifty-Nine Icosahedra – Applet Archived 2019-12-28 at the Wayback Machine
- 59 Stellations of the Icosahedron, George Hart
- Stellation: Beautiful Math
- Further Stellations of the Uniform Polyhedra, John Lawrence Hudson The Mathematical Intelligencer, Volume 31, Number 4, 2009
