Langbahn Team – Weltmeisterschaft

Spaghettification

For the computer programming term, see Spaghetti code.

Astronaut falling into a black hole (schematic illustration of the spaghettification effect)
Tidal forces acting on a spherical body in a non-homogeneous gravitational field. In this diagram, the gravitational force originates from a source to the right. It shows both the tidal field (thick red arrows) and the gravity field (thin blue arrows) exerted on the body's surface and center (label O) by a source (label S).

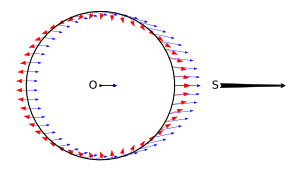
In astrophysics, spaghettification (sometimes referred to as the noodle effect)[1] is the vertical stretching and horizontal compression of objects into long thin shapes (rather like spaghetti) in a very strong, non-homogeneous gravitational field. It is caused by extreme tidal forces. In the most extreme cases, near a black hole, the stretching and compression are so powerful that no object can resist it. Within a small region, the horizontal compression balances the vertical stretching so that a small object being spaghettified experiences no net change in volume.

Stephen Hawking described the flight of a fictional astronaut who, passing within a black hole's event horizon, is "stretched like spaghetti" by the gravitational gradient (difference in gravitational force) from head to toe.[2] The reason this happens would be that the gravitational force exerted by the singularity would be much stronger at one end of the body than the other. If one were to fall into a black hole feet first, the gravity at their feet would be much stronger than at their head, causing the person to be vertically stretched. Along with that, the right side of the body will be pulled to the left, and the left side of the body will be pulled to the right, horizontally compressing the person.[3] However, the term spaghettification was established well before this.[4]

A simple example

The spaghettification of four objects falling towards a planet

In this example, four separate objects are in the space above a planet, positioned in a diamond formation. The four objects follow the lines of the gravitoelectric field,[5] directed towards the celestial body's centre. In accordance with the inverse-square law, the lowest of the four objects experiences the biggest gravitational acceleration, so that the whole formation becomes stretched into a line.

These four objects are connected parts of a larger object. A rigid body will resist distortion, and internal elastic forces develop as the body distorts to balance the tidal forces, so attaining mechanical equilibrium. If the tidal forces are too large, the body may yield and flow plastically before the tidal forces can be balanced, or fracture, producing either a filament or a vertical line of broken pieces.

Inside or outside the event horizon

Spaghettification of a star by a supermassive black hole[6]

The point at which tidal forces destroy an object or kill a person will depend on the black hole's size. For a supermassive black hole, such as those found at a galaxy's center, this point lies within the event horizon, so an astronaut may cross the event horizon without noticing any squashing and pulling, although it remains only a matter of time, as once inside an event horizon, falling towards the center is inevitable.[7] For small black holes whose Schwarzschild radius is much closer to the singularity, the tidal forces would kill even before the astronaut reaches the event horizon.[8][9]

References

Inline citations
  1. ^ Wheeler, J. Craig (2007). Cosmic catastrophes: exploding stars, black holes, and mapping the universe (2nd ed.). Cambridge ; New York: Cambridge University Press. p. 182. ISBN 978-0-521-85714-7. OCLC 73954922.
  2. ^ Hawking, Stephen (1988). A Brief History of Time. Bantam Dell Publishing Group. p. 256. ISBN 978-0-553-10953-5.
  3. ^ Fraknoi, Andrew; Morrison, David; C. Wolff, SIdney (2016). Astronomy. OpenStax. p. 862. ISBN 9781938168284.
  4. ^ Calder, Nigel (1977). The Key to the Universe: A Report on the New Physics. Viking Press. p. 143. ISBN 978-0-67041270-9. Retrieved July 10, 2022. Published as a companion to the BBC TV documentary The Key to the Universe.
  5. ^ Thorne, Kip S. (1988). "Gravitomagnetism, Jets in Quasars, and the Stanford Gyroscope Experiment" (PDF). In Fairbank, J. D.; Deaver, Jr., B. S.; Everitt, C. F.; Micelson, P. F. (eds.). Near Zero: New Frontiers of Physics. New York: W. H. Freeman and Company. pp. 3, 4 (575, 576). From our electrodynamical experience we can infer immediately that any rotating spherical body (e.g., the sun or the earth) will be surrounded by a radial gravitoelectric (Newtonian) field g and a dipolar gravitomagnetic field H. The gravitoelectric monopole moment is the body's mass M; the gravitomagnetic dipole moment is its spin angular momentum S.
  6. ^ Price, Daniel J.; Liptai, David; Mandel, Ilya; Shepherd, Joanna; Lodato, Giuseppe; Levin, Yuri (2024). "Eddington Envelopes: The Fate of Stars on Parabolic Orbits Tidally Disrupted by Supermassive Black Holes". The Astrophysical Journal Letters. 971 (2): L46. arXiv:2404.09381. Bibcode:2024ApJ...971L..46P. doi:10.3847/2041-8213/ad6862.
  7. ^ Hawley, John Frederick; Holcomb, Katherine A. (2005). Foundations of modern cosmology (2nd ed.). Oxford ; New York: Oxford University Press. p. 253. ISBN 978-0-19-853096-1.
  8. ^ Hobson, Michael Paul; Efstathiou, Georges; Lasenby, Anthony N. (2006). General relativity: an introduction for physicists. Cambridge: Cambridge University Press. p. 265. ISBN 978-0-521-82951-9.
  9. ^ Kutner, Marc L. (2003). Astronomy: a physical perspective (2nd ed.). Cambridge: Cambridge University Press. p. 150. ISBN 978-0-521-52927-3.
General references
Quelle: https://en.wikipedia.org/wiki/Spaghettification