Rectangular mask short-time Fourier transform

In mathematics and Fourier analysis, a rectangular mask short-time Fourier transform (rec-STFT) has the simple form of short-time Fourier transform. Other types of the STFT may require more computation time than the rec-STFT.

The rectangular mask function can be defined for some bound (B) over time (t) as

w(t)={\begin{cases}\ 1;&|t|\leq B\\\ 0;&|t|>B\end{cases}}

We can change B for different tradeoffs between desired time resolution and frequency resolution.

Rec-STFT

X(t,f)=\int _{t-B}^{t+B}x(\tau )e^{-j2\pi f\tau }\,d\tau

Inverse form

x(t)=\int _{-\infty }^{\infty }X(t_{1},f)e^{j2\pi ft}\,df{\text{ where }}t-B<t_{1}<t+B

Property

Rec-STFT has similar properties with Fourier transform

Integration

(a)

\int _{-\infty }^{\infty }X(t,f)\,df=\int _{t-B}^{t+B}x(\tau )\int _{-\infty }^{\infty }e^{-j2\pi f\tau }\,df\,d\tau =\int _{t-B}^{t+B}x(\tau )\delta (\tau )\,d\tau ={\begin{cases}\ x(0);&|t|<B\\\ 0;&{\text{otherwise}}\end{cases}}

(b)

\int _{-\infty }^{\infty }X(t,f)e^{-j2\pi fv}\,df={\begin{cases}\ x(v);&v-B<t<v+B\\\ 0;&{\text{otherwise}}\end{cases}}

Shifting property (shift along x-axis)

\int _{t-B}^{t+B}x(\tau +\tau _{0})e^{-j2\pi f\tau }\,d\tau =X(t+\tau _{0},f)e^{j2\pi f\tau _{0}}

Modulation property (shift along y-axis)

\int _{t-B}^{t+B}[x(\tau )e^{j2\pi f_{0}\tau }]d\tau =X(t,f-f_{0})

special input

When $x(t)=\delta (t),X(t,f)={\begin{cases}\ 1;&|t|<B\\\ 0;&{\text{otherwise}}\end{cases}}$
When $x(t)=1,X(t,f)=2B\operatorname {sinc} (2Bf)e^{j2\pi ft}$

Linearity property

If $h(t)=\alpha x(t)+\beta y(t)\,$ , $H(t,f),X(t,f),$ and $Y(t,f)\,$ are their rec-STFTs, then

H(t,f)=\alpha X(t,f)+\beta Y(t,f).

Power integration property

\int _{-\infty }^{\infty }|X(t,f)|^{2}\,df=\int _{t-B}^{t+B}|x(\tau )|^{2}\,d\tau

\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|X(t,f)|^{2}\,df\,dt=2B\int _{-\infty }^{\infty }|x(\tau )|^{2}\,d\tau

Energy sum property (Parseval's theorem)

\int _{-\infty }^{\infty }X(t,f)Y^{*}(t,f)\,df=\int _{t-B}^{t+B}x(\tau )y^{*}(\tau )\,d\tau

\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }X(t,f)Y^{*}(t,f)\,df\,dt=2B\int _{-\infty }^{\infty }x(\tau )y^{*}(\tau )\,d\tau

Example of tradeoff with different B

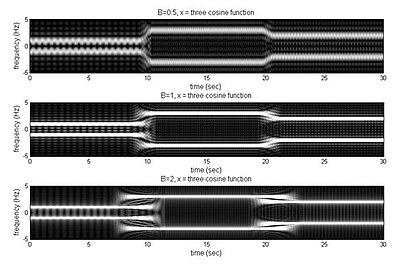
Spectrograms produced from applying a rec-STFT on a function consisting of 3 consecutive cosine waves. (top spectrogram uses smaller B of 0.5, middle uses B of 1, and bottom uses larger B of 2.)

From the image, when B is smaller, the time resolution is better. Otherwise, when B is larger, the frequency resolution is better.

Advantage and disadvantage

Compared with the Fourier transform:

Advantage: The instantaneous frequency can be observed.
Disadvantage: Higher complexity of computation.

Compared with other types of time-frequency analysis:

Advantage: Least computation time for digital implementation.
Disadvantage: Quality is worse than other types of time-frequency analysis. The jump discontinuity of the edges of the rectangular mask results in Gibbs ringing artifacts in the frequency domain, which can be alleviated with smoother windows.

References

Jian-Jiun Ding (2014) Time-frequency analysis and wavelet transform

Fahrer / Team für die Suche eingeben: