Langbahn Team – Weltmeisterschaft

Order-7 heptagonal tiling

Order-7 heptagonal tiling
Order-7 heptagonal tiling
Poincaré disk model of the hyperbolic plane
Type Hyperbolic regular tiling
Vertex configuration 77
Schläfli symbol {7,7}
Wythoff symbol 7 | 7 2
Coxeter diagram
Symmetry group [7,7], (*772)
Dual self dual
Properties Vertex-transitive, edge-transitive, face-transitive

In geometry, the order-7 heptagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {7,7}, constructed from seven heptagons around every vertex. As such, it is self-dual.

Uniform heptaheptagonal tilings
Symmetry: [7,7], (*772) [7,7]+, (772)
=
= 		=
= 		=
= 		=
= 		=
= 		=
= 		=
= 		=
=
{7,7} t{7,7}
 r{7,7} 2t{7,7}=t{7,7} 2r{7,7}={7,7} rr{7,7} tr{7,7} sr{7,7}
Uniform duals
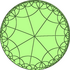
V77 V7.14.14 V7.7.7.7 V7.14.14 V77 V4.7.4.7 V4.14.14 V3.3.7.3.7

This tiling is a part of regular series {n,7}:

Tiles of the form {n,7}
Spherical Hyperbolic tilings

{2,7}
{3,7}
{4,7}
{5,7}
{6,7}
{7,7}
{8,7}
 ...
{∞,7}

See also

References

  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.


Quelle: https://en.wikipedia.org/wiki/Order-7_heptagonal_tiling