g-index
| Part of a series on |
| Citation metrics |
|---|
 |
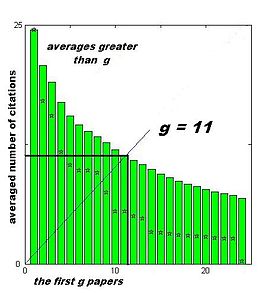
The g-index is an author-level metric suggested in 2006 by Leo Egghe.[1] The index is calculated based on the distribution of citations received by a given researcher's publications, such that given a set of articles ranked in decreasing order of the number of citations that they received, the g-index is the unique largest number such that the top g articles received together at least g2 citations. Hence, a g-index of 10 indicates that the top 10 publications of an author have been cited at least 100 times (102), a g-index of 20 indicates that the top 20 publications of an author have been cited 400 times (202).
It can be equivalently defined as the largest number n of highly cited articles for which the average number of citations is at least n. This is in fact a rewriting of the definition
as
The g-index is an alternative for the older h-index. The h-index does not average the number of citations. Instead, the h-index only requires a minimum of n citations for the least-cited article in the set and thus ignores the citation count of very highly cited publications. Roughly, the effect is that h is the number of works of a quality threshold that rises as h rises; g allows citations from higher-cited works to be used to bolster lower-cited works in meeting this threshold. In effect, the g-index is the maximum reachable value of the h-index if a fixed number of citations can be distributed freely over a fixed number of publications. Therefore, in all cases g is at least h, and is in most cases higher.[1] The g-index often separates authors based on citations to a greater extent compared to the h-index. However, unlike the h-index, the g-index saturates whenever the average number of citations for all publications exceeds the total number of publications; the way it is defined, the g-index is not adapted to this situation. However, if an author with a saturated g-index publishes more, their g-index will increase.
| Author 1 | Author 2 | |
|---|---|---|
| Work 1 | 30 | 10 |
| Work 2 | 17 | 9 |
| Work 3 | 15 | 9 |
| Work 4 | 13 | 9 |
| Work 5 | 8 | 8 |
| Work 6 | 6 | 6 |
| Work 7 | 5 | 5 |
| Work 8 | 4 | 4 |
| Work 9 | 3 | 2 |
| Work 10 | 1 | 1 |
| Total cites | 102 | 63 |
| Average cites | 10,2 | 6,3 |
The g-index has been characterized in terms of three natural axioms by Woeginger (2008).[2] The simplest of these three axioms states that by moving citations from weaker articles to stronger articles, one's research index should not decrease. Like the h-index, the g-index is a natural number and thus lacks in discriminatory power. Therefore, Tol (2008) proposed a rational generalisation.[3][clarification needed]
Tol also proposed a collective g-index.
- Given a set of researchers ranked in decreasing order of their g-index, the g1-index is the (unique) largest number such that the top g1 researchers have on average at least a g-index of g1.
References
- ^ a b Egghe, Leo (2006). "Theory and practise of the g-index". Scientometrics. 69 (1): 131–152. doi:10.1007/s11192-006-0144-7. hdl:1942/981. S2CID 207236267.
- ^ Woeginger, Gerhard J. (2008). "An axiomatic analysis of Egghe's g-index". Journal of Informetrics. 2 (4): 364–368. doi:10.1016/j.joi.2008.05.002.
- ^ Tol, Richard S. J. (2008). "A rational, successive g-index applied to economics departments in Ireland". Journal of Informetrics. 2 (2): 149–155. doi:10.1016/j.joi.2008.01.001. Preprint.


