Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as 2⁻³·3¹·5¹ = 15/8.

Powers of 2 represent intervallic movements by octaves. Powers of 3 represent movements by intervals of perfect fifths (plus one octave, which can be removed by multiplying by 1/2, i.e., 2⁻¹). Powers of 5 represent intervals of major thirds (plus two octaves, removable by multiplying by 1/4, i.e., 2⁻²). Thus, 5-limit tunings are constructed entirely from stacking of three basic purely-tuned intervals (octaves, thirds and fifths). Since the perception of consonance seems related to low numbers in the harmonic series, and 5-limit tuning relies on the three lowest primes, 5-limit tuning should be capable of producing very consonant harmonies. Hence, 5-limit tuning is considered a method for obtaining just intonation.

The number of potential intervals, pitch classes, pitches, key centers, chords, and modulations available to 5-limit tunings is unlimited, because no (nonzero integer) power of any prime equals any power of any other prime, so the available intervals can be imagined to extend indefinitely in a 3-dimensional lattice (one dimension, or one direction, for each prime). If octaves are ignored, it can be seen as a 2-dimensional lattice of pitch classes (note names) extending indefinitely in two directions.

However, most tuning systems designed for acoustic instruments restrict the total number of pitches for practical reasons. It is also typical (but not always done) to have the same number of pitches in each octave, representing octave transpositions of a fixed set of pitch classes. In that case, the tuning system can also be thought of as an octave-repeating scale of a certain number of pitches per octave.

The frequency of any pitch in a particular 5-limit tuning system can be obtained by multiplying the frequency of a fixed reference pitch chosen for the tuning system (such as A440, A442, A432, C256, etc.) by some combination of the powers of 3 and 5 to determine the pitch class and some power of 2 to determine the octave.

For example, if we have a 5-limit tuning system where the base note is C256 (meaning it has 256 cycles per second and we decide to call it C), then f_C = 256 Hz, or "frequency of C equals 256 Hz." There are several ways to define E above this C. Using thirds, one may go up one factor 5 and down two factors 2, reaching a frequency ratio of 5/4, or using fifths one may go up four factors of 3 and down six factors of 2, reaching 81/64. The frequencies become:

or

Assuming we restrict ourselves to seven pitch classes (seven notes per octave), it is possible to tune the familiar diatonic scale using 5-limit tuning in a number of ways, all of which make most of the triads ideally tuned and as consonant and stable as possible, but leave some triads in less-stable intervalic configurations.

The prominent notes of a given scale are tuned so that their frequencies form ratios of relatively small integers. For example, in the key of G major, the ratio of the frequencies of the notes G to D (a perfect fifth) is 3/2, while that of G to C is 2/3 (a descending perfect fifth) or 4/3 (a perfect fourth) going up, and the major third G to B is 5/4.

A just diatonic scale may be derived as follows. Imagining the key of C major, suppose we insist that the subdominant root F and dominant root G be a fifth (3:2) away from the tonic root C on either side, and that the chords FAC, CEG, and GBD be just major triads (with frequency ratios 4:5:6):

Tone	Name	C		D		E		F		G		A		B		C
	Ratio	1/1		9/8		5/4		4/3		3/2		5/3		15/8		2/1
	Natural	24		27		30		32		36		40		45		48
	Cents	0		204		386		498		702		884		1088		1200
Step	Interval		T		t		s		T		t		T		s
	Ratio		9/8		10/9		16/15		9/8		10/9		9/8		16/15
	Cents step		204		182		112		204		182		204		112

This is known as Ptolemy's intense diatonic scale. Here the row headed "Natural" expresses all these ratios using a common list of natural numbers (by multiplying the row above by the lcm of its denominators). In other words, the lowest occurrence of this one-octave scale shape within the harmonic series is as a subset of 7 of the 24 harmonics found in the octave from harmonics 24 to 48.

The three major thirds are correct (5:4), and three of the minor thirds are as expected (6:5), but D to F is a semiditone or Pythagorean minor third (equal to three descending just perfect fifths, octave adjusted), a syntonic comma narrower than a justly tuned (6:5) minor third.

As a consequence, we obtain a scale in which EGB and ACE are just minor triads (10:12:15), but the DFA triad doesn't have the minor shape or sound we might expect, being (27:32:40). Furthermore, the BDF triad is not the (25:30:36) diminished triad that we would get by stacking two 6:5 minor thirds, being (45:54:64) instead:^[1][2]

It can be seen that basic step-wise scale intervals appear:

• s = 16:15 (semitone)
• t = 10:9 (minor tone)
• T = 9:8 (major tone)

which may be combined to form larger intervals (among others):

• Ts = 6:5 (minor third)
• Tt = 5:4 (major third)
• Tts = 4:3 (perfect fourth)
• TTts = 3:2 (perfect fifth)
• TTTttss 2:1 (octave)

Another way to do it is as follows. Thinking in the relative minor key of A minor and using D, A, and E as our spine of fifths, we can insist that the chords DFA, ACE, and EGB be just minor triads (10:12:15):

Tone	Name	A		B		C		D		E		F		G		A
	Ratio	1/1		9/8		6/5		4/3		3/2		8/5		9/5		2/1
	Natural	120		135		144		160		180		192		216		240
	Cents	0		204		316		498		702		814		1018		1200
Step	Interval		T		s		t		T		s		T		t
	Ratio		9/8		16/15		10/9		9/8		16/15		9/8		10/9
	Cents step		204		112		182		204		112		204		182

If we contrast that against the earlier scale, we see that for five pairs of successive notes the ratios of the steps remain the same, but one note, D, the steps C-D and D-E have switched their ratios.

The three major thirds are still 5:4, and three of the minor thirds are still 6:5 with the fourth being 32:27, except that now it's BD instead of DF that is 32:27. FAC and CEG still form just major triads (4:5:6), but GBD is now (108:135:160), and BDF is now (135:160:192).

There are other possibilities such as raising A instead of lowering D, but each adjustment breaks something else.

It is evidently not possible to get all seven diatonic triads in the configuration (4:5:6) for major, (10:12:15) for minor, and (25:30:36) for diminished at the same time if we limit ourselves to seven pitches.

That demonstrates the need for increasing the numbers of pitches to execute the desired harmonies in tune.

To build a twelve-tone scale in 5-limit tuning, we start by constructing a table containing fifteen justly intonated pitches:

Factor	1⁄9	1⁄3	1	3⁄1	9⁄1
5⁄1	D− 10/9 182[3]	A 5/3 884	E 5/4 386	B 15/8 1088	F♯+ 45/32 590[3]	note ratio cents
1	B♭− 16/9 996[3]	F 4/3 498	C 1 0	G 3/2 702	D 9/8 204	note ratio cents
1⁄5	G♭− 64/45 610[3]	D♭− 16/15 112[3]	A♭ 8/5 814	E♭ 6/5 316	B♭ 9/5 1018	note ratio cents

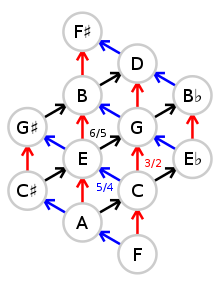
The factors listed in the first row and first column are powers of 3 and 5 respectively (e.g., 1⁄9 = 3⁻²). Colors indicate couples of enharmonic notes with almost identical pitch. The ratios are all expressed relative to C in the centre of this diagram (the base note for this scale). They are computed in two steps:

1. For each cell of the table, a base ratio is obtained by multiplying the corresponding factors. For instance, the base ratio for the lower-left cell is 1/9 · 1/5 = 1/45.
2. The base ratio is then multiplied by a negative or positive power of 2, as large as needed to bring it within the range of the octave starting from C (from 1/1 to 2/1). For instance, the base ratio for the lower left cell (1/45) is multiplied by 2⁶, and the resulting ratio is 64/45, which is a number between 1/1 and 2/1.

Note that the powers of 2 used in the second step may be interpreted as ascending or descending octaves. For instance, multiplying the frequency of a note by 2⁶ means increasing it by 6 octaves. Moreover, each row of the table may be considered a sequence of fifths (ascending to the right), and each column a sequence of major thirds (ascending upward). For instance, in the first row of the table, there is an ascending fifth from D and A, and another one (followed by a descending octave) from A to E. This suggests an alternative but equivalent method for computing the same ratios. For instance, you can obtain A (5/3 ratio), starting from C, by moving one cell to the left and one upward in the table, which means descending by one fifth (2/3) and ascending by one major third (5/4):

Since this is below C, you need to move up by an octave to end up within the desired range of ratios (from 1/1 to 2/1):

A 12-tone scale is obtained by removing one note for each couple of enharmonic notes. This can be done in at least three ways, which have in common the removal of G♭, according to a convention valid even for C-based Pythagorean and 1/4-comma meantone scales. Note that it is a diminished fifth, close to half an octave, above the tonic C, which is a disharmonic interval; also its ratio has the largest values in its numerator and denominator of all tones in the scale, which make it least harmonious: all reasons to avoid it.
The first strategy, which we operationally denote here as symmetric scale 1, consists of selecting for removal the tones in the upper left and lower right corners of the table. The second one, denoted as symmetric scale 2, consists of discarding the notes in the first and last cell of the second row (labeled "1"). The third one, denoted as asymmetric scale, consists of discarding the first column (labeled "1/9"). The resulting 12-tone scales are shown below:

Symmetric scale 1
Factor	1⁄9	1⁄3	1	3	9
5		A 5/3	E 5/4	B 15/8	F♯+ 45/32
1	B♭− 16/9	F 4/3	C 1	G 3/2	D 9/8
1⁄5		D♭− 16/15	A♭ 8/5	E♭ 6/5

Symmetric scale 2
Factor	1⁄9	1⁄3	1	3	9
5	D− 10/9	A 5/3	E 5/4	B 15/8	F♯+ 45/32
1		F 4/3	C 1	G 3/2
1⁄5		D♭− 16/15	A♭ 8/5	E♭ 6/5	B♭ 9/5

Asymmetric scale
Factor	1⁄9	1⁄3	1	3	9
5		A 5/3	E 5/4	B 15/8	F♯+ 45/32
1		F 4/3	C 1	G 3/2	D 9/8
1⁄5		D♭− 16/15	A♭ 8/5	E♭ 6/5	B♭ 9/5

In the first and second scale, B♭ and D are exactly the inversion of each other. This is not true for the third one. This is the reason why these two scales are regarded as symmetric (although the removal of G♭ makes all 12 tone scales, including those produced with any other tuning system, slightly asymmetric).

The asymmetric system has the advantage of having the "justest" ratios (those containing smaller numbers), nine pure fifths (factor 3/2), eight pure major thirds (factor 5/4) by design, but also six pure minor thirds (factor 6/5). However, it also contains two impure fifths (e.g., D to A is 40/27 rather than 3/2) and three impure minor thirds (e.g., D to F is 32/27 rather than 6/5), which practically limits modulation to a narrow range of keys. The chords of the tonic C, dominant G and subdominant F are pure, as well as D♭, A♭, E♭ and the minor chords Fm, Cm, Gm, Am, Bm and Em, but not the Dm.

A drawback of the asymmetric system is that it produces 14 wolf intervals, rather than 12 as for the symmetric ones.

The B♭ in the first symmetric scale differs from the B♭ in the other scales by the syntonic comma, being over 21 cents. In equally tempered scales, the difference is eliminated by making all steps the same frequency ratio.

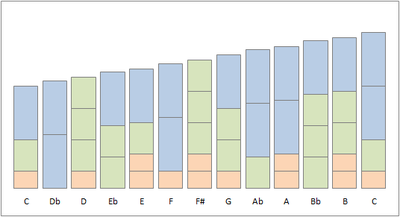The construction of the asymmetric scale is graphically shown in the picture. Each block has the height in cents of the constructive frequency ratios 2/1, 3/2 and 5/4. Recurring patterns can be recognised. For example, many times the next note is created by replacing a 5/4-block and a 3/2-block by a 2/1-block, representing a ratio of 16/15.

For a similar image, built using frequency factors 2, 3, and 5, rather than 2/1, 3/2, and 5/4, see here.

The just ratios used to build these scales can be used as a reference to evaluate the consonance of intervals in other scales (for instance, see this comparison table). However, 5-limit tuning is not the only method to obtain just intonation. It is possible to construct just intervals with even "juster" ratios, or alternately, with values closer to the equal-tempered equivalents. For instance, a 7-limit tuning is sometimes used to obtain a slightly juster and consequently more consonant interval for the minor seventh (7/4) and its inversion, the major second (8/7). A list of these reference ratios, which may be referred to as pure or strictly just intervals or ratios, is provided below:

Interval name	Short	Number of semitones	5-limit tuning				7-limit tuning	17-limit tuning
			Symmetric scales		Asymmetric scales
			N. 1	N. 2	Standard	Extended
Perfect unison	P1	0	1/1	1/1	1/1	1/1	1/1	1/1
Minor second	m2	1	16/15	16/15	16/15	16/15	15/14	14/13
Major second	M2	2	9/8	10/9	9/8	9/8	8/7	8/7
Minor third	m3	3	6/5	6/5	6/5	6/5	6/5	6/5
Major third	M3	4	5/4	5/4	5/4	5/4	5/4	5/4
Perfect fourth	P4	5	4/3	4/3	4/3	4/3	4/3	4/3
Augmented fourth	A4	6	45/32	45/32	45/32	25/18	7/5	7/5 or 17/12
Diminished fifth	d5	6	64/45	64/45	64/45	36/25	10/7	10/7 or 24/17
Perfect fifth	P5	7	3/2	3/2	3/2	3/2	3/2	3/2
Minor sixth	m6	8	8/5	8/5	8/5	8/5	8/5	8/5
Major sixth	M6	9	5/3	5/3	5/3	5/3	5/3	5/3
Minor seventh	m7	10	16/9	9/5	9/5	9/5	7/4	7/4
Major seventh	M7	11	15/8	15/8	15/8	15/8	15/8	13/7
Perfect octave	P8	12	2/1	2/1	2/1	2/1	2/1	2/1

Cells highlighted in yellow indicate intervals that are juster than those in the non-coloured cells in the same row. Those highlighted in cyan indicate even juster ratios.

Notice that the ratios 45/32 and 64/45 for the tritones (augmented fourth and diminished fifth) are not in all contexts regarded as strictly just, but they are the justest possible in the above-mentioned 5-limit tuning scales. An extended asymmetric 5-limit scale (see below) provides slightly juster ratios for both the tritones (25/18 and 36/25), the purity of which is also controversial. 7-limit tuning allows for the justest possible ratios, namely 7/5 (about 582.512 cents, also known as septimal tritone) and 10/7 (about 617.488 cents). These ratios are more consonant than 17/12 (about 603.000 cents) and 24/17 (about 597.000 cents), which can be obtained in 17-limit tuning, yet the latter are also fairly common, as they are closer to the equal-tempered value of 600.000 cents.

The above-mentioned 7/4 interval (about 968.826 cents), also known as the septimal minor seventh, or harmonic seventh, has been a contentious issue throughout the history of music theory; it is 31 cents flatter than an equal-tempered minor seventh.

The tables above only show the frequency ratios of each note with respect to the base note. However, intervals can start from any note and so twelve intervals can be defined for each interval type – twelve unisons, twelve semitones, twelve 2-semitone intervals, etc.

In 5-limit tuning, each interval type except for unisons and octaves has three or four different sizes. This is the price paid for seeking just intonation. The table on the right shows their frequency ratios for the asymmetric scale, with deviations coloured and deviations corresponding to wolf intervals in purple. The deviations arise because the notes determine four different semitones:

("Just" augmented unison between E♭ and E)

(Augmented unison between D♭ and D)

("Just" minor second between C and D♭)

(Minor second between A and B♭)

By contrast, in an equally tempered chromatic scale, all semitones measure

and intervals of any given type have the same size, but none are justly tuned except unisons and octaves.

In other tuning systems, a comma may be defined as a minute interval, equal to the difference between two kinds of semitones (diatonic and chromatic, also known as minor second, m2, or augmented unison, A1). In this case, however, 4 kinds of semitones are produced (two A1, S₁ and S₂, and two m2, S₃ and S₄) and 12 different commas can be defined as the differences between their sizes in cents, or equivalently as the ratios between their ratios. Among these, we select the six ascending ones (those with ratio larger than 1/1, and positive size in cents):

Name of comma	Equivalent definitions		Size
	In meantone temperament	In 5-limit tuning (asymmetric scale)	Ratio	Cents
Diaschisma (DS)	in 1/6-comma meantone
Syntonic comma (SC)
Lesser diesis (LD)	in 1/4-comma meantone
Greater diesis (GD)	in 1/3-comma meantone

The other six ratios are discarded because they are just the opposite of these, and hence they have exactly the same length, but an opposite direction (i.e., a descending direction, a ratio smaller than 1/1, and a negative size in cents). We obtain commas of four different sizes: the diaschisma, the lesser diesis, the syntonic comma, and the greater diesis. Since S₁ (the just A1) and S₃ (the just m2) are the most often occurring semitones in this 12-tone scale (see tables above), the lesser diesis, being defined as the ratio between them, is the most often observed comma.

The syntonic comma is also defined, in 5-limit tuning, as the ratio between the major tone (M2 with size 9/8) and the minor tone (M2 with size 10/9). Notice that it cannot be defined, in other tuning systems, as the ratio between diatonic and chromatic semitones (m2/A1), but it is an important reference value used to tune the perfect fifth in any tuning system in the syntonic temperament continuum (including also meantone temperaments).

Three of the above-mentioned commas, namely the diaschisma, the diesis and the greater diesis, meet the definition of the diminished second, being the difference between the sizes in cents of a diatonic and a chromatic semitone (or equivalently the ratio between their frequency ratios).

On the contrary, the syntonic comma is defined either as the difference in cents between two chromatic semitones (S₂ and S₁), or between two diatonic semitones (S₄ and S₃), and cannot be considered a diminished second.

The table above uses only low powers of 3 and 5 to build the base ratios. However, it can be easily extended by using higher positive and negative powers of the same numbers, such as 5² = 25, 5⁻² = 1/25, 3³ = 27, or 3⁻³ = 1/27. A scale with 25, 35, or even more pitches can be obtained by combining these base ratios.

For instance, one can obtain 35 pitches by adding rows in each direction like this:

Factor		1/9	1/3	1	3	9
125	note ratio cents	A♯ 125/72 955.0[3]	E♯ 125/96 457.0	B♯ 125/64 1158.9	F+ 375/256 660.9[3]	C+ 1125/1024 162.9[3]
25	note ratio cents	F♯ 25/18 568.7[3]	C♯ 25/24 70.7	G♯ 25/16 772.6	D♯ 75/64 274.6	A♯+ 225/128 976.5[3]
5	note ratio cents	D− 10/9 182.4	A 5/3 884.4	E 5/4 386.3	B 15/8 1088.3	F♯+ 45/32 590.2
1	note ratio cents	B♭− 16/9 996.1	F 4/3 498.0	C 1/1 0.0	G 3/2 702.0	D 9/8 203.9
1/5	note ratio cents	G♭− 64/45 609.8	D♭− 16/15 111.7	A♭ 8/5 813.7	E♭ 6/5 315.6	B♭ 9/5 1017.6
1/25	note ratio cents	E− 256/225 223.5[3]	B− 128/75 925.4[3]	F♭ 32/25 427.4	C♭ 48/25 1129.3	G♭ 36/25 631.3
1/125	note ratio cents	C− 2048/1125 1037.1[3]	G− 512/375 539.1[3]	D− 128/125 41.1[3]	A 192/125 743.0	E 144/125 245.0

The left column (1/9) is sometimes removed (as in the asymmetric scale shown above), thus creating an asymmetric table with a smaller number of pitches. Notice that a juster ratio is produced for the diminished fifth (C-G♭ = 36/25), with respect to the restricted 5-limit tuning described above (where C to G♭- = 64/45).^[4]

In Pythagorean tuning, perhaps the first tuning system theorized in the West,^[5] the only highly consonant intervals were the perfect fifth and its inversion, the perfect fourth. The Pythagorean major third (81:64) and minor third (32:27) were dissonant, and this prevented musicians from using triads and chords, forcing them for centuries to write music with relatively simple texture. In late Middle Ages, musicians realized that by slightly tempering the pitch of some notes, the Pythagorean thirds could be made consonant. For instance, if you decrease by a syntonic comma (81:80) the frequency of E, C-E (a major third), and E-G (a minor third) become just. Namely, C-E is narrowed to a justly intonated ratio of

and at the same time E-G is widened to the just ratio of

The drawback is that the fifths A-E and E-B, by flattening E, become almost as dissonant as the Pythagorean wolf fifth. But the fifth C-G stays consonant, since only E has been flattened (C-E * E-G = 5/4 * 6/5 = 3/2), and can be used together with C-E to produce a C-major triad (C-E-G).

By generalizing this simple rationale, Gioseffo Zarlino, in the late sixteenth century, created the first justly intonated 7-tone (diatonic) scale, which contained pure perfect fifths (3:2), pure major thirds, and pure minor thirds:

F → A → C → E → G → B → D

This is a sequence of just major thirds (M3, ratio 5:4) and just minor thirds (m3, ratio 6:5), starting from F:

F + M3 + m3 + M3 + m3 + M3 + m3

Since M3 + m3 = P5 (perfect fifth), i.e., 5/4 * 6/5 = 3/2, this is exactly equivalent to the diatonic scale obtained in 5-limit just intonation, and hence can be viewed as a subset of the construction table used for the 12-tone (chromatic) scale:

A	→	E	→	B
↑		↑		↑
F	→	C	→	G	→	D

where both rows are sequences of just fifths, and F-A, C-E, G-B are just major thirds:

M3		M3		M3
+		+		+
F	+	P5	+	P5	+	P5

• Mathematics of musical scales
• Microtonal music
• Microtuner
• Pythagorean interval
• Semitone
• List of intervals in 5-limit just intonation
• List of meantone intervals
• List of musical intervals
• List of pitch intervals
• Whole-tone scale
• Regular number
• Hexany
• Electronic tuner
• Consonance and dissonance

• Art of the States: microtonal/just intonation works using just intonation by American composers
• The Chrysalis Foundation – Just Intonation: Two Definitions
• Dante Rosati's 21 Tone Just Intonation guitar
• Just Intonation by Mark Nowitzky
• Just Intonation Explained by Kyle Gann
• A selection of Just Intonation works edited by the Just Intonation Network web published on the Tellus Audio Cassette Magazine project archive at UbuWeb
• Medieval Music and Arts Foundation
• Music Novatory – Just Intonation Archived 2011-06-15 at the Wayback Machine
• Why does Just Intonation sound so good?
• The Wilson Archives
• Barbieri, Patrizio. Enharmonic instruments and music, 1470–1900. (2008) Latina, Il Levante
• 22 Note Just Intonation Keyboard Software with 12 Indian Instrument Sounds Libreria Editrice
• Plainsound Music Edition – Just intonation (JI) music and research, information about the Helmholtz-Ellis JI pitch notation