In the music theory of harmony, the root is a specific note that names and typifies a given chord. Chords are often spoken about in terms of their root, their quality, and their extensions. When a chord is named without reference to quality, it is assumed to be major—for example, a "C chord" refers to a C major triad, containing the notes C, E, and G. In a given harmonic context, the root of a chord need not be in the bass position, as chords may be inverted while retaining the same name, and therefore the same root.

In tertian harmonic theory, wherein chords can be considered stacks of third intervals (e.g. in common practice tonality), the root of a chord is the note on which the subsequent thirds are stacked. For instance, the root of a triad such as E Minor is E, independently of the vertical order in which the three notes (E, G and B) are presented. A triad can be in three possible positions, a "root position" with the root in the bass (i.e., with the root as the lowest note, thus E, G, B or E, B, G from lowest to highest notes), a first inversion, e.g. G, B, E or G, E, B (i.e., with the note which is a third interval above the root, G, as the lowest note) and a second inversion, e.g. B, E, G or B, G, E, in which the note that is a fifth interval above the root (B) is the lowest note.

Regardless of whether a chord is in root position or in an inversion, the root remains the same in all three cases. Four-note seventh chords have four possible positions. That is, the chord can be played with the root as the bass note, the note a third above the root as the bass note (first inversion), the note a fifth above the root as the bass note (second inversion), or the note a seventh above the root as the bass note (third inversion). Five-note ninth chords know five positions, six-note eleventh chords know six positions, etc., but the root position always is that of the stack of thirds, and the root is the lowest note of this stack (see also Factor (chord)).

The idea of chord root links to that of a chord's root position, as opposed to its inversion. When speaking of a "C triad" (C E G), the name of the chord (C) also is its root. When the root is the lowest note in the chord, it is in root position. When the root is a higher note (E G C or G C E), the chord is inverted but retains the same root. Classified chords in tonal music usually can be described as stacks of thirds (even although some notes may be missing, particularly in chords containing more that three or four notes, i.e. 7ths, 9ths, and above). The safest way to recognize a chord's root, in these cases, is to rearrange the possibly inverted chord as a stack of thirds: the root then is the lowest note.

There are shortcuts to this: in inverted triads, the root is directly above the interval of a fourth, in inverted sevenths, it is directly above the interval of a second.^[1] With chord types, such as chords with added sixths or chords over pedal points, more than one possible chordal analysis may be possible. For example, in a tonal piece of music, the notes C, E, G, A, sounded as a chord, could be analyzed as a C major sixth chord in root position (a major triad – C, E, G – with an added sixth – A – above the root) or as a first inversion A minor seventh chord (the A minor seventh chord contains the notes A, C, E and G, but in this example, the C note, the third of the A minor chord, is in the bass). Deciding which note is the root of this chord could be determined by considering context. If the chord spelled C, E, G, A occurs immediately before a D⁷ chord (spelled D, F♯, A, C), most theorists and musicians would consider the first chord a minor seventh chord in first inversion, because the progression ii⁷–V⁷ is a standard chord movement.

Various devices have been imagined to notate inverted chords and their roots:

• Chord names and symbols (e.g., C major, A minor, G⁷ etc.)
• Roman numeral analysis (e.g., I to indicate the tonic chord and V to indicate the dominant chord)
• Slash chords (e.g., G/B bass, which instructs the chord-playing performer to play a G major triad with a "B" in bass voice/lowest note)

The concept of root has been extended for the description of intervals of two notes: the interval can either be analyzed as formed from stacked thirds (with the inner notes missing): third, fifth, seventh, etc., (i.e., intervals corresponding to odd numerals), and its low note considered as the root; or as an inversion of the same: second (inversion of a seventh), fourth (inversion of a fifth), sixth (inversion of a third), etc., (intervals corresponding to even numerals) in which cases the upper note is the root. See Interval.

Some theories of common-practice tonal music admit the sixth as a possible interval above the root and consider in some cases that ⁶
₅ chords nevertheless are in root position – this is the case particularly in Riemannian theory. Chords that cannot be reduced to stacked thirds (e.g. chords of stacked fourths) may not be amenable to the concept of root, although in practice, in a lead sheet, the composer may specify that a quartal chord has a certain root (e.g., a fake book chart that indicates that a song uses an A^{sus4(add♭7)} chord, which would use the notes A, D, G. Even though this is a quartal chord, the composer has indicated that it has a root of A.)

A major scale contains seven unique pitch classes, each of which might serve as the root of a chord:

Chords in atonal music are often of indeterminate root, as are equal-interval chords and mixed-interval chords; such chords are often best characterized by their interval content.^[3]

The first mentions of the relation of inversion between triads appears in Otto Sigfried Harnish's Artis musicae (1608), which describes perfect triads in which the lower note of the fifth is expressed in its own position, and imperfect ones, in which the base (i.e., root) of the chord appears only higher. Johannes Lippius, in his Disputatio musica tertia (1610) and Synopsis musicae novae (1612), is the first to use the term "triad" (trias harmonica); he also uses the term "root" (radix), but in a slightly different meaning.^[4] Thomas Campion, A New Way of Making Fowre Parts in Conterpoint, London, c. 1618, notes that when chords are in first inversions (sixths), the bass is not "a true base", which is implicitly a third lower. Campion's "true base" is the root of the chord.^[5]

Full recognition of the relationship between the triad and its inversions is generally credited to Jean-Philippe Rameau and his Traité d’harmonie (1722). Rameau was not the first to discover triadic inversion,^[6] but his main achievement is to have recognized the importance of the succession of roots (or of chords identified by their roots) for the construction of tonality (see below, Root progressions).

The concept of chord root is not the same as that of the fundamental of a complex vibration. When a harmonic sound, i. e. a sound with harmonic partials, lacks a component at the fundamental frequency itself, the pitch of this fundamental frequency may nevertheless be heard: this is the missing fundamental. The effect is increased by the fact that the missing fundamental also is the difference tone of the harmonic partials.

Chord notes, however, do not necessarily form a harmonic series. In addition, each of these notes has its own fundamental. The only case where the chord notes may seem to form a harmonic series is that of the major triad. However, the major triad may be formed of the intervals of a third and a fifth, while the corresponding harmonic partials are distant by the intervals of a 12th and a 17th. For instance, C3 E3 G3 is a major triad, but the corresponding harmonic partials would be C3, G4 and E5. The root of the triad is an abstract C, while the (missing) fundamental of C3 E3 G3 is C1 – which would usually not be heard.

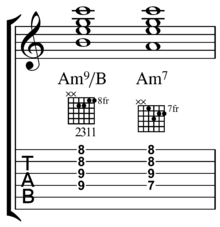
An assumed root (also absent, or omitted root) is "when a chord does not contain a root ([which is] not unusual)".^[8] In any context, it is the unperformed root of a performed chord. This 'assumption' may be established by the interaction of physics and perception, or by pure convention. "We only interpret a chord as having its root omitted when the habits of the ear make it absolutely necessary for us to think of the absent root in such a place."[emphasis original].^[9] "We do not acknowledge omitted Roots except in cases where the mind is necessarily conscious of them ... There are also cases in instrumental accompaniment in which the root having been struck at the commencement of a measure, the ear feels it through the rest of the measure" (emphasis in original).^[10]

In guitar tablature, this may be indicated, "to show you where the root would be", and to assist one with, "align[ing] the chord shape at the appropriate fret", with an assumed root in grey, other notes in white, and a sounded root in black.^[7]

An example of an assumed root is the diminished seventh chord, of which a note a major third below the chord is often assumed to be the absent root, making it a ninth chord.^[13] The diminished seventh chord affords, "singular facilities for modulation", as it may be notated four ways, to represent four different assumed roots.^[12]

In jazz and jazz fusion, roots are often omitted from chords when chord-playing musicians (e.g., electric guitar, piano, Hammond organ) are improvising chords in an ensemble that includes a bass player (either double bass, electric bass, or other bass instruments), because the bass player plays the root. For example, if a band is playing a tune in the key of C major, if there is a dominant seventh chord played on the dominant chord (i.e., G⁷), the chord-playing musicians typically do not play the G note in their voicing of the chord, as they expect the bass player to play the root. The chord playing musicians usually play a voicing that includes the third, seventh, and additional extensions (often the ninth and thirteenth, even if they are not specified in the chord chart). Thus a typical voicing by a chord-playing musician for a G⁷ chord would be the notes B and F (the third and flat seventh of the chord), along with the notes A and E (the ninth and thirteenth of the G⁷ chord). One possible voicing for this G⁷ chord would be the notes B, E, F, A (the third, thirteenth, seventh and ninth of the G⁷ chord). (Note: the thirteenth interval is the same "pitch class" as the sixth, except that it is one octave higher; the ninth is the same "pitch class" as the second interval, except that it is one octave higher.)

The fundamental bass (basse fondamentale) is a concept proposed by Jean-Philippe Rameau, derived from the thoroughbass, to notate what would today be called the progression of chord roots rather than the actual lowest note found in the music, the bassline. From this Rameau formed rules for the progression of chords based on the intervals between their roots. Subsequently, music theory has typically treated chordal roots as the defining feature of harmony.^[14]

Why is it so important to know the root of the chord? Because the roots of the chords will sound whether we want them to or not, whether or not the alphabetical symbol is correct. The root progression which emerges may not coincide with what we think we have written; it may be better or it may be worse; but art does not permit chance. The root progression supports the work. The total root progression is heard as a substantive element, almost like another melody, and it determines the tonal basis of the music. And the tonal basis of a piece is very important to the construction of themes and to the orchestration.^[15]

Roman numeral analysis may be said to derive from the theory of the fundamental bass, although it does not particularly theorize the succession of roots. The theory of the fundamental bass properly speaking has been revived in the 20th century by Arnold Schoenberg,^[16] Yizhak Sadaï^[17] and Nicolas Meeùs.^[18]

• Figured bass