Sexagesimalsystem
Das Sexagesimalsystem (auch Hexagesimalsystem oder Sechziger-System) ist ein Zahlensystem zur Basis 60 (lateinisch sexagesimus ‚der Sechzigste‘). Seine größte Bedeutung bekam es in der Zeit der babylonischen Hochkultur, in der die Astronomie samt der dazu erforderlichen Messtechnik und Mathematik gepflegt wurde.
Die Sechziger-Teilung hat sich in der Art, in der Winkeleinheiten unterteilt werden, bis in die Gegenwart erhalten. Ein Grad hat 60 Winkelminuten und eine Minute hat 60 Sekunden. Auch in der Zeitmessung ist diese Unterteilung noch üblich. Eine Stunde hat 60 Minuten und eine Minute 60 Sekunden. Im Spätmittelalter haben einige Mathematiker für ihre Berechnungen die Sekunden in Tertien weiter unterteilt. Dies hat sich jedoch nicht durchgesetzt.
Herkunft
Erstmalige Nachweise eines schriftlichen sexagesimalen Rechensystems, das jedoch noch ein Additionssystem war, reichen in die Zeit der Sumerer um 3300 v. Chr. zurück. Im weiteren Verlauf wurde in der babylonischen Mathematik ab ca. 2000 v. Chr. ein sexagesimales Stellenwertsystem verwendet. Die Hauptquellen zur Mathematik stammen aus der Zeit 1900 v. Chr. bis 1600 v. Chr., die ältesten Tabellentexte sind jedoch noch aus neusumerischer Zeit. Die nachalexandrinische Zeit zeigt unter den Seleukiden zunehmend griechische Einflüsse, die eine Synergie mit den babylonischen Kenntnissen eingingen, um später die gesammelten Erfahrungen der Sumerer, Akkader, Assyrer und Babylonier vollends nach Griechenland zu exportieren. Arabische Astronomen benutzten in ihren Sternenkarten und -tabellen die Schreibweise des berühmten griechischen Astronomen Ptolemäus (circa 100–170), die auf sexagesimalen Brüchen basierte. Auch frühe europäische Mathematiker wie Fibonacci (1170–1240) benutzten solche Brüche, wenn sie nicht mit ganzen Zahlen operieren konnten.
Ein Motiv für die Einführung eines Sexagesimalsystems sehen viele Historiker in der Astronomie, da die babylonischen Jahre zwölf Monate zu 30 Tagen umfassten, es gab aber auch etwa alle drei Jahre einen zusätzlichen 13. Schaltmonat.[1] Weitere Hinweise finden sich in der frühen Zählung der Mondmonate, die bis in das Jahr 35 000 v. Chr. nachgewiesen werden können (Kalender-Stöckchen). In der Republik Tschechien wurde der Speichenknochen eines jungen Wolfes von etwa 30 000 v. Chr. entdeckt, der eine Reihe von insgesamt 55 Einkerbungen aufweist, wobei die 9., die 30. und die 31. Kerbe von oben rund doppelt so lang sind wie die anderen Kerben.[2] Weil die mittlere Periode der Mondphasen 29,53 Tage beträgt, könnten die Markierungen mit den Mondphasen in Verbindung stehen.
Andere Wissenschaftler sehen als Grund für die Wahl der Zahl 60 als Basis des Rechensystems die Absicht, möglichst viele der beim praktischen Zählen und Messen (Handel) auftretenden Teile einfach ausdrücken bzw. berechnen zu können.[3] Ein Indiz dafür ist, dass die 60 mit 12 Teilern zu den hochzusammengesetzten Zahlen (Nr. 9 in Folge A002182 in OEIS) gehört.
Das Sexagesimalsystem der Sumerer
Die Zahlzeichen
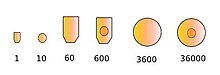
Die Sumerer verwendeten vor den keilschriftlichen Zeichen für die Zahlen 1 und 60 jeweils unterschiedlich große Halbellipsen und für die Zahlen 10 und 3600 = 602 jeweils unterschiedlich große Kreise, die mit zylinderförmigen Griffeln in Tontafeln gedrückt wurden. Aus diesen Zeichen wurden noch die Zeichen für 600 = 10·60 und 36 000 = 10·602 entsprechend kombiniert. Daneben gab es auch noch ein anderes System mit einer dezimalen Stufung 1, 10 und 100, sowie ein drittes System in akkadischer Zeit. Bis zur spätsumerischen Zeit veränderten die einzelnen Zeichen zwar ihre Form, behielten jedoch ihren individuellen Charakter und bildeten ein Additionssystem ähnlich den römischen Zahlen.
Die Zahlennamen
Bei den Sumerern[4] trug die 60 den Namen gesch.
- 120: gesch-min (60 × 2)
- 180: gesch-esch (60 × 3)
- 240: gesch-limmu (60 × 4)
- 300: gesch-iá (60 × 5)
- 360: gesch-asch (60 × 6)
- 420: gesch-imin (60 × 7)
- 480: gesch-ussu (60 × 8)
- 540: gesch-ilummu (60 × 9)
- 600: gesch-u (60 × 10)
- Nun zählten die Sumerer nicht in 60er-Schritten (gesch-Schritten) weiter, sondern in 600er-Schritten (gesch-u-Schritten), und zwar sechsmal 600, also bis 3600, das schàr genannt wurde.
- Die 3600 wurden dann wieder zehnmal gesteigert bis schàr-u (3600 × 10) 36 000.
- Die 36 000 wurden sechsmal gezählt bis 216 000 schàr-gal, wörtlich das große 3600 (also 60 × 60 × 60).
- Die 216 000 wurde zehnmal gezählt bis 2 160 000 schàr-gal-u (=(60 ×60 × 60) × 10)
- Das schàr-gal-u wurde zunächst fünfmal vervielfacht. Die sechste Vielfache 12 960 000, also 60 × 60 × 60 × 60, erhielt wieder einen eigenen Namen, und zwar schàr-gal-shu-nu-tag (dem großen schàr übergeordnete Einheit).
Die Namen der Zahlen 10 bis 60 haben eine dezimale (30 = uschu = esch-u = 3 × 10), und teilweise sogar vigesimale Struktur (40 = nischmin = nisch-min = 20 × 2).[5]
Das Sexagesimalsystem der Babylonier
Struktur
Im späteren babylonischen Sexagesimalsystem hat sich eine Zahlschrift entwickelt, die ein Additionssystem verwendet, dem noch ein Stellenwertsystem mit der Basis 60 überlagert wird. Letzteres ist allerdings noch nicht so weit ausgebildet, dass es heutigen Anforderungen entspricht. Die Zahlenwerte von 1 bis 59 werden unter Verwendung einer Hilfsbasis 10 kumulativ zusammengesetzt aus nur zwei Ziffern[6]
Eigentlich wären für ein Sexagesimalsystem 60 Zahlenwerte nötig, aber ein Leerzeichen und auch eine Null fehlen.
Im babylonischen System können diese 59 Zahlzeichen wie Ziffern im Sinne des heutigen Stellenwertsystems betrachtet und zur Darstellung höherwertiger Zahlen nebeneinander geschrieben werden. Jedes der 59 Zeichen belegt jeweils eine Stelle. Es erhält einen Wert, der sich aus dem Produkt von Zeichenwert und Stellenwert ergibt, so wie das vom Dezimalsystem bekannt ist.[7]
Die Zahlzeichen
Die Zahlzeichen werden in Keilschrift geschrieben. Einige Beispiele sollen das Sexagesimalsystem erklären.

- Zahlzeichen gemäß Additionssystem und entsprechende Schreibweise mit Dezimalziffern:
- Damit zusammengesetzte Zahlzeichen gemäß Stellenwertsystem:
Die Zahlzeichen für die Werte 1 bis 59 setzten sich aus den zwei Keilschrift-Ziffern zusammen in der erforderlichen Anzahl von Wiederholungen. Für das Zeichen einer Sexadezimalzahl ab dem Wert größer als 60 werden zwei oder mehr dieser Zahlzeichen nebeneinander geschrieben. Insofern ist die Anzahl der möglichen Zahlzeichen nicht begrenzt. Ein Problem aus heutiger Sicht ist der Wert 60, bei dem es keinen Wert auf einer „Einerstelle“ gibt; diese Stelle war unbelegt, und dafür konnte nichts geschrieben werden.
Das führt in der Umkehrung auf ein Problem beim Lesen dieser zusammengesetzten Zahlzeichen. Denn der jeweilige Stellenwert eines Zahlzeichens ist nicht eindeutig, wenn sich eine Stelle in heutiger Sicht zu null ergibt, damit in babylonischer Konvention leer bleibt und fehlt. Ob und wo eine Stelle fehlt, kann sich nur aus dem Zusammenhang ergeben.
Später wurde bei einer fehlenden Stelle eine Lücke gelassen, ab dem 6. Jahrhundert v. Chr. kam ein Leerzeichen ohne Wert als weiteres Zeichen auf. Mit diesem Leerzeichen wurde aber nicht gerechnet, und es kam auch nicht als eigenständiges Zahlzeichen vor, es hatte also nicht die Bedeutung einer Ziffer mit dem Wert null. Diese Bedeutung des Leerzeichens ist eine spätere Erfindung indischer Gelehrter.
Will man heutzutage Sexagesimalzahlen wiedergegeben, so werden einzelne Sexagesimal-Zahlzeichen als Dezimalzahlen geschrieben und dazwischen ein Komma gesetzt. Die ganzzahligen Sexagesimalstellen werden von den gebrochenen durch ein Semikolon abgetrennt, und bei fehlenden Stellen bzw. Leerzeichen schreibt man eine „0“ (was dann jedoch Interpretation ist).
- Beispiele: 30,0 = 30·60+0 und 0;30 = 0+30/60.
Die Rechentechnik
Addieren und Subtrahieren
Durch das Stellenwertsystem konnte, wie bei unserem Dezimalsystem, die vorangehende Stelle um jeweils 1 erweitert oder reduziert werden. Durch die Form der Keile war das Sexagesimalsystem leichter, da nur die Keile zusammengesetzt werden mussten. Als Fachausdrücke für die Addition und die Subtraktion wurden „Vermehren“ bzw. „Wegziehen“ verwendet (die mathematischen Symbole + und − führte erst Johannes Widmann im 15. Jahrhundert n. Chr. ein). Eine negative Differenz zweier Zahlen drückte man mit „Subtrahend geht darüber hinaus“ aus. Das Addieren und Subtrahieren funktioniert ebenso wie heute im Dezimalsystem.
Beispiel einer Addition:

 in Schreibweise des Sexagesimalsystems. Die 1 vor dem Komma gibt den Wert 1·60 an, zu dem die Zahl 30 nach dem Komma addiert wird.
in Schreibweise des Sexagesimalsystems. Die 1 vor dem Komma gibt den Wert 1·60 an, zu dem die Zahl 30 nach dem Komma addiert wird.
Beispiel einer Subtraktion:
Multiplizieren
Auch bei der Multiplikation wurde wie im Dezimalsystem verfahren. Während man aber im Dezimalsystem das kleine Einmaleins von 1·1 bis 9·9 im Kopf haben muss, hätten die Babylonier das Einmaleins von 1·1 bis 59·59 auswendig können müssen. Zur Erleichterung wurden Multiplikationstabellen verwendet, von denen man benötigte Produkte ablesen konnte: Jede Zeile einer Multiplikationstabelle begann mit der gleichen Kopfzahl, z. B. 2, es folgte der Ausdruck „mal“ und der Multiplikator, z. B. 1, und schließlich das Ergebnis, z. B. 2. Die Multiplikatoren gingen dabei von 1 bis 20 und danach kamen noch 30, 40 und 50.
Weil im Sexagesimalsystem 60 in 10er Schritten gestuft wurde (siehe oben unter Zahlzeichen) und im allgemeinen, täglichen Leben Dezimalzahlen viel in Gebrauch waren, wurden auch zu Kopfzahlen wie z. B. 1,40 = 100 und 16,40 = 1000 Multiplikationstabellen angelegt. Ein weiterer Grund ist das Zusammenwirken mit den Werten aus Reziprokentabellen (siehe unten unter Division). Wurden andere Werte benötigt, setzte man die Zahlen zusammen.
Die Kopfzahlen:
| 1,15 | 1,20 | 1,30 | 1,40 | 2 | 2,13,20 | 2,15 | 2,24 | 2,30 | 3 | 3,20 | 3,45 | 4 | 4,30 | 5 | 6 | 6,40 | 7 | 7,12 | 7,30 | 8 |
| 8,20 | 9 | 10 | 12 | 12,30 | 15 | 16 | 16,40 | 18 | 20 | 22,30 | 24 | 25 | 30 | 36 | 40 | 44,26,40 | 45 | 48 | 50 |
Beispiel einer Multiplikation:
- .
Dividieren
Die Babylonier dividierten eine Zahl durch eine Zahl , indem sie mit dem Kehrwert von multiplizierten:
- .
Den Kehrwert einer Zahl konnte man in einer Multiplikationstabelle mit der Kopfzahl finden, falls eine Potenz von 60 teilte. Stand dort als Ergebnis ![]() , d. h. eine Potenz von 60, dann war der zugehörige Multiplikator der gesuchte Kehrwert ( und haben im babylonischen Sexagesimalsystem die gleiche Darstellung):
, d. h. eine Potenz von 60, dann war der zugehörige Multiplikator der gesuchte Kehrwert ( und haben im babylonischen Sexagesimalsystem die gleiche Darstellung):
- , also .
Die Kehrwerte (Reziproke) von natürlichen Zahlen stellte man zur Erleichterung wieder in Reziprokentabellen zusammen. Man schrieb in solchen Tabellen bei Werten, die in einer Multiplikationstabelle keinen Kehrwert hatten, „ist nicht“ an Stelle des Kehrwertes. Für diese irregulären Zahlen, die Primfaktoren ≥ 7 besitzen, wurden wie für irrationale Zahlen Näherungswerte verwendet.
Die hauptsächlich verwendete Reziprokentabelle enthält die folgenden Zahlenpaare:
| n | 1/n | n | 1/n | n | 1/n | n | 1/n | n | 1/n | n | 1/n | n | 1/n | n | 1/n | n | 1/n | n | 1/n |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 30 | 3 | 20 | 4 | 15 | 5 | 12 | 6 | 10 | 8 | 7,30 | 9 | 6,40 | 10 | 6 | 12 | 5 | 15 | 4 |
| 16 | 3,45 | 18 | 3,20 | 20 | 3 | 24 | 2,30 | 25 | 2,24 | 27 | 2,13,20 | 30 | 2 | 32 | 1,52,30 | 36 | 1,40 | 40 | 1,30 |
| 45 | 1,20 | 48 | 1,15 | 50 | 1,12 | 54 | 1,6,40 | 60 | 1 | 1,4 | 56,15 | 1,12 | 50 | 1,15 | 48 | 1,20 | 45 | 1,21 | 44,26,40 |
Aus einer Reziprokentabelle lässt sich viel ablesen, u. a. oder oder , aber auch umgekehrt ist usw.
Beispiele von Divisionen:
- .
- .
Wurzelberechnung
Der antike griechische Mathematiker und Ingenieur Heron von Alexandria verwandte in seinen Metrica zur Wurzelberechnung die schon im altbabylonischen Reich bekannte Methode[8]
- .
entnahm man dazu aus einer Quadratzahltabelle. Für die (irrationale) Quadratwurzel von 2 ergibt sich so:
- ,
d. h.
- .
Auf einer babylonischen Tontafel (Yale Babylonian Collection 7289) findet sich aber auch noch ein besserer Näherungswert auf der Diagonalen eines Quadrates:
- .
Wegen
- ,
liegt zwischen 1;25 und 1;24,42,21 deren arithmetisches Mittel
näher bei
- .
Nun werden die Seitenlänge des Quadrats auf der Tontafel mit 30 und die Länge der Diagonalen mit 42,25,35 angegeben, was sich als folgende Rechnung deuten lässt:
- .
Das Beispiel zeigt, dass die Babylonier algebraische und geometrische Kenntnisse hatten (hier könnte der „Satz des Pythagoras“ benutzt worden sein).
Ein- und zweihändiges Zählen mit Fingergliedern und Fingern
Im gewohnten Dezimalsystem (Zehner-System) zählt man mit den zehn Fingern (2 × 5) beider Hände. In einigen Gegenden der Welt existierte aber ein Zählen mit Hilfe der Fingerglieder, das einhändig zur Zahl zwölf (duodezimal), zweihändig aber zur Zahl 60 führte.[9] Trotzdem ist hier zu beachten, dass das zweihändige Zählen mit Fingergliedern nach dem Prinzip 5 × 12 funktioniert und nicht wie das Sexagesimale Zahlensystem nach dem Prinzip 6 × 10.
Einhändiges Zählen bis 12

Grundprinzip: 4 × 3 = 12
Gezählt wird mit dem Daumen als Zeiger und den Fingergliedern der gleichen Hand als Zählobjekt.
- Das einhändige Zählen beginnt, indem man für das erste Objekt mit dem Daumen die Spitze, also das obere Fingerglied, des kleinen Fingers der gleichen Hand berührt.
- Für das zweite Objekt wird mit dem Daumen das mittlere Fingerglied des kleinen Fingers berührt; so zählt man mit dem Daumen glied- und fingerweise weiter.
- Drei → unteres Glied des kleinen Fingers
- Vier → oberes Glied des Ringfingers
- Fünf → mittleres Glied des Ringfingers
- Sechs → unteres Glied des Ringfingers
- Sieben → oberes Glied des Mittelfingers
- Acht → mittleres Glied des Mittelfingers
- Neun → unteres Glied des Mittelfingers
- Zehn → oberes Glied des Zeigefingers
- Elf → mittleres Glied des Zeigefingers
- Zwölf → unteres Glied des Zeigefingers
Mit anderen Worten: vier Finger mit je 3 Fingergliedern ergibt 12.
Zweihändiges Zählen bis 60
Grundprinzip: 5 × 12 = 60
Nachdem mit Hilfe des Daumens als Zeiger mit den jeweils drei Fingergliedern der restlichen vier Finger der gleichen Hand (4 × 3 = 12) das erste Dutzend abgezählt ist, ist die Zählkapazität einer Hand zunächst erschöpft.
- Die zweite Hand war bis jetzt zur Faust geballt. Um sich zu merken, dass ein Dutzend gezählt wurde, streckt man nun einen Finger, z. B. den Daumen aus.
- Nun zählt man weiter, indem man mit der ersten Hand wieder bei eins beginnt. Bei zwölf angekommen, ist das zweite Dutzend voll.
- Um sich zu merken, dass zwei Dutzend gezählt wurden, streckt man nun den nächsten Finger der zweiten Hand, z. B. nach dem Daumen den Zeigefinger aus.
- Mit den fünf Fingern der zweiten Hand kann man so fünfmal ein Dutzend der ersten Hand abzählen, also 5 × 12 = 60.
- (Nun kann man noch einmal mit der ersten Hand das nächste Dutzend zählen, also mit zwei Händen bis 72 (5 × 12 + 12), also 60 gemerkt an der zweiten Hand plus 12 an der ersten Hand.)
Dieses Fingerzählsystem existiert noch in Teilen der Türkei, des Irak, in Indien und Indochina.
Es kann auch bis 12 × 12 = 144 (ein Gros) bzw. 156 (12 × 12 + 12) gezählt werden, indem mit der zweiten Hand ebenfalls das Zählen mit Fingergliedern betrieben wird.
Zweihändiges Zählen mit zweitem Helfer bis 3600
Grundprinzip: 10 × 60 = 600; bzw. 60 × 60 = 3600
Beim Zählen einer größeren Menge kann auf ein Hilfsmittel zurückgegriffen werden, etwa Stöcke, Steine, Striche oder die zehn Finger eines Helfers. Jeweils fünf Dutzend, also 60, werden mit einem der Hilfsmittel gemerkt. Mit den zehn Fingern eines menschlichen Helfers kann bis 10 × 60 = 600 gezählt werden, bzw. wenn der Helfer ebenfalls das 60er-Fingerzählsystem anwendet, dann sogar bis 60 × 60 = 3600 und mit den anderen Hilfsmitteln auch noch weiter.
Literatur
- Robert Kaplan: Die Geschichte der Null. Gebundene Ausgabe: Campus Verlag, Frankfurt am Main 2000, ISBN 3-593-36427-1.
- Taschenbuchausgabe: Piper Verlag, München 2003, ISBN 3-492-23918-8.
- Richard Mankiewicz: Zeitreise der Mathematik – Vom Ursprung der Zahlen bis zur Chaostheorie. VGS Verlagsgesellschaft, Köln 2000, ISBN 3-8025-1440-8.
- Kurt Vogel: Vorgriechische Mathematik. Teil II: Die Mathematik der Babylonier. Schroedel, Hannover und Schöningh, Paderborn 1959.
Weblinks
- Christoph Grandt: Das Babylonische Sexagesimalsystem. (PDF; 215 kB)
Einzelnachweise
- ↑ J. P. McEvoy: Sonnenfinsternis. Berlin-Verlag, 2001, S. 43. K. Vogel: Teil II, S. 22 f.
- ↑ K. Vogel: Vorgriechische Mathematik. Teil I: Vorgeschichte und Ägypten. Schroedel, Hannover, und Schöningh, Paderborn 1958. S. 16, Abb. 11.
- ↑ K. Vogel: Teil II, S. 23.
- ↑ Ifrah: Universalgeschichte der Zahlen. 2. Auflage. Campus, Frankfurt am Main und New York 1997, ISBN 3-593-34192-1, Das Sexagesimalsystem, S. 69 ff. (Erstausgabe: 1991).
- ↑ Thureau-Thangin nannte 1932 das eine „vigesimale Insel innerhalb des sumerischen Zahlensystems“. Ifrah: Universalgeschichte der Zahlen. 2. Auflage. S. 71.
- ↑ Rik Verhulst; Im Banne der Mathematik: Die kulturellen Aspekte der Mathematik in Zivilisation, Kunst und Natur. Springer, 2019, S. 194.
- ↑ K. Vogel: Teil II, S. 18 f.
- ↑ K. Vogel, Teil II, S. 34 f.
- ↑ Georges Ifrah: Universalgeschichte der Zahlen. Lizenzausgabe Zweitausendundeins Auflage. Campus, Frankfurt am Main 1993, ISBN 3-86150-704-8, Das Sexagesimalsystem, S. 69–75 u. 90–92 (französisch: Histoire universelle des chiffres. Übersetzt von Alexander von Platen).


























