Rekonstruktionsfilter
In der Signalverarbeitung ist ein Rekonstruktionsfilter ein Filter, das bestimmt, wie bei der Umwandlung eines diskreten in ein kontinuierliches Signal die einzelnen Abtastwerte interpoliert werden sollen.
Bei gleichmäßiger Abtastung über der Nyquist-Frequenz ist die Sinc-Funktion das theoretisch ideale Rekonstruktionsfilter, da ihre Fourier-Transformation eine Rechteckfunktion (idealer Tiefpass) ist, die im Frequenzbereich das Nutzsignal vollständig isoliert. Das Originalsignal kann somit vollständig wiederhergestellt werden.
In der Elektronik wird ein Rekonstruktionsfilter auf das Ausgangssignal eines Digital-Analog-Umsetzers angewandt.
Rekonstruktionsfilter in der Computergrafik
In der Computergrafik wird nicht zwischen Rekonstruktionsfiltern und Antialiasing-Filtern unterschieden. Statt ein kontinuierliches Signal zu erzeugen, wird die Farbe eines Pixels aus in der Nähe des Pixels ermittelten Farbwerten berechnet, zum Beispiel bei der Skalierung von Bildern oder um Antialiasing anzuwenden. Das dabei verwendete Rekonstruktionsfilter ist eine zweidimensionale Funktion oder Distribution, die über dem zu berechnenden Pixel zentriert ist. Da in der Computergrafik die abzutastende Bildbeschreibung aufgrund von Objektkanten fast immer höhere Frequenzen enthält, als durch Abtastung erfasst werden können, ist das Tiefpassfilter (Sinc-Filter) nicht ideal.
Konstruktion zweidimensionaler Filter
Beim Vergleich unterschiedlicher Rekonstruktionsfilter können zunächst die eindimensionalen Filter betrachtet werden. Es gibt zwei Möglichkeiten, wie aus einem eindimensionalen Rekonstruktionsfilter ein zweidimensionales erzeugt werden kann, nämlich durch radiale Symmetrie und durch Separation.
Bei der Konstruktion durch radiale Symmetrie wird ein zweidimensionales Rekonstruktionsfilter aus der Rotationsfläche eines eindimensionalen Filters erzeugt. Dabei hängt der Filterwert alleine von der Entfernung vom Mittelpunkt des Filters ab. Um radial symmetrische Rekonstruktionsfilter anzuwenden, muss daher der euklidische Abstand zu den Abtastwerten berechnet werden.
Bei der Konstruktion durch Separation wird ein zweidimensionales Rekonstruktionsfilter erzeugt, indem das eindimensionale Filter über die X- beziehungsweise Y-Achse verschoben und das Produkt aus beiden so erzeugten Funktionen gebildet wird. Die so erzeugten separablen Filter eignen sich gut für rasterförmig angeordnete Abtastwerte. In diesem Fall kann die Berechnung des Filterwertes durch eine Reihe von Interpolationen mit dem entsprechenden eindimensionalen Rekonstruktionsfilter ersetzt werden. Hierbei wird zunächst in einem Zwischenschritt für jede der vom Filter überlappten Abtastpunkte der Wert des eindimensionalen Filters an der x-Koordinate des Filtermittelpunktes berechnet. Anschließend wird aus den so erzeugten vertikalen Punkten der Wert am Filtermittelpunkt berechnet.
Separable Filter führen zu anisotropen Effekten: Bildartefakte, die durch separable Filter entstehen, sind nicht isotrop (in alle Richtungen gleichmäßig) verteilt, sondern bevorzugt entlang der Filter-Konstruktionsachsen (also horizontal und vertikal) ausgerichtet.
Da bei separablen Filtern nur eine Folge von eindimensionalen Interpolationen durchgeführt werden muss und keine euklidischen Abstände berechnet werden, sind sie schneller zu berechnen als radial symmetrische Filter.
Das Gauß-Filter ist das einzige radial symmetrische Rekonstruktionsfilter, das zugleich separabel ist. Bei allen anderen Filtern führt die separable und die radial symmetrische Erzeugung zu unterschiedlichen Ergebnissen.
Bekannte Filter
Die folgende Tabelle listet Rekonstruktionsfilter auf, die in der Computergrafik häufig beschrieben oder verwendet werden.
| Filterfunktion | Beschreibung | Beispielbilder | |
|---|---|---|---|
| Schachbrett | Zonenplatte | ||
|
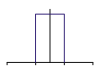
Box-Filter. Beim Box-Filter haben alle Abtastwerte innerhalb eines um das Pixel gelegte Quadrat (meist mit der Kantenlänge von einem Pixelabstand) die gleiche Gewichtung. Das Box-Filter liefert im Allgemeinen schlechte Ergebnisse, da seine Fourier-Transformierte eine Sinc-Funktion ist, die den gewünschten Frequenzbereich nur schlecht isoliert. | 
|

|

|
Kegelfilter. Beim Kegelfilter fällt die Gewichtung mit zunehmender Distanz zum Pixel ab. Es liefert etwas bessere Ergebnisse als das Box-Filter. | 
|

|

|
Sinc-Filter. Das Sinc-Filter ist zwar theoretisch ideal, doch gilt dies nur bei gleichmäßiger Abtastung über der Nyquist-Frequenz, was in der Computergrafik meist nicht gegeben ist. Besonders bei Kanten führt der Sinc-Filter zu starken Ringing-Artefakten. Außerdem hat die Sinc-Funktion einen unendlichen Träger, sodass zur Berechnung des Farbwerts eines Pixels alle Abtastwerte des Bildes herangezogen werden müssen. Ein einfaches Abschneiden der Sinc-Funktion führt zu schlechten Ergebnissen. | ||
|
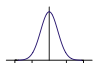
Gauß-Filter. Beim Gauß-Filter wird zur Rekonstruktion eine Gauß-Funktion verwendet. Dieses Filter führt zu Unschärfe, dafür werden aber Alias-Effekte gut unterdrückt. | 
|

|
 Parameterwahl B=C=⅓ |
Mitchell-Netravali-Filter. Die Mitchell-Netravali-Filter sind stückweise kubische Filter mit vier Pixel breiten Trägern. Sie sind durch zwei freie Parameter änderbar und wurden speziell dafür entworfen, die aus Rekonstruktionsfiltern resultierenden Artefakte zu untersuchen. Bei geeigneter Parameterwahl liefern die Filter einen guten Kompromiss zwischen Unschärfe, Anisotropie und Ringing. Die Mitchell-Netravali-Filter werden auch als bikubische Filter bezeichnet; Spezialfälle sind kubische B-Splines, Cardinal Splines und Catmull-Rom Splines. | 
|

|
 Parameterwahl a=3 (Filter abgeschnitten nach drei Pixeln) |
Lanczos-Filter. Das Lanczos-Filter basiert auf der Sinc-Funktion, die nach typischerweise zwei oder drei Pixeln abgeschnitten und mit einer Fensterfunktion multipliziert wurde, um eine allmähliche Abnahme zu gewährleisten. Es führt zu weniger Ringing-Artefakten als das Sinc-Filter. | 
|

|
Ungleichmäßige Abtastung
Da Bildbeschreibungen in der Computergrafik ein unbegrenztes Frequenzspektrum aufweisen können, wird im Allgemeinen eine ungleichmäßige Abtastung vorgezogen, sodass Alias-Effekte durch Rauschen ersetzt werden. Für ungleichmäßige Abtastverfahren, die zudem auf ein Signal mit unbegrenztem Frequenzspektrum angewandt werden, gibt es kein ideales Rekonstruktionsverfahren. Die neuere Forschung in der Signalverarbeitung geht davon aus, dass in solchen Fällen eine perfekte Rekonstruktion in der Praxis nicht möglich ist. Stattdessen wird versucht, die Abweichung zwischen dem Originalsignal und dem rekonstruierten Signal zu minimieren, und zwar unabhängig davon, ob das Originalsignal ein unbegrenztes Frequenzspektrum aufweist oder nicht.[1] Diese theoretischen Erkenntnisse werden jedoch bisher kaum angewandt.
Artefakte bei der Rekonstruktion
Rekonstruktionsfilter können neben Postaliasing zu einer Reihe von weiteren Artefakten führen:[2][3]
- Abtastfrequenz-Welligkeit entsteht, wenn gleiche Abtastwerte zu einem nicht-konstanten rekonstruierten Signal führen.
- Anisotropische Effekte entstehen, wenn der Rekonstruktionsfilter nicht radial symmetrisch ist.
- Ringing (Gibbssches Phänomen) bezeichnet Über- oder Unterschwinger an harten Kanten.
- Unschärfe.
Literatur
- Matt Pharr, Greg Humphreys: Physically Based Rendering. From Theory to Implementation, S. 279–367. Morgan Kaufmann, London 2004, ISBN 0-12-553180-X (PDF, 7 MB)
- Ken Turkowski, Steve Gabriel: Filters for Common Resampling Tasks. In Andrew Glassner: Graphics Gems I, S. 147–165. Academic Press, Boston 1990, ISBN 0-12-286165-5 (PDF, 160 kB)
Einzelnachweise
- ↑ Matt Pharr, Greg Humphreys: Physically Based Rendering. From Theory to Implementation, S. 350 f.
- ↑ William Schreiber, Donald Troxel: Transformation Between Continuous and Discrete Representations of Images: A Perceptual Approach. IEEE Transactions on Pattern Analysis and Machine Intelligence 7,2 (Mar. 1985): 178–187, ISSN 0018-9340. Zitiert in Don Mitchell, Arun Netravali: Reconstruction Filters in Computer Graphics
- ↑ Stephen Marschner, Richard Lobb: An Evaluation of Reconstruction Filters for Volume Rendering. In Proceedings of the conference on Visualization ’94, S. 100–107. IEEE Computer Society Press, Los Alamitos 1994, ISBN 0-7803-2521-4 (Online)
