Die Kinetik ist ein Teilbereich der physikalischen Chemie, der in Makrokinetik und molekulare Kinetik unterteilt wird. Die molekulare Kinetik behandelt den zeitlichen Ablauf von chemischen Reaktionen auf der molekularen Ebene und schließt die Mikrokinetik ein, welche sich mit der Kinetik von Elementarreaktionen beschäftigt.^[1] Die Makrokinetik betrachtet den Einfluss makroskopischer Wärme- und Stofftransportprozesse auf die Kinetik chemischer Reaktionen und stellt damit das Bindeglied zwischen Reaktionskinetik und chemischer Reaktionstechnik dar. Dieser Artikel beschäftigt sich mit der molekularen Kinetik chemischer Reaktionen. Die Kinetik elektrochemischer Prozesse wird im Artikel elektrochemische Kinetik behandelt.

Die grundlegende Größe der Kinetik ist die Reaktionsgeschwindigkeit (englisch rate of reaction) mit der Dimension Stoffmenge pro Zeit und Volumen.^[1][2][3][4] Die aus den Basisgrößen des internationalen Einheitensystems abgeleitete Einheit der Reaktionsgeschwindigkeit ist Mol pro Kubikmeter und Sekunde. Die Reaktionsgeschwindigkeit gibt die Änderung der Umsatzvariable (Menge der Reaktionsereignisse, die durch die Reaktionsgleichung der betrachteten Reaktion definiert werden, in mol) pro Zeit- und Volumeneinheit unter isochoren Bedingungen, also bei konstantem Volumen, an.^[1] Isochore Bedingungen liegen unter anderem bei solvothermalen Reaktionen und Reaktionen, die in Autoklaven durchgeführt werden, vor.

Sind die stöchiometrische Zahl und der Betrag der stöchiometrischen Zahl eines an der betrachteten Reaktion beteiligten Stoffes , wird für eine Reaktion

die Reaktionsgeschwindigkeit gleich:

Hierbei sind die Reaktionsdauer, das Reaktionsvolumen und , , sowie die volumenbezogenen Stoffmengenkonzentrationen der an der betrachteten Reaktion beteiligten Stoffe , , und . Alternativ kann auch mit Hilfe der Stoffmengen , , und der Stoffe , , und formuliert werden. Mit , , und erhält man:

Der Differentialquotient ist gleich der Steigung des zugrundeliegenden Konzentrations-Zeit-Profils , welches als Funktion von darstellt. Da als Ausgangsstoff verbraucht wird, sind die differentielle Konzentrationsänderung und damit der Differentialquotient negativ. Da auch die stöchiometrische Zahl eines Ausgangsstoffes konventionsgemäß ein negatives Vorzeichen hat, werden der Ausdruck und somit die Reaktionsgeschwindigkeit positiv.

Finden Reaktionen im Batchbetrieb unter nicht-isochoren Bedingungen statt, ist das Volumen der Reaktionsmischung veränderlich. Dies muss bei der Formulierung von Geschwindigkeitsgesetzen berücksichtigt werden.^[1][5] Die Stoffmenge eines an der betrachteten Reaktion beteiligten Stoffes ist gleich:

Ist variabel, erhält man die Änderung von durch Differenzieren nach und :

Für die Reaktionsgeschwindigkeit erhält man entsprechend:^[1][5]

Ausklammern von ergibt:

Dieser Ausdruck kann unter Anwendung der Produktregel weiter umgeformt werden:

Werden Reaktionen im Fließbetrieb betrachtet, wird die Reaktionsdauer durch die statistische Verweilzeit ersetzt. Weiterhin wird das Volumen durch den Volumenstrom ersetzt, wobei gilt:

Man erhält entsprechend:^[5]

In der Praxis wird für Reaktionen, die isobar (Druck konstant) und isotherm (Temperatur konstant) in Lösung durchgeführt werden, häufig angenommen, dass diese näherungsweise auch isochor verlaufen, Volumenänderungen also vernachlässigbar sind. Damit kann die Reaktionskinetik mit dem wesentlich einfacheren Formalismus für isochore Prozesse beschrieben werden.

Für die Erstellung einer integralen Stoffmengenbilanz für volumenveränderliche Reaktionen wird in der Literatur^[6][7] das Volumen in der bisherigen (volumenkonstanten) Stoffmengenbilanz durch einen der nachfolgend genannten Ansätze substituiert:

(für eine einfache Hinreaktion)

oder

(für eine komplexe Reaktion)

In den genannten Volumenbilanzen ist das konstante Anfangsvolumen (oder der Anfangsvolumenstrom), ist der Umsatz, ist die Umsatzvariable (Fortschreitungsgrad) und ein Modellfaktor (Proportionalitätskonstante). In sind die stöchiometrischen Koeffizienten der beteiligten Reaktanden und deren molare Volumina (stoffmengenspezifische Volumen) enthalten.^[6] Epsilon wird auch als „Koeffizient der Volumenänderung durch Reaktion“ betitelt.

Laufen gleichzeitig mehrere komplexe Reaktionen ab, so ist anzusetzen:

(für n komplexe Reaktionen)

Die Koeffizienten können aus der Dichteänderung (Volumenänderung) des Reaktionsgemisches bestimmt werden. Je nach Richtung der Volumenänderung/Dichteänderung können sie positive oder negative Werte haben. Bei einfachen Einzelreaktionen kann der Koeffizient Epsilon nach folgender Formel bestimmt werden:

Hier ist X der Umsatz (Umsatzgrad) und die Dichte (Massendichte) bzw. Anfangsdichte^[8]. (Hinweis: Die vorstehende Formel – angegeben wie in der zitierten Quelle – ist physikalisch nicht ganz korrekt, denn der Volumenquotient muss dem Kehrwert des Dichtequotienten entsprechen. Insofern liefern linker und rechter Teil der Formel für einen einzigen Fall unterschiedliche Vorzeichen für Epsilon.)

Die Abhängigkeit der Reaktionsgeschwindigkeit von den aktuellen Konzentrationen der Reaktanten einer Reaktion wird empirisch durch Geschwindigkeitsgesetze beschrieben, in der Regel Produkte von Konzentrationen der Edukte mit einer Geschwindigkeitskonstanten .

Phänomenologisch beobachtbare Bruttoreaktionen können komplexe Reaktionsmechanismen aufweisen, die Sequenzen aus mehreren reversiblen Elementarreaktionen umfassen. Beispiele hierfür sind Reaktionen, die dem Lindemann-Mechanismus folgen, Kettenreaktionen oder durch die Michaelis-Menten-Theorie beschreibbare enzymkatalysierte Reaktionen. Weiterhin kann die beobachtbare Reaktionsgeschwindigkeit durch Konkurrenzreaktionen beeinflusst werden. Im Falle von radikalischen Polymerisationsreaktionen kann bei hohen Umsätzen eine als Trommsdorff-Effekt bekannte Selbsbeschleunigung eintreten. Die bei hohen Umsätzen und damit hohen Polymerisationsgraden erhöhte Viskosität der Reaktionsmischung führt zu einer erheblichen Verringerung der Wahrscheinlichkeit für Kettenabbruchreaktionen durch Rekombination von Kettenenden, während sich die exotherme, die Anlagerung von Monomeren an die Kettenenden umfassende Kettenwachstumsreaktion aufgrund der größer werdenden Zahl von aktiven Kettenenden beschleunigt. Die dadurch eintretende Temperaturerhöhung in der Reaktionsmischung verstärkt wiederum die Beschleunigung der Kettenwachstumsreaktion.

Da Geschwindigkeitsgesetze meist komplexe Reaktionsgeschehen abbilden, kann aus diesen nicht unmittelbar auf den Reaktionsmechanismus geschlossen werden. In manchen Fällen hilft der Isotopeneffekt bei der Aufklärung des Mechanismus. Häufig werden Geschwindigkeitsgesetze auf der Basis von vereinfachten Reaktionsmodellen formuliert.^[9] So kann die Kinetik von zusammengesetzten Reaktionen, die mehrere konsekutive Elementarreaktionen umfassen, von einer besonders langsam ablaufenden Elementarreaktion als geschwindigkeitsbestimmendem Schritt dominiert sein. In diesem Fall wird die Kinetik der zusammengesetzten Reaktion oft in zufriedenstellender Weise durch die einfachere Kinetik der besonders langsam ablaufenden Elementarreaktion repräsentiert. Treten im Verlauf von Reaktionen reaktive Intermediate auf, kann das Bodensteinsche Quasistationaritätsprinzip angewendet werden.

Zeitgesetze geben die Umsatzvariable einer Bruttoreaktion oder die Konzentration eines daran beteiligten Stoffes als Funktion der Reaktionsdauer an. In einigen Fällen lassen sich Zeitgesetze aus den jeweiligen Geschwindigkeitsgesetzen durch Variablentrennung und Integration ermitteln bzw. umgekehrt durch Ableiten.

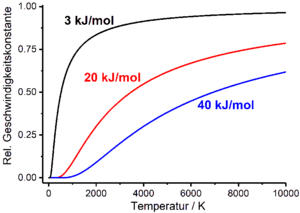
Reaktionsgeschwindigkeiten hängen grundsätzlich von den Zustandsgrößen ab, die das reagierende System kennzeichnen, wie etwa der Temperatur , dem Druck und dem Volumen. In die Geschwindigkeitsgesetze chemischer Prozesse findet diese Abhängigkeit über die Geschwindigkeitskonstante beziehungsweise die Halbwertszeit Eingang, die ihrerseits Funktionen von Temperatur, Druck und Volumen sind. In der Praxis relevant ist vor allem die Temperaturabhängigkeit der Reaktionsgeschwindigkeit. Diese wird empirisch durch die Arrhenius-Gleichung beschrieben, die die Geschwindigkeitskonstante in Beziehung zur Temperatur setzt. Die Arrhenius-Gleichung ist eine Exponentialfunktion, welche einen präexponentiellen Faktor mit der Dimension der Geschwindigkeitskonstante und die molare Aktivierungsenergie im Exponenten als empirische Parameter enthält ( ist die allgemeine Gaskonstante).

Der Geschwindigkeitskoeffizient k ist in erster Linie von der Temperatur abhängig (in Sonderfällen auch vom Druck). Der Temperatureinfluss auf den Geschwindigkeitskoeffizienten wird durch den erweiterten Ansatz von Arrhenius recht gut wiedergegeben:^[10]

Analog kann mittels der Arrhenius-Gleichung auch dargestellt werden, wie Halbwertszeiten von der Temperatur abhängen. Die Arrhenius-Gleichung hat dann einen Exponenten mit positivem Vorzeichen und der präexpoentielle Faktor die Dimension Zeit:

Geht man näherungsweise davon aus, dass der präexponentielle Faktor und die Aktivierungsenergie unabhängig von der Temperatur sind, läuft die Geschwindigkeitskonstante gegen null, wenn die Temperatur gegen null läuft, und gegen den präexponentiellen Faktor, wenn die Temperatur gegen unendlich läuft. Bei dieser großen Variation der Temperatur ist allerdings die Temperaturabhängigkeit der Stoßzahl zu berücksichtigen, empirisch oft durch^[11]

Im Verlauf eines elementaren Reaktionsereignisses wird vom reagierenden System eine Trajektorie auf einer Potentialhyperfläche durchlaufen, die durch sukzessive strukturelle Änderungen wie Änderungen von Bindungswinkeln und Bindungslängen gekennzeichnet ist. Gemäß der Theorie des Übergangszustandes wird dabei ein Ausgangsstoffe und Produkte trennender Potentialwall (Aktivierungsbarriere) überwunden, der einen Sattelpunkt auf der Potentialhyperfläche darstellt. Die Zustände, die das reagierende System während der betrachteten Elementarreaktion durchläuft, werden am zweckmäßigsten durch das jeweils anzuwendende thermodynamische Potential beschrieben, welches die durch Veränderungen im reagierenden System hervorgerufenen Entropieänderungen im Universum abbildet. Werden Druck und Temperatur konstant gehalten, ist dies die freie Enthalpie. Der Sattelpunkt ist der Ort der höchsten freien Enthalpie, den das reagierende System im Verlauf eines elementaren Reaktionsereignisses durchläuft. Der Zustand, den dass reagierende System beim Durchlaufen des Sattelpunktes einnimmt, wird als Übergangszustand bezeichnet. Die molare freie Aktivierungsenthalpie repräsentiert die Höhe der für die Umwandlung der Ausgangsstoffe in die Produkte zu überwindenden Potentialbarriere, also die Differenz der freien Enthalpien des Übergangszustandes und des Ausgangszustandes vor Beginn des elementaren Reaktionsereignisses. Die Größe der Geschwindigkeitskonststante , die die Kinetik der Umwandlung der Ausgangsstoffe in die Produkte repräsentiert, hängt von ab (siehe Abschnitt „Thermodynamische Formulierung“ im Artikel „Theorie des Übergangszustandes“):

Entsprechend gilt für die Abhängigkeit der Geschwindigkeitskonststante der Rückreaktion von deren molarer freier Aktivierungsenthalpie :

Viele Reaktionen sind Gleichgewichtsreaktionen, bei denen neben der Bildung von Reaktionsprodukten durch die Hinreaktion durch die Rückreaktion auch Ausgangsstoffe aus den Reaktionsprodukten neu gebildet werden:

Sofern die Hinreaktion mit der molaren freien Aktivierungsenthalpie sowie der molaren freien Reaktionsenthalpie

und die Rückreaktion mit der molaren freien Aktivierungsenthalpie

exakt entlang derselben Reaktionstrajektorie in jeweils entgegensetzter Richtung ablaufen, gilt für die molare freie Aktivierungsenthalpie der Hinreaktion:

Die Geschwindigkeitskonstante der Hinreaktion wird dann:

Für den Quotienten aus k_hin und k_rueck folgt:

Vereinfachung ergibt:

Somit wird:

Dabei ist die thermodynamische Gleichgewichtskonstante der betrachteten Reaktion. Die Geschwindigkeitskonstanten der Hinreaktion und der Rückreaktion sind somit durch miteinander gekoppelt ‒ das Verhältnis wird durch die thermodynamische Gleichgewichtskonstante bestimmt. Dieser Zusammenhang wird oft dahingehend fehlinterpretiert, dass die Gleichgewichtskonstante einer Gleichgewichtsreaktion von den Geschwindigkeitskonstanten der Hin- und Rückreaktionen abhinge. Diese Vorstellung beruht jedoch auf einem unzutreffenden Präkonzept. Thermodynamische Größen, die wie die freie Reaktionsenthalpie und die Gleichgewichtskonstante Zustandsänderungen beschreiben, hängen ausschließlich von Ausgangs- und Endzustand ab, nicht jedoch vom Weg, auf dem sich das System vom Ausgangs- zum Endzustand bewegt.

Die Existenz von Potentialbarrieren, die im Verlauf einer phänomenologisch beobachtbaren Bruttoreaktion bei der Umwandlung der Ausgangsstoffe in die Produkte überwunden werden müssen, wird empirisch durch die Arrhenius-Gleichung abgebildet. Im Gegensatz zur aus der Theorie des Übergangszustandes resultierenden Eyring-Gleichung berücksichtigt die Arrhenius-Gleichung dabei weder die Zahl noch die Natur der vom reagierenden System zu durchlaufenden Übergangszustände, sondern repräsentiert die zu überwindenden Potentialbarrieren durch den phänomenologischen Parameter Aktivierungsenergie . Läuft die Aktivierungsenergie bei konstanter Temperatur gegen unendlich, konvergiert die Geschwindigkeitskonstante gemäß der Arrhenius-Gleichung gegen null. Ist die Aktivierungsenergie gleich null, wird die Geschwindigkeitskonstante gleich dem präexponentiellen Faktor . Analog kann mittels der Arrhenius-Gleichung auch dargestellt werden, wie Halbwertszeiten von der Aktivierungsenergie abhängen. Läuft die Aktivierungsenergie bei konstanter Temperatur gegen unendlich, läuft auch die Halbwertszeit gegen unendlich. Ist die Aktivierungsenergie null, wird die Halbwertszeit gleich dem präexponentiellen Faktor .

Allgemein erhöht sich bei konstanter Temperatur die Reaktionsgeschwindigkeit, wenn die Aktivierungsenergie reduziert wird. Bei der Katalyse chemischer Reaktionen werden daher alternative Reaktionstrajektorien bereitgestellt, die zu einer Verringerung der Aktivierungsenergie führen. Damit werden höhere Reaktionsgeschwindigkeiten erreicht, ohne hierfür die Reaktionstemperatur erhöhen zu müssen.

Werden für eine Reaktion bei mehreren Temperaturen Konzentrations-Zeit-Profile und aus diesen die jeweiligen Geschwindigkeitskonstanten experimentell bestimmt, lässt sich auch die Aktivierungsenergie ermitteln. Logarithmieren überführt die Arrhenius-Gleichung in eine Geradengleichung:

Die graphische Auftragung des natürlichen Logarithmus der experimentell ermittelten Geschwindigkeitskonstanten gegen ergibt eine Gerade, deren Steigung der negativen Aktivierungsenergie entspricht. Der Schnittpunkt der Geraden mit der -Achse ist der Logarithmus des präexponentiellen Faktors der Arrhenius-Gleichung.

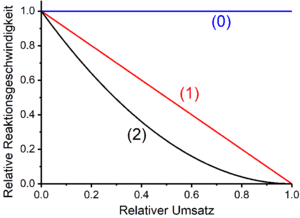
In vielen Fällen ist die Geschwindigkeit chemischer Reaktionen, an denen Ausgangsstoffe beteiligt sind, proportional zu Produkten von Potenzfunktionen der Konzentrationen der Ausgangsstoffe :

Hierbei ist die Geschwindigkeitskonstante. Die Exponenten sind die partiellen Reaktionsordnungen in Bezug auf die Ausgangsstoffe . Die Summe ist die Gesamtreaktionsordnung der betrachteten Reaktion. Partielle Reaktionsordnungen können, müssen aber nicht die gleichen Beträge wie die stöchiometrischen Zahlen der betreffenden Ausgangsstoffe einer Reaktion besitzen. Die in Bruttoreaktionsgleichungen auftretenden stöchiometrischen Zahlen der Ausgangsstoffe repräsentieren häufig die Gesamtstöchiometrie zusammengesetzter Reaktionen, die mehrere Elementarreaktionen umfassen. Partielle Reaktionsordnungen und damit die Gesamtreaktionsordnungen resultieren häufig, wie bei nukleophilen Substitutionen und Eliminierungen erster Ordnung, aus geschwindigkeitsbestimmenden Elementarreaktionen, deren Stöchiometrie sich jeweils von der Stöchiometrie der betrachteten Bruttoreaktion unterscheidet. Sofern eine Bruttoreaktion wie etwa bei radikalischen Kettenreaktionen sich überlagernde oder gekoppelte Elementarreaktionen umfasst, ohne dass eine langsame und damit geschwindigkeitsbestimmernde Elementarreaktion existiert, können sich die partiellen Reaktionsordnungen ebenso von den Stöchiometriezahlen der betreffenden Komponenten unterscheiden. In derartigen Fällen treten auch gebrochene Reaktionsordnungen auf.^[12][13]

Die Zeitgesetze der Reaktionen, deren Gesamtreaktionsordnung bestimmbar ist, lassen sich durch Umformungen in Geradengleichungen überführen (siehe Tabelle unten; für Reaktionen nullter Ordnung sind Konzentrations-Zeit-Profile immer linear). In dieser Form dargestellte Zeitgesetze können zur experimentellen Ermittlung der Gesamtreaktionsordnung mit nach verschiedenen Reaktonsdauern gemessenen Konzentrationen eines Reaktanten verglichen werden. Der Betrag der Steigung der so erhaltenen Geraden entspricht dem Produkt aus der Stöchiometriezahl des Ausgangsstoffes und der Geschwindigkeitskonstante .

Zeitgesetze, die linearisierten Auftragungen der Zeitgesetze zur Bestimmung der Geschwindigkeitskonstante sowie die Ausdrücke für die Halbwertszeiten sind für Reaktionen mit Geschwindigkeitsgesetzen des Typs in nachfolgender Tabelle unter Berücksichtigung der Stöchiometriezahl von Ausgangsstoff zusammengefasst.^[14][15] Zu beachten ist, dass ein negatives Vorzeichen hat. Die Einheiten der Geschwindigkeitskonstanten sind für alle Reaktionen mit der Gesamtreaktionsordnung gültig.

	0. Ordnung	1. Ordnung	2. Ordnung	n. Ordnung ()
Geschwindigkeitsgesetz
Zeitgesetz
Einheit
Lineare Auftragung des Zeitgesetzes	vs. t	vs. t	vs. t	vs. t
Halbwertszeit

Die Geschwindigkeit von Reaktionen nullter Ordnung ist unabhängig von den Konzentrationen der Reaktanten. Dadurch ist die Reaktionsgeschwindigkeit konstant. Zeitgesetze nehmen demzufolge die Form einer Geraden mit negativer Steigung (für Umsatzvariable und Reaktanten) oder mit positiver Steigung (für Produkte) an. Die Geradensteigung entspricht dem Betrag der Geschwindigkeitskonstante k. Beispiele für Reaktionen nullter Ordnung sind bestimmte photochemische und katalytische Reaktionen. So ist beispielsweise die biologische Oxidation von Ethanol zu Acetaldehyd durch bestimmte Alkoholdehydrogenasen nullter Ordnung in Bezug auf Ethanol.^[16] Ein weiteres Beispiel ist die Emulsionspolymerisation, bei der nach der Phase der Initiierung die Reaktion 0. Ordnung ist.^[17]

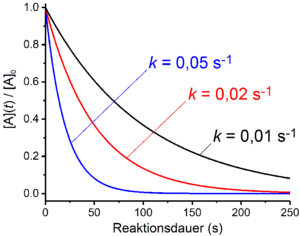
Bei Reaktionen erster Ordnung hängt die Reaktionsgeschwindigkeit linear von der Konzentration eines Reaktanden A ab. Dies ist der Fall, wenn der Gesamtprozess lediglich eine unimolekulare Zerfallsreaktion umfasst. Ein Beispiel hierfür ist der radioaktive Zerfall. Weiterhin sind Reaktionen, die mehrere Elementarreaktionen umfassen, erster Ordnung, wenn der geschwindigkeitsbestimmende Schritt ein Zerfalls- oder Dissoziationsprozess ist. Beispiele hierfür sind der S_N1-Mechanismus der nukleophilen Substitution oder der E1-Mechanismus bei Eliminierungsreaktionen. Das Geschwindigkeitsgesetz nimmt für eine Reaktion erster Ordnung folgende Form an:

Das Zeitgesetz erster Ordnung wird erhalten, indem zunächst die Variablen getrennt werden:

Im nächsten Schritt berechnet man die bestimmten Integrale:

Man erhält zunächst unter Berücksichtigung der Tatsache, dass die Stammfunktion zu ist:

Anwendung der Logarithmusregeln ergibt:

Umformen ergibt:

Entlogarithmieren ergibt das Zeitgesetz für Reaktionen erster Ordnung:

Beziehungsweise:

Sofern, wie es bei Reaktionen erster Ordnung häufig der Fall ist, gilt

,

wird das Zeitgesetz für Reaktionen erster Ordnung:

Zweiter Ordnung sind Elementarreaktionen, die auf bimolekularen Stößen beruhen. Beispiele hierfür sind nukleophile Substitutionen nach dem S_N2-Mechanismus sowie Eliminierungen nach dem E2-Mechanismus. Werden im Verlauf einer mehrschrittigen Reaktion auch Zerfalls- oder Dissoziationsprozesse erster Ordnung durchlaufen, sind diese meist die geschwindigkeitsbestimmenden Schritte, so dass, wie etwa bei S_N1- und E1-Reaktionen, die Gesamtreaktion erster Ordnung ist.

Findet der bimolekulare Stoß unter Beteiligung zweier gleichartiger Teilchen der Species statt, ist der Betrag der stöchiometrischen Zahl des Ausgangsstoffes gleich zwei, und die Reaktionsgleichung hat die Form:

Die hieraus resultierenden Geschwindigkeits- und Zeitgesetze sowie der Ausdruck für die Halbwertszeit von sind in der Tabelle oben aufgeführt.

Sind am bimolekularen Stoß Teilchen zweier verschiedener Species und beteiligt und sind die Beträge der stöchiometrischen Zahlen und der Reaktanten und jeweils gleich eins, wird die Reaktionsgleichung:

Das Geschwindigkeitsgesetz wird entsprechend:

Als Zeitgesetz erhält man mit als Ausgangskonzentration des Reaktanten vor Reaktionsbeginn:^[18]

Damit eine Reaktion dritter Ordnung ist, muss diese einen trimolekularen Stoß als Elementarreaktion umfassen. Da trimolekulare Stöße eine geringe Wahrscheinlichkeit besitzen, sind Reaktionen dritter Ordnung selten. Das Auftreten von Reaktionen dritter Ordnung wurde etwa im Zusammenhang mit Rekombinationsreaktionen von Atomen und Radikalen des Typs

,

wobei M als Stoßpartner fungiert, sowie für Reaktionen von Stickstoffmonoxid mit Halogenen X und Sauerstoff gemäß

und

postuliert.^[19]

Betrachtet wird eine elementare Gleichgewichtsreaktion mit den Geschwindigkeitskonstanten und der Hin- bzw. Rückreaktion und den Anfangskonzentrationen und

Als elementare Reaktionen sind Hin- und Rückreaktion jeweils erster Ordnung, d. h., die Reaktionsraten sind proportional zu den Konzentrationen:

Die Änderungsraten der Konzentrationen gehorchen mithin der Differentialgleichung

und die Gleichgewichtsbedingung (Stationarität) lautet

Lösungen linearer Differentialgleichungen erster Ordnung sind Exponentialfunktionen. Mit den Konzentrationen in Einheiten der (konstanten) Gesamtkonzentration lautet ein geeigneter Ansatz

(aus der Gleichgewichtsbedingung).

Ein kann durch berücksichtigt werden.

Den Ansatz einsetzen in die Differentialgleichung liefert die Abklingkonstante

Experimentell wird die Kinetik chemischer Reaktionen durch die Ermittlung von Konzentrations-Zeit-Profilen mittels quantitativer analytischer Methoden untersucht. Hierfür stellt die analytische Chemie ein breites und sich durch den Fortschritt der instrumentellen Analytik sowie der Mikroreaktionstechnik kontinuierlich weiterentwickelndes Methodensprektrum zur Verfügung. Die zur Ermittlung der Konzentrations-Zeit-Profile gewählte Messgröße sollte quantitativ proportional zur Konzentration der beobachteten Komponenten sein. Häufig verwendete Methoden zur Ermittlung von Konzentrations-Zeit-Profilen sind unter anderem die Messung der Dielektrizitätskonstanten, des Brechungsindexes, der optischen Aktivität, der Fluoreszenz oder der Leitfähigkeit der Reaktionslösung, die Messung von Volumen- oder Druckänderungen, Kalorimetrie sowie Absorptions- und Emissionsspektroskopie und Lichtstreuung.

Die Messgröße kann dabei am Reaktionsgemisch selbst berührungsfrei und ohne Entnahme von Proben aus dem Reaktionsgemisch beobachtet werden. Diese Vorgehensweise ist vorteilhaft, da auf diese Weise Störungen des Reaktionsablaufs minimiert werden. Eine andere Vorgehensweise beruht darauf, dass der Reaktionsmischung regelmäßig und meist automatisiert Aliquote entnommen werden. Diese können zerstörungsfreien Analysemethoden unterzogen und danach wieder mit der Reaktionsmischung vereinigt werden. Ebenso können Analysemethoden angewendet werden, die mit der Konsumption der entnommenen Aliquote verbunden sind. Werden der Reaktionsmischung Aliquote entnommen, greift man stärker als bei berührungsfreien Verfahren in das Reaktonsgeschehen ein. Vorteilhaft ist jedoch, dass ein wesentlich breiteres Spektrum an Analysemethoden eingesetzt werden kann und Analysemethoden zur Anwendung kommen können, die entweder empflindlicher sind oder in anderer Weise mehr Informationen liefern als die für die berührungsfreie Beobachtung des Reaktionsgemisches anwendbaren Analysemethoden. So können die entnommenen Aliqote auch komplexerer qualitativer Analytik unterzogen werden, etwa indem deren Komponenten vor der eigentlichen analytischen Untersuchung mittels Gaschromatographie oder Hochleistungsflüssigkeitschromatographie aufgetrennt werden. Unter Umständen muss die Reaktion in den entnommenen Aliquoten verlangsamt oder zum Stillstand gebracht werden, um eine Verfälschung der Analyseergebnisse durch ein Fortlaufen der Reaktion nach der Probenentnahme zu unterbinden. Dies kann geschehen, indem man die entnommene Reaktionsmischung stark kühlt oder indem eine reaktive Komponente aus der Reaktionsmischung entfernt wird, beispielsweise durch Fällung.

Zur Messung von Konzentrations-Zeit-Profilen muss eine ausreichende Durchmischung der Reaktanten so schnell erfolgen, dass ein definierter Startzeitpunkt für die zu untersuchende Reaktion identifizierbar ist. Dies kann durch Miniaturisierung der verwendeten Versuchsaufbauten mittels des Einsatzes von Mikroreaktionstechnik erreicht werden, da dann die Transportwege für die Reaktanten verkürzt werden. Bei langsamen Reaktionen lassen sich definierte Stoffmengen unter Verwendung von einfachen Rührern, Strömungsrohren oder hochpräzisen Mischkammern vermischen. Bei schnelleren Reaktionen, die durch Zeitskalen im Minuten- bis Sekundenbereich charakterisiert sind, werden häufig spezielle Strömungsapparaturen verwendet. Bei extrem schnellen Reaktionen, die durch Zeitskalen im Millisekundenbereich charakterisiert sind, werden für schnelle und effiziente Mischung der Ausgangsstoffe optimierte Verfahren, wie etwa die Stopped-Flow-Methode, eingesetzt.

Eine zweite Gruppe von Verfahren zur Untersuchung extrem schneller Reaktionen mit charakteristischen Zeitskalen bis hinab zum Pikosekundenbereich sind Relaxationsverfahren. Diese beruhen auf dem Prinzip, die Ausgangsstoffe bereits deutlich vor dem eigentlichen Beobachtungszeitraum zu vermischen. Das Reaktionsgemisch beginnt zu reagieren. Nachdem sich in der Reaktionsmischung ein Gleichgewichtszustand eingestellt hat, wird dieser durch einen schnell applizierten Schock gestört und die Relaxation des Reaktionsgemisches in einen neuen Gleichgewichtszustand mit geeigneten Analysemethoden verfolgt. Beispiele für Relaxationsverfahren sind die Blitzlichtphotolyse sowie Temperatur-, Druck- und Feldsprungverfahren.

Erste qualitative Untersuchungen zur Kinetik wurden bereits um 1777 von Carl Friedrich Wenzel in seinem in Dresden erschienenen Werk Lehre von der Verwandtschaft der Körper berichtet. Später beschäftigten sich auch Claude-Louis Berthollet und William Higgins mit kinetischen Fragestellungen.^[20] Die erste wirklich grundlegende Arbeit zur Kinetik, die Spaltung von Rohrzucker unter Säureeinfluss, wurde von Ludwig Ferdinand Wilhelmy im Jahr 1850 vorgelegt.^[21] Jacobus Henricus van't Hoff untersuchte im Jahr 1896 die Verseifung von Essigester und die Hydrolyse von Chloressigsäure. Mathematisch formulierte er die Geschwindigkeitsgleichungen der Reaktionen. Ferner entwickelte er die grundlegenden Gesetze zu Temperaturabhängigkeit der Reaktionsgeschwindigkeit.^[22] Svante Arrhenius verbesserte die Ableitung und gab als Faustformel für die Änderung der Reaktionsgeschwindigkeit bei Temperaturerhöhung um 1 K eine Erhöhung der Reaktionsgeschwindigkeit um ca. 12 % an (siehe RGT-Regel). F. E. C. Scheffer und W. F. Brandsma führten im Jahr 1926 die Standard-Gibbs-Aktivierungsenergie für die Geschwindigkeitskonstante ein.^[23] Für die Entwicklung der Relaxationsverfahren zur Untersuchung der Kinetik schneller Reaktionen erhielten Manfred Eigen, Ronald Norrish und George Porter 1967 den Nobelpreis für Chemie.

• siehe Literatur zur Physikalischen Chemie

• Margaret Robson Wright: An Introduction to Chemical Kinetics. John Wiley & Sons, Chichester, UK 2004, ISBN 0-470-09060-X, doi:10.1002/047009060x.ch1. 
• Bernd Ralle, Ingo Eilks, Alfred Flint, Hartwig Möllencamp, Helmut Wenck: Handbuch der experimentellen Chemie: Sekundarbereich II. 8, Kinetik, Katalyse, Gleichgewicht. Hrsg.: Bernd Ralle, Ingo Eilks, Wolfgang Glöckner, Walter Jansen, Rudolf G. Weissenhorn. Aulis-Verlag Deubner, Köln 2004, ISBN 3-7614-2384-5. 
• Carl Heinz Hamann, Dirk Hoogestraat, Rainer Koch: Grundlagen der Kinetik: Von Transportprozessen zur Reaktionskinetik. Springer-Verlag, Berlin 2017, ISBN 978-3-662-49393-9, doi:10.1007/978-3-662-49393-9. 
• M. Dieter Lechner: Einführung in die Kinetik: Chemische Reaktionskinetik und Transporteigenschaften. Springer-Verlag, Berlin/ Heidelberg 2018, ISBN 978-3-662-57454-6, doi:10.1007/978-3-662-57455-3_1. 
• Hans-Dieter Bockhardt, Peter Güntzschel, Armin Poetschukat: „Grundlagen der Verfahrenstechnik für Ingenieure“ (mit dem Kapitel „Stoffumwandlung in Reaktoren“ S. 376–407 mit vielen spezifischen Unterkapiteln und einigen Beispielrechnungen), VEB Deutscher Verlag für Grundstoffindustrie, DDR, Leipzig, 1. Auflage 1981, Neuauflage ISBN 978-3-342-00684-8. (dieser erste Band ist das Lehrbuch), sowie von den gleichen Autoren und gleichem Verlag: „Aufgabensammlung zur Verfahrenstechnik für Ingenieure“, mit Kapitel „Stoffumwandlung in Reaktoren“ S. 193–210, (zum ersten Band gehöriges Übungsbuch mit vielen Aufgaben/Berechnungen und deren Lösungsweg und Lösungen, sowie den grundlegenden Definitionen, u. a. Bestimmung von Aktivierungsenergie, Reaktionsgeschwindigkeitskonstante und Reaktionsordnung), Deutscher Verlag für Grundstoffindustrie, 4. Auflage, Stuttgart 1998, ISBN 3-342-00683-8.

• G. J. Lauth: Einführung in die Reaktionskinetik. Vorlesungsreihe, Videoaufzeichnungen, 2013.

1. ↑ ^{a b c d e} K. J. Laidler: A glossary of terms used in chemical kinetics, including reaction dynamics (IUPAC Recommendations 1996). In: Pure and Applied Chemistry. Band 68, Nr. 1, 1996, ISSN 1365-3075, S. 181 f., doi:10.1351/pac199668010149. 
2. ↑ E.R. Cohen, T. Cvitas, J.G Frey, B. Holmstrom, K. Kuchitsu, R. Marquardt, I. Mills, F. Pavese, M. Quack, J. Stohner, H. Strauss, M. Takami, A.J. Thor: Quantities, Units and Symbols in Physical Chemistry (The Green Book). Hrsg.: International Union of Pure and Applied Chemistry. 3. Auflage. RSC Publishing, 2007, ISBN 978-1-84755-788-9, S. 63, doi:10.1039/9781847557889 (iupac.org [PDF; abgerufen am 19. April 2024]). 
3. ↑ Eintrag zu rate of reaction. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.R05156 – Version: 2.3.3.
4. ↑ DIN 13345-1978-08 Thermodynamik und Kinetik chemischer Reaktionen: Formelzeichen, Einheiten.
5. ↑ ^{a b c} Hans-Dieter Bockhardt, Peter Güntzschel, Armin Poetschukat: Aufgabensammlung zur Verfahrenstechnik für Ingenieure. 4. Auflage. Deutscher Verlag für Grundstoffindustrie, Stuttgart 1998, ISBN 3-342-00271-9, S. 195, Nr.(15.13). 
6. ↑ ^{a b} Hans-Dieter Bockhardt/Peter Güntzschel/Armin Poetschukat: Grundlagen der Verfahrenstechnik für Ingenieure, Deutscher Verlag für Grundstoffindustrie Leipzig 1981, 1. Auflage, S.391, ISBN (Neuauflage) 978-3342006848
7. ↑ Autorenkollektiv (K. Budde als federführender Autor): Reaktionstechnik III (Reihe Verfahrenstechnik), VEB Deutscher Verlag für Grundstoffindustrie, Leipzig, DDR, 1977, "Koeffizient für Volumenänderung durch Reaktion" S.9 u. 57
8. ↑ Autorenkollektiv (u. a. K. Budde als federführender Autor): Reaktionstechnik II (Reihe Verfahrenstechnik), VEB Deutscher Verlag für Grundstoffindustrie Leipzig, DDR, 1976, Koeffizient der Volumenänderung durch Reaktion S.11 u. 23
9. ↑ Extrembeispiel Luftchemie: Barbara Ervens et al.: Opinion: Challenges and needs of tropospheric chemical mechanism development. EGUsphere 2024 (Preprint), doi:10.5194/egusphere-2024-1316 (freier Volltext).
10. ↑ Grundlagen der ottomotorischen Verbrennung. Rwth-Aachen, abgerufen am 31. März 2024. 
11. ↑ OH + CH4 in der NIST Kinetics Database
12. ↑ Carl Heinz Hamann, Dirk Hoogestraat, Rainer Koch: Grundlagen der Kinetik: Von Transportprozessen zur Reaktionskinetik. Springer-Verlag, Berlin/ Heidelberg 2017, ISBN 978-3-662-49392-2, S. 116, doi:10.1007/978-3-662-49393-9. 
13. ↑ M. Dieter Lechner: Einführung in die Kinetik - Chemische Reaktionskinetik und Transporteigenschaften. Springer-Verlag, Berlin/ Heidelberg 2018, ISBN 978-3-662-57454-6, S. 13, doi:10.1007/978-3-662-57455-3_1. 
14. ↑ Christos Capellos, Benon H. J. Bielski: Kinetic systems: mathematical description of chemical kinetics in solution. Wiley-Interscience, 1972, ISBN 0-471-13450-3.
15. ↑ Robert G. Mortimer: Physical Chemistry. 2. Auflage. Academic Press, 2000, Kapitel 12 The Rates of Chemical Reactions. S. 408.
16. ↑ Ignacio Tinoco Jr., James C. Wang: Physical chemistry: principles and applications in biological sciences. 3. Auflage. Prentice Hall, 1995, ISBN 0-13-186545-5, S. 331.
17. ↑ Alisa Gapchenko: Styrol-Butylacrylat-Emulsion: Aspekte der Hochtemperatur-Copolymerisation und neue Anwendungsgebiete. Dissertation des Fachbereich Chemie der Fakultät für Mathematik, Informatik und Naturwissenschaften der Universität Hamburg 2018, abgerufen am 29. August 2020.
18. ↑ Lothar Papula: Übungen und Anwendung zur Mathematik für Chemiker. Enke Verlag, 1977, S. 382–385.
19. ↑ Klaus H. Homann: 13. Trimolekulare Reaktionen. In: Reaktionskinetik. Steinkopff-Verlag, Heidelberg 1975, S. 100–107, doi:10.1007/978-3-642-72314-8_13.
20. ↑ V. A. Kritsman: Ludwig Wilhelmy, Jacobus Henricus van't Hoff, Svante Arrhenius und die Geschichte der chemischen Kinetik. In: Chemie in unserer Zeit. Bd. 6, 1997, S. 291 ff.
21. ↑ L. Wilhelmy: Über das Gesetz, nach welchem die Einwirkung der Säuren auf den Rohrzucker stattfindet. In: Pogg. Ann. Band 81, 1850, S. 413–433, 499–526.
22. ↑ J. H. van't Hoff: Studien zur chemischen Dynamik. W. Engelmann, Leipzig 1896.
23. ↑ F. E. C. Scheffer, W. F. Brandsma: On reaction velocities. In: Recueil des Travaux Chimiques des Pays-Bas. Band 45, Nr. 7, 1926, S. 522–534, doi:10.1002/recl.19260450710.