Proof of Work
Unter einem Proof of Work (auch computational puzzle oder cryptographic puzzle; auf Deutsch etwa ‚Arbeitsnachweis‘ oder auch ‚-beweis‘, kurz PoW) versteht man in der Informatik eine Methode, die den übermäßigen Gebrauch eines Dienstes, wie beispielsweise Denial-of-Service-Attacken oder das massenweise Versenden von E-Mails (Spam), verhindern soll.
Der Proof-of-Work stellt in der Regel die Lösung einer mäßig schweren Aufgabe durch den Nutzer oder dessen Computer dar. Das Aufgabenergebnis kann vom Diensterbringer dagegen ohne großen Aufwand nachgeprüft werden.
Idee
Die Idee des Proof-of-Work ist, einen Dienstnutzer zuerst selbst etwas Arbeit verrichten zu lassen, bevor er den Dienst in Anspruch nehmen darf – eine Art Benutzungsentgelt. Sie wurde erstmals im Jahr 1992 von Cynthia Dwork und Moni Naor vorgeschlagen, um den Versand von Junk-Mails einzudämmen.[1][2] Eine Implementierung dieses Verfahrens ist beispielsweise Hashcash.
Der Proof-of-Work soll davon abhalten, einen Dienst übermäßig in Anspruch zu nehmen oder gar missbräuchlich zu verwenden. Es verzögert die Bearbeitung der Anfrage etwas, da der Dienstnutzer erst die Aufgabe lösen muss. Die Verzögerung sollte daher so gewählt werden, dass sie keine Störung im weiteren Ablauf darstellt. Zum Beispiel ist eine Verzögerung von wenigen Sekunden beim Versand einer E-Mail meist hinnehmbar, bremst aber deutlich die Anzahl der versendbaren E-Mails innerhalb eines Zeitintervalls aus. Das stört den durchschnittlichen E-Mail-Versender kaum, verhindert aber u. U. das Spamming.
Es existieren zahlreiche Probleme aus Bereichen wie der Kryptologie oder der Numerik, deren Lösung nur aufwendig zu berechnen ist, die anschließend aber leicht auf Korrektheit geprüft werden kann. Ideal sind Probleme, deren Lösungsaufwand man zusätzlich noch durch leichte Anpassung der Aufgabenstellung beeinflussen kann. So lässt sich der Aufwand, den der Nutzer erbringen muss, an die Gegebenheiten, beispielsweise die verfügbare Rechenleistung, anpassen.
Beispiele für solche Probleme sind u. a.
- das Lösen von Differentialgleichungen,
- Brute-Force-Angriffe auf abgeschwächte kryptographische Primitiven,
- Operationen auf großen, dicht besetzten Matrizen, wie das Lösen linearer Gleichungssysteme oder Invertieren.
Beispiel
Im Jahr 1999 schlugen Ari Juels und John Brainard, zwei Mitarbeiter der RSA Laboratories, folgende Aufgabe vor: Der Benutzer erhält den Hashwert einer Zeichenkette, sowie einen unvollständigen Teil der Zeichenkette. Er muss anhand des Hashwerts die fehlenden Zeichen bestimmen.[3][4]

Eine weitverbreitete Abwandlung dieses Verfahrens findet beispielsweise auch bei der Kryptowährung Bitcoin Anwendung: Zu einer gegebenen Zeichenkette muss ein Nonce gefunden werden, sodass im Hash über die Zeichenkette und den Nonce die ersten m Bits Nullen sind. Durch die Wahl der Anzahl m dieser Null-Bits lässt sich die Schwierigkeit und damit auch die Dauer der Berechnung steuern.
Protokolle und Problemklassen
Es gibt zwei Arten von Proof-of-Work-Protokollen:
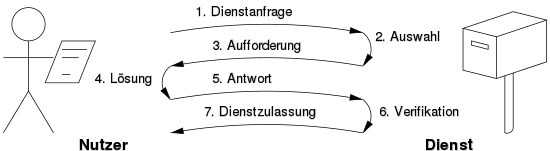
- Challenge-Response: Diese Variante benötigt eine direkte Verbindung zwischen dem Dienst und seinem Nutzer. Der Dienst sucht eine Herausforderung (Aufforderung), der Nutzer löst sie (mit Aufwand) und der Dienst kann sie leicht verifizieren. Da die Aufforderung spontan vom Dienst ausgewählt wird, kann er ihre Schwierigkeit an die aktuelle Auslastung anpassen. Der Aufwand kann auf Nutzerseite begrenzt sein, wenn das Aufforderung-Antwort-Protokoll eine (vom Dienst ausgewählte) bekannte Lösung hat oder wenn von ihr bekannt ist, sich in einem begrenzten Suchraum zu befinden.
- Lösungsverifikation: Bei dieser Variante wird keine direkte Verbindung benötigt. Daher muss das Problem selbsterklärend und omnipräsent sein. Der Dienst muss dann die Problemwahl und die errechnete Lösung verifizieren. Die meisten dieser Verfahren sind unbeschränkte, probabilistische, iterative Verfahren wie Hashcash.

Der in eine Lösung gesteckte Aufwand muss sich im Verbrauch materieller Ressourcen und Energie niederschlagen. Daher unterscheidet man folgende Klassen von Problemen:
- Rechenbasiert (compute bound): Es wird Energie und Zeit verbraucht. Je nach Rechenleistung kann eine Lösung einfacher berechnet werden.
- Speicherbasiert (memory bound): Die Lösung des Problems benötigt viel Speicher. Dadurch wird die Anzahl gleichzeitiger Anfragen limitiert. Je nach Größe spielen Speicherbandbreite und Latenz eine Rolle (Cache-misses)
- Netzwerkbasiert: Der Konsument muss für seine Berechnung viele oder schlecht erreichbare Netzknoten kontaktieren. Dadurch wird er zeitlich gebremst oder künstlich, indem die Anfragen künstlich limitiert werden.
Siehe auch
Literatur
- Xiao-Weng Fang: Encyclopedia of Cryptography and Security, Band 1: Computational Puzzles. 2. Auflage. Springer, 2011, ISBN 978-1-4419-5905-8, S. 244 f.
Einzelnachweise
- ↑ Pricing via Processing or Combatting Junk Mail. Abgerufen am 18. März 2014 (englisch).
- ↑ Pricing via Processing or Combatting Junk Mail. Abgerufen am 18. März 2014 (englisch).
- ↑ Proceedings of the 1999 Network and Distributed System Security Symposium. Abgerufen am 18. März 2014 (englisch).
- ↑ Client Puzzles: A Cryptographic Countermeasure Against Connection Depletion Attacks. Abgerufen am 18. März 2014 (englisch).
