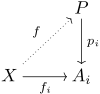Produkt von Moduln
In vielen Gebieten der Mathematik spielen direkte Produkte und Koprodukte der betrachteten Objekte eine besondere Rolle. Die Konstruktion solcher Produkte von Objektfamilien fußt oft auf dem kartesischen Produkt von Mengen.
In der Mengenlehre wird das kartesische Produkt einer Familie von Mengen folgendermaßen definiert:
Sind die alles Rechtsmoduln über dem unitären Ring , so hat eine Modulstruktur. Dies ist ein Produkt von Moduln, das Produkt der Modulfamilie .
Definition des Produktes
Produkt von Moduln
Ist eine Familie von Rechtsmoduln über dem Ring so heißt das Produkt der Moduln. Ist , so heißt die -te Komponente von . Das Produkt erhält durch die folgenden beiden Verknüpfungen eine Modulstruktur.
Ist die Funktion , so schreibt man dafür oft , analog wie das bei reellen Zahlenfolgen üblich ist[1]. Dabei ist die -te Komponente. Man addiert also komponentenweise und mit den Skalaren wird komponentenweise multipliziert.
Universelle Eigenschaft des Produktes
Ist das Produkt der Moduln so bilden die Funktionen das Produkt epimorph auf ab. Sie heißen Projektionen. Das Paar hat die folgende Eigenschaft:
Zu jedem Rechtsmodul über und jeder Familie von Homomorphismen gibt es genau einen Homomorphismus , so dass für alle gilt.
In der Kategorientheorie nennt man eine solche Eigenschaft universell, sie kennzeichnet das Produkt von Objekten bis auf Isomorphie, das heißt:
Ist ein Modul und eine Familie von Homomorphismen und gibt es zu jedem Modul und jeder Familie von Homomorphismen genau ein mit , so ist . Ein Diagramm zu dieser Situation sieht so aus:
Die oben angegebene Konstruktion zusammen mit dem Nachweis der universellen Eigenschaft fasst man auch kurz so zusammen: In der Kategorie der Moduln gibt es Produkte.
Produkt und Hom Funktor
Ist eine Familie von Homomorphismen, so ist genau dann ein Produkt der Familie , wenn der Homomorphismus
für alle Rechtsmoduln ein Isomorphismus ist. Insbesondere ist:
eine natürliche Transformation, die für jeden Modul ein Isomorphismus ist. ist ein funktorieller Isomorphismus.
Beispiele, Bemerkungen, Bezeichnungen
- Ist für alle , so schreibt man und nennt dies eine Potenz von .
- Für jede Indexmenge ist sogar ein Ring, wenn man komponentenweise multipliziert. ist auf der linken und rechten Seite ein Modul über dem Ring . Die Diagonalabbildung ist ein Homomorphismus der Ringe und der Moduln. Dabei sind alle Komponenten von gleich r.
- Ist eine Familie von Untermoduln, so gibt es einen eindeutig bestimmten Homomorphismus mit . Dabei ist die Familie der kanonischen Homomorphismen von auf die Faktormoduln . Der Kern dieses Homomorphismus ist .
- Sind und zwei Familien von Moduln und ist eine Familie von Homomorphismen, so ist die Abbildung ein Homomorphismus. Es ist . Weiter ist .
- Ist auch eine Familie von Moduln und ist für alle die Folge exakt, so ist exakt.
- Sind Rechtsmoduln, so gibt es einen eindeutig bestimmten Homomorphismus mit für alle . Es ist . Ist der Endomorphismenring von , so ist auf der linken Seite ein S– Untermodul von . Ist so koerzeugt der Modul den Modul . Ein Modul, der alle Rechtsmoduln koerzeugt heißt Kogenerator. Der Modul ist daher ein Kogenerator, wenn es zu jedem Rechtsmodul einen Monomorphismus gibt, für eine gewisse Indexmenge [2].
- Ist eine abelsche Gruppe, so ist torsionsfrei genau dann, wenn von koerzeugt wird.[3]
- ist ein Kogenerator in der Kategorie der abelschen Gruppen. Dies ist nicht mehr ganz einfach. Es setzt die Theorie der injektiven Moduln voraus. Siehe dazu zum Beispiel[4]
Koprodukt von Moduln
Eine Funktion heißt endlichwertig, wenn nur für endlich viele gilt. Man meint dasselbe, wenn man sagt für fast alle . Die Menge der endlichwertigen Abbildungen aus wird Koprodukt (oder äußere direkte Summe) der Familie genannt und mit bezeichnet. ist ein Untermodul des Produktes.
Ist , so sei die folgende Abbildung aus :
Schreibt man die Abbildung als Tupel, so ist . An allen Stellen des Tupels steht 0 nur an der j-ten Stelle steht a.
- ist der einzige Homomorphismus , welcher folgende Bedingung erfüllt:
Dies ergibt sich aus der universellen Eigenschaft des Produktes. Die sind alles Monomorphismen und es ist die direkte Summe der in dem Produkt der .
Universelle Eigenschaft des Koproduktes
Ist das Koprodukt der Moduln so bilden die Funktionen
die monomorph nach ab. Sie heißen Injektionen. Das Paar hat die folgende Eigenschaft:
Zu jedem Modul und jeder Familie von Homomorphismen gibt es genau einen Homomorphismus , so dass für alle gilt.
In der Kategorientheorie kennzeichnet diese universelle Eigenschaft das Koprodukt von Objekten bis auf Isomorphie, das heißt:
Ist ein Modul und eine Familie von Homomorphismen und gibt es zu jedem Modul und jeder Familie von Homomorphismen genau ein mit , so ist .
Die oben angegebene Konstruktion zusammen mit dem Nachweis der universellen Eigenschaft fasst man auch kurz so zusammen: In der Kategorie der Moduln gibt es Koprodukte.
Koprodukt und Hom Funktor
Ist eine Familie von Homomorphismen, so ist genau dann ein Koprodukt der Familie , wenn der Homomorphismus
für alle Rechtsmoduln ein Isomorphismus ist. Insbesondere ist:
ein funktorieller Isomorphismus.
Bezeichnungen und Beispiele
- Meist identifiziert man die mit den in . Dann schreibt man anstelle von . Normalerweise ist keine Verwechslung zu befürchten.
- Ist für alle so schreibt man anstelle von .
- Ist für alle , so ist ein freier Modul. Eine Basis ist die Familie mit .
- Ist die Indexmenge endlich, so sind direkte Summe und direktes Produkt identisch.
- Ist eine endliche Teilmenge von und , so ist direkter Summand in . Der Homomorphismus erfüllt die Bedingungen und . Für unendliche Mengen ist die direkte Summe normalerweise keineswegs direkter Summand im direkten Produkt. So ist kein direkter Summand in . Eine schwierige Frage ist: Für welche Moduln ist direkter Summand im Produkt ? Ist beispielsweise halbeinfach und endlich erzeugt, so ist dies der Fall.
- Sind Rechtsmoduln, so gibt es einen eindeutig bestimmten Homomorphismus mit für alle . Es ist . Ist der Endomorphismenring von , so ist auf der linken Seite ein S– Untermodul von . Ist , so erzeugt der Modul den Modul . Ein Modul, der alle Rechtsmoduln erzeugt heißt Generator. Der Modul ist daher ein Generator, wenn es zu jedem Rechtsmodul einen Epimorphismus gibt, für eine gewisse Indexmenge . Da jeder Modul das epimorphe Bild eines freien Moduls ist, ist ein Generator.
Zwei wichtige Sätze
Ein Zerlegungssatz Satz von Kaplansky
Sei eine unendliche Kardinalzahl. Ist der Modul direkte Summe von erzeugbaren Untermoduln, so ist jeder direkte Summand von direkte Summe von erzeugbaren Untermoduln.
Der wichtigste Fall ist: Ist direkte Summe von abzählbar erzeugten Untermoduln, so hat jeder direkte Summand diese Eigenschaft. In dieser Form hat Irving Kaplansky den Satz ursprünglich bewiesen. Daraus folgt beispielsweise, dass jeder projektive Modul direkte Summe von abzählbar erzeugten Moduln ist. Will man daher Struktursätze über projektive Moduln beweisen, so kann man sich dank Kaplansky auf abzählbar erzeugte beschränken. Jeder projektive Modul ist ja direkter Summand in einem freien Modul.
Der Zerlegungssatz von Krull-Remak-Schmidt-Azmaya
Seien zwei Zerlegungen von . Sind die Endomorphismenringe aller lokal und sind alle unzerlegbar, so gibt es eine Bijektion mit für alle .
Dieser Satz verallgemeinert viele wichtige Sätze. So zum Beispiel:
- Je zwei Basen eines Vektorraumes haben gleiche Mächtigkeit.
- Die Zerlegung eines halbeinfachen Moduls in eine direkte Summe von einfachen Moduln ist im Sinne des Satzes eindeutig.
- Der Zerlegungssatz von Satz von Krull-Remak-Schmidt für Moduln endlicher Länge.
Einzelnachweise
- ↑ Friedrich Kasch Moduln und Ringe. Teubner, Stuttgart 1977, Seite 77 ISBN 3-519-02211-7
- ↑ Robert Wisbauer, Grundlagen der Modul – und Ringtheorie, Verlag Reinhard Fischer, München 1988 Seite 112 ISBN 3-88927-044-1
- ↑ Frank W. Anderson, Kent R. Fuller, Rings and Categories of modules Springe, New York Berlin Heidelberg, 1992, Seite 106, ISBN 0-387-97845-3
- ↑ Friedrich Kasch Moduln und Ringe. Teubner, Stuttgart 1977, Seite 127 ISBN 3-519-02211-7
Literatur
- Frank W. Anderson and Kent R. Fuller: Rings and Categories of Modules. Springer, New-York 1992, ISBN 0-387-97845-3
- Friedrich Kasch: Moduln und Ringe. Teubner, Stuttgart 1977, ISBN 3-519-02211-7
- Robert Wisbauer: Grundlagen der Modul- und Ringtheorie. Reinhard Fischer, München 1988, ISBN 3-88927-044-1