Die lokale Struktur ist ein Begriff aus der nuklearen Festkörperspektroskopie, der die nahe Umgebung eines Atoms mit seinen benachbarten Atomen in Kristallen und Molekülen beschreibt.

Die Atome in Kristallen bilden beispielsweise sehr weit ausgedehnte regelmäßige Strukturen, deren Ordnung auch im makroskopischen Maßstab erhalten bleibt, siehe Naica-Höhle. Jedoch ist die Gitterstruktur von Kristallen nicht perfekt, sondern enthält Defekte. Das sind Fehlstellen, an denen ein Element eines Gitterplatzes durch ein anderes Element ersetzt ist (Substitution) oder ein Atom (fremd im Kristall oder nicht) auf einem Zwischengitterplatz sitzt. Ferner sind noch Leerstellen möglich, an denen ein Atom fehlt; sie haben große Bedeutung für die Diffusion in Kristallgittern.

Mit den Methoden der nuklearen Festkörperspektroskopie ist es möglich, den Atomkern als Sonde zu verwenden und die Hyperfeinwechselwirkung des Atomkerns mit den ihn umgebenden lokalen elektrischen und magnetischen Feldern zu messen.

Der Atomkern ist ca. 10.000–150.000 mal kleiner als das Atom, so dass er als nahezu punktförmig betrachtet werden kann.

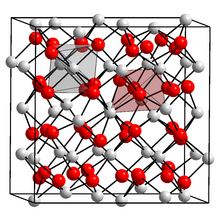
Die elektrischen Felder entstehen durch die Elektronen der Atomhülle und sind beeinflusst durch die nächsten Nachbaratome. Im obigen Beispiel von NaCl ist jedes Natriumatom (genauer Natriumion) von 6 Chloratomen umgeben, die ein Oktaeder um das Natriumatom bilden, siehe blau gefärbtes Objekt. Wenn alle Ladungen sich symmetrisch um das Natriumatom verteilen, was in kubischen Kristallgittern meist der Fall ist, heben sie sich am Kernort auf.

Ist das nicht der Fall, so erfährt der Kern ein sich graduell änderndes Feld, siehe elektrischer Feldgradient (EFG).^[1] Die Größenordnung des EFG beträgt etwa 10²¹ V/m². Besonders groß können die Felder bei Defekten sein. Methoden der nuklearen Festkörperspektroskopie wie die Mößbauer-Spektroskopie oder die Gestörte Gamma-Gamma-Winkelkorrelation ermöglichen die direkte Messung der statistischen Verteilung des EFG in einer Struktur. In Verbindung mit Berechnungen des EFG mit der Dichtefunktionaltheorie können verbesserte Modelle der lokalen Struktur erstellt werden.

Bei magnetischen Materialien zeichnet sich das gleiche Bild ab wie gerade beschrieben, nur dass hier lokale Magnetfelder betrachtet werden.

Das Verständnis der lokalen Struktur spielt in funktionellen Materialien eine Rolle, die häufig durch ihre Defektchemie bestimmt werden. Anwendungen finden sich in keramischen elektronischen Bauteilen, Halbleitermaterialien, Computerchips, Batterien, Solarzellen oder den vielen magnetischen Materialien, die z. B. bei Festplatten oder in Magneten angewendet werden.

1. ↑ Kaufmann, Elton N; Reiner J. Vianden (1979). "The electric field gradient in noncubic metals". Reviews of Modern Physics. 51 (1): 161–214. doi:10.1103/RevModPhys.51.161.