Liste kleiner Gruppen

Die folgende Liste enthält eine Auswahl endlicher Gruppen kleiner Ordnung.

Diese Liste kann benutzt werden, um herauszufinden, zu welchen bekannten endlichen Gruppen eine Gruppe G isomorph ist. Als erstes bestimmt man die Ordnung von G und vergleicht sie mit den unten aufgelisteten Gruppen gleicher Ordnung. Ist bekannt, ob G abelsch (kommutativ) ist, so kann man einige Gruppen ausschließen. Anschließend vergleicht man die Ordnung einzelner Elemente von G mit den Elementen der aufgelisteten Gruppen, wodurch man G bis auf Isomorphie eindeutig bestimmen kann.

Glossar

In der nachfolgenden Liste werden folgende Bezeichnungen verwendet:

$\mathbb {Z} _{n}$ ist die zyklische Gruppe der Ordnung $n$ (die auch als $C_{n}$ oder $\mathbb {Z} /n\mathbb {Z}$ geschrieben wird).
$D_{n}$ ist die Diedergruppe der Ordnung $2n$ .
$S_{n}$ ist die symmetrische Gruppe vom Grad $n$ , mit n! Permutationen von $n$ Elementen.
$A_{n}$ ist die alternierende Gruppe vom Grad $n$ , mit $n!/2$ Permutationen von $n$ Elementen für $n\geq 2$ .
$\mathrm {Dic} _{n}$ ist die dizyklische Gruppe der Ordnung $4n$ .
$V_{4}$ ist die Klein’sche Vierergruppe der Ordnung $4$ .
$Q_{4n}$ ist die Quaternionengruppe der Ordnung $4n$ für $n\geq 2$ .

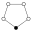
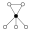
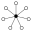
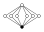
Die Notation $G\times H$ wird benutzt, um das direkte Produkt der Gruppen $G$ und $H$ zu bezeichnen. Es wird angemerkt, ob eine Gruppe abelsch oder einfach ist. (Für Gruppen der Ordnung $n<60$ sind die einfachen Gruppen genau die zyklischen Gruppen $\mathbb {Z} _{n}$ , mit $n$ aus der Menge der Primzahlen.) In den Zykel-Graphen der Gruppen wird das neutrale Element durch einen ausgefüllten schwarzen Kreis dargestellt. Ordnung $16$ ist die kleinste Ordnung, für welche die Gruppenstruktur durch den Zykel-Graphen nicht eindeutig bestimmt ist: Die nichtabelsche modulare Gruppe und $\mathbb {Z} _{8}\times \mathbb {Z} _{2}$ haben den gleichen Zykel-Graphen und den gleichen (modularen) Untergruppenverband, sind aber nicht isomorph.

Es ist zu beachten, dass $3\cdot \mathbb {Z} _{2}$ bedeutet, dass es 3 Untergruppen vom Typ $\mathbb {Z} _{2}$ gibt (nicht die Nebenklasse von $\mathbb {Z} _{2}$ ).

Zu jeder Ordnung wird zunächst die zyklische Gruppe angegeben, dann folgen gegebenenfalls weitere abelsche Gruppen und dann gegebenenfalls nichtabelsche Gruppen:

Liste aller Gruppen bis Ordnung 24

Ordnung	Gruppe	Echte Untergruppen^[1]	Eigenschaften
1	$\mathbb {Z} _{1}\cong S_{1}\cong A_{2}$ (triviale Gruppe)	-	abelsch, zyklisch
2	$\mathbb {Z} _{2}\cong S_{2}\cong D_{1}$ (Gruppe Z₂)	-	abelsch, einfach, zyklisch, kleinste nichttriviale Gruppe
3	$\mathbb {Z} _{3}\cong A_{3}$	-	abelsch, einfach, zyklisch
4	$\mathbb {Z} _{4}\cong \mathrm {Dic} _{1}$	$\mathbb {Z} _{2}$	abelsch, zyklisch
4	$V_{4}\cong \mathbb {Z} _{2}^{2}\cong D_{2}$ (Kleinsche Vierergruppe)	$3\cdot \mathbb {Z} _{2}$	abelsch, die kleinste nichtzyklische Gruppe
5	$\mathbb {Z} _{5}$	-	abelsch, einfach, zyklisch
6	$\mathbb {Z} _{6}\cong \mathbb {Z} _{2}\times \mathbb {Z} _{3}$	$\mathbb {Z} _{3}$ , $\mathbb {Z} _{2}$	abelsch, zyklisch
6	$S_{3}\cong D_{3}$ (Symmetrische Gruppe)	$\mathbb {Z} _{3}$ , $3\cdot \mathbb {Z} _{2}$	kleinste nichtabelsche Gruppe
7	$\mathbb {Z} _{7}$	-	abelsch, einfach, zyklisch
8	$\mathbb {Z} _{8}$	$\mathbb {Z} _{4}$ , $\mathbb {Z} _{2}$	abelsch, zyklisch
	$\mathbb {Z} _{2}\times \mathbb {Z} _{4}$	$2\cdot \mathbb {Z} _{4}$ , $3\cdot \mathbb {Z} _{2}$ , $D_{2}$	abelsch
	$\mathbb {Z} _{2}^{3}\cong D_{2}\times \mathbb {Z} _{2}$	$7\cdot \mathbb {Z} _{2}$ , $7\cdot D_{2}$	abelsch
	$D_{4}$	$\mathbb {Z} _{4}$ , $2\cdot D_{2}$ , $5\cdot \mathbb {Z} _{2}$	nichtabelsch
	$Q_{8}\cong \mathrm {Dic} _{2}$ (Quaternionengruppe)	$3\cdot \mathbb {Z} _{4}$ , $\mathbb {Z} _{2}$	nichtabelsch; die kleinste hamiltonsche Gruppe
9	$\mathbb {Z} _{9}$	$\mathbb {Z} _{3}$	abelsch, zyklisch
9	$\mathbb {Z} _{3}^{2}$	$4\cdot \mathbb {Z} _{3}$	abelsch
10	$\mathbb {Z} _{10}\cong \mathbb {Z} _{2}\times \mathbb {Z} _{5}$	$\mathbb {Z} _{5}$ , $\mathbb {Z} _{2}$	abelsch, zyklisch
10	$D_{5}$	$\mathbb {Z} _{5}$ , $5\cdot \mathbb {Z} _{2}$	nichtabelsch
11	$\mathbb {Z} _{11}$	-	abelsch, einfach, zyklisch
12	$\mathbb {Z} _{12}\cong \mathbb {Z} _{4}\times \mathbb {Z} _{3}$	$\mathbb {Z} _{6}$ , $\mathbb {Z} _{4}$ , $\mathbb {Z} _{3}$ , $\mathbb {Z} _{2}$	abelsch, zyklisch
	$\mathbb {Z} _{2}\times \mathbb {Z} _{6}\cong \mathbb {Z} _{2}^{2}\times \mathbb {Z} _{3}\cong D_{2}\times \mathbb {Z} _{3}$	$3\cdot \mathbb {Z} _{6}$ , $\mathbb {Z} _{3}$ , $D_{2}$ , $3\cdot \mathbb {Z} _{2}$	abelsch
	$D_{6}\cong D_{3}\times \mathbb {Z} _{2}$	$\mathbb {Z} _{6}$ , $2\cdot D_{3}$ , $3\cdot D_{2}$ , $\mathbb {Z} _{3}$ , $7\cdot \mathbb {Z} _{2}$	nichtabelsch
	$A_{4}$ (Gruppe A₄)	$D_{2}$ , $4\cdot \mathbb {Z} _{3}$ , $3\cdot \mathbb {Z} _{2}$	nichtabelsch; kleinste Gruppe, die zeigt, dass die Umkehrung des Satzes von Lagrange nicht stimmt: keine Untergruppe der Ordnung 6
	$\mathrm {Dic} _{3}$ (hier Verknüpfungstafel)	$\mathbb {Z} _{6}$ , $3\cdot \mathbb {Z} _{4}$ , $\mathbb {Z} _{3}$ , $\mathbb {Z} _{2}$	nichtabelsch
13	$\mathbb {Z} _{13}$	-	abelsch, einfach, zyklisch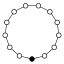
14	$\mathbb {Z} _{14}\cong \mathbb {Z} _{2}\times \mathbb {Z} _{7}$	$\mathbb {Z} _{7}$ , $\mathbb {Z} _{2}$	abelsch, zyklisch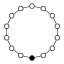
14	$D_{7}$	$\mathbb {Z} _{7}$ , $7\cdot \mathbb {Z} _{2}$	nichtabelsch
15	$\mathbb {Z} _{15}\cong \mathbb {Z} _{3}\times \mathbb {Z} _{5}$	$\mathbb {Z} _{5}$ , $\mathbb {Z} _{3}$	abelsch, zyklisch (siehe „Jede Gruppe der Ordnung 15 ist zyklisch.“)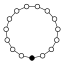
16	$\mathbb {Z} _{16}$	$\mathbb {Z} _{8}$ , $\mathbb {Z} _{4}$ , $\mathbb {Z} _{2}$	abelsch, zyklisch
	$\mathbb {Z} _{2}^{4}$	$15\cdot \mathbb {Z} _{2}$ , $35\cdot D_{2}$ , $15\cdot \mathbb {Z} _{2}^{3}$	abelsch
	$\mathbb {Z} _{4}\times \mathbb {Z} _{2}^{2}$	$7\cdot \mathbb {Z} _{2}$ , $4\cdot \mathbb {Z} _{4}$ , $7\cdot D_{2}$ , $\mathbb {Z} _{2}^{3}$ , $6\cdot \mathbb {Z} _{4}\times \mathbb {Z} _{2}$	abelsch
	$\mathbb {Z} _{8}\times \mathbb {Z} _{2}$	$3\cdot \mathbb {Z} _{2}$ , $2\cdot \mathbb {Z} _{4}$ , $D_{2}$ , $2\cdot \mathbb {Z} _{8}$ , $\mathbb {Z} _{4}\times \mathbb {Z} _{2}$	abelsch
	$\mathbb {Z} _{4}^{2}$	$3\cdot \mathbb {Z} _{2}$ , $6\cdot \mathbb {Z} _{4}$ , $D_{2}$ , $3\cdot \mathbb {Z} _{4}\times \mathbb {Z} _{2}$	abelsch
	$D_{8}$	$\mathbb {Z} _{8}$ , $2\cdot D_{4}$ , $4\cdot D_{2}$ , $\mathbb {Z} _{4}$ , $9\cdot \mathbb {Z} _{2}$	nichtabelsch
	$D_{4}\times \mathbb {Z} _{2}$	$4\cdot D_{4}$ , $\mathbb {Z} _{4}\times \mathbb {Z} _{2}$ , $2\cdot \mathbb {Z} _{2}^{3}$ , $13\cdot \mathbb {Z} _{2}^{2}$ , $2\cdot \mathbb {Z} _{4}$ , $11\cdot \mathbb {Z} _{2}$	nichtabelsch
	$Q_{16}\cong \mathrm {Dic_{4}}$	$\mathbb {Z} _{8}$ , $2\cdot Q_{8}$ , $5\cdot \mathbb {Z} _{4}$ , $\mathbb {Z} _{2}$	nichtabelsch
	$Q_{8}\times \mathbb {Z} _{2}$	$3\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{4}$ , $4\cdot Q_{8}$ , $6\cdot \mathbb {Z} _{4}$ , $\mathbb {Z} _{2}\times \mathbb {Z} _{2}$ , $3\cdot \mathbb {Z} _{2}$	nichtabelsch, hamiltonsche Gruppe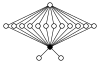
	Quasi-Diedergruppe	$\mathbb {Z} _{8}$ , $Q_{8}$ , $D_{4}$ , $3\cdot \mathbb {Z} _{4}$ , $2\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{2}$ , $5\cdot \mathbb {Z} _{2}$	nichtabelsch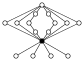
	Nichtabelsche nicht-hamiltonsche modulare Gruppe	$2\cdot \mathbb {Z} _{8}$ , $\mathbb {Z} _{4}\times \mathbb {Z} _{2}$ , $2\cdot \mathbb {Z} _{4}$ , $\mathbb {Z} _{2}\times \mathbb {Z} _{2}$ , $3\cdot \mathbb {Z} _{2}$	nichtabelsch
	Semidirektes Produkt $\mathbb {Z} _{4}\rtimes \mathbb {Z} _{4}$ (siehe hier)	$3\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{4}$ , $6\cdot \mathbb {Z} _{4}$ , $\mathbb {Z} _{2}\times \mathbb {Z} _{2}$ , $3\cdot \mathbb {Z} _{2}$	nichtabelsch
	Die durch Pauli-Matrizen erzeugte Gruppe.	$3\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{4}$ , $3\cdot D_{4}$ , $Q_{8}$ , $4\cdot \mathbb {Z} _{4}$ , $3\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{2}$ , $7\cdot \mathbb {Z} _{2}$	nichtabelsch
	$G_{4,4}=V_{4}\rtimes \mathbb {Z} _{4}$	$2\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{4}$ , $\mathbb {Z} _{2}\times \mathbb {Z} _{2}\times \mathbb {Z} _{2}$ , $4\cdot \mathbb {Z} _{4}$ , $7\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{2}$ , $7\cdot \mathbb {Z} _{2}$	nichtabelsch
17	$\mathbb {Z} _{17}$	-	abelsch, einfach, zyklisch
18	$\mathbb {Z} _{18}\cong \mathbb {Z} _{9}\times \mathbb {Z} _{2}$	$\mathbb {Z} _{9},$ $\mathbb {Z} _{6},$ $\mathbb {Z} _{3},$ $\mathbb {Z} _{2}$	abelsch, zyklisch
	$\mathbb {Z} _{6}\times \mathbb {Z} _{3}$	$\mathbb {Z} _{3}^{2},$ $4\cdot \mathbb {Z} _{6},$ $4\cdot \mathbb {Z} _{3},$ $\mathbb {Z} _{2}$	abelsch
	$D_{9}$	$\mathbb {Z} _{9},$ $3\cdot D_{3},$ $\mathbb {Z} _{3},$ $9\cdot \mathbb {Z} _{2}$	nichtabelsch
	$S_{3}\times \mathbb {Z} _{3}$	$\mathbb {Z} _{3}^{2},$ $D_{3},$ $3\cdot \mathbb {Z} _{6},$ $4\cdot \mathbb {Z} _{3},$ $3\cdot \mathbb {Z} _{2}$	nichtabelsch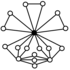
	$(\mathbb {Z} _{3}\times \mathbb {Z} _{3})\rtimes _{\alpha }\mathbb {Z} _{2}$ mit $\alpha (1)={\begin{pmatrix}2&0\\0&2\end{pmatrix}}$	$\mathbb {Z} _{3}^{2},$ $12\cdot D_{3},$ $4\cdot \mathbb {Z} _{3},$ $9\cdot \mathbb {Z} _{2}$	nichtabelsch
19	$\mathbb {Z} _{19}$	-	abelsch, einfach, zyklisch
20	$\mathbb {Z} _{20}\cong \mathbb {Z} _{5}\times \mathbb {Z} _{4}$	$\mathbb {Z} _{10},$ $\mathbb {Z} _{5},$ $\mathbb {Z} _{4},$ $\mathbb {Z} _{2}$	abelsch, zyklisch
	$\mathbb {Z} _{10}\times \mathbb {Z} _{2}\cong \mathbb {Z} _{5}\times \mathbb {Z} _{2}\times \mathbb {Z} _{2}$	$3\cdot \mathbb {Z} _{10},$ $\mathbb {Z} _{5},$ $D_{2},$ $3\cdot \mathbb {Z} _{2}$	abelsch
	$Q_{20}\cong \mathrm {Dic} _{5}$	$\mathbb {Z} _{10},$ $\mathbb {Z} _{5},$ $5\cdot \mathbb {Z} _{4},$ $\mathbb {Z} _{2}$	nichtabelsch
	$\mathbb {Z} _{5}\rtimes \mathbb {Z} _{4}\cong$ AGL₁(5)	$D_{5},$ $\mathbb {Z} _{5},$ $5\cdot \mathbb {Z} _{4},$ $5\cdot \mathbb {Z} _{2}$	nichtabelsch
	$D_{10}\cong D_{5}\times \mathbb {Z} _{2}$	$\mathbb {Z} _{10},$ $D_{5},$ $\mathbb {Z} _{5},$ $5\cdot V_{4},$ $11\cdot \mathbb {Z} _{2}$	nichtabelsch
21	$\mathbb {Z} _{21}\cong \mathbb {Z} _{7}\times \mathbb {Z} _{3}$	$\mathbb {Z} _{7},$ $\mathbb {Z} _{3}$	abelsch, zyklisch
21	$\mathbb {Z} _{7}\rtimes \mathbb {Z} _{3}$	$\mathbb {Z} _{7},$ $7\cdot \mathbb {Z} _{3}$	nichtabelsch
22	$\mathbb {Z} _{22}\cong \mathbb {Z} _{11}\times \mathbb {Z} _{2}$	$\mathbb {Z} _{11},$ $\mathbb {Z} _{2}$	abelsch, zyklisch
22	$D_{11}$	$\mathbb {Z} _{11},$ $11\cdot \mathbb {Z} _{2}$	nichtabelsch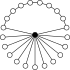
23	$\mathbb {Z} _{23}$	-	abelsch, einfach, zyklisch
24	$\mathbb {Z} _{24}\cong \mathbb {Z} _{8}\times \mathbb {Z} _{3}$	$\mathbb {Z} _{12},$ $\mathbb {Z} _{8},$ $\mathbb {Z} _{6},$ $\mathbb {Z} _{4},$ $\mathbb {Z} _{3},$ $\mathbb {Z} _{2}$	abelsch, zyklisch
	$\mathbb {Z} _{12}\times \mathbb {Z} _{2}\cong \mathbb {Z} _{6}\times \mathbb {Z} _{4}\cong$ $\mathbb {Z} _{4}\times \mathbb {Z} _{3}\times \mathbb {Z} _{2}$	$\mathbb {Z} _{12},$ $\mathbb {Z} _{6},$ $\mathbb {Z} _{4},$ $\mathbb {Z} _{3},$ $\mathbb {Z} _{2}$	abelsch
	$\mathbb {Z} _{6}\times D_{2}\cong \mathbb {Z} _{3}\times \mathbb {Z} _{2}^{3}$	$\mathbb {Z} _{6},$ $\mathbb {Z} _{3},$ $\mathbb {Z} _{2}$	abelsch
	$\mathbb {Z} _{3}\rtimes \mathbb {Z} _{8}$	$\mathbb {Z} _{12},$ $3\cdot \mathbb {Z} _{8},$ $\mathbb {Z} _{6},$ $\mathbb {Z} _{4},$ $\mathbb {Z} _{3},$ $\mathbb {Z} _{2}$	nichtabelsch
	SL(2,3) $\cong Q_{8}\rtimes \mathbb {Z} _{3}$	$Q_{8},$ $4\cdot \mathbb {Z} _{6},$ $3\cdot \mathbb {Z} _{4},$ $4\cdot \mathbb {Z} _{3},$ $\mathbb {Z} _{2}$	nichtabelsch
	$Q_{24}\cong \mathbb {Z} _{3}\times Q_{8}$	$\mathbb {Z} _{12},$ $2\cdot Q_{12},$ $3\cdot Q_{8},$ $\mathbb {Z} _{6},$ $7\cdot \mathbb {Z} _{4},$ $\mathbb {Z} _{3},$ $\mathbb {Z} _{2}$	nichtabelsch
	$D_{3}\times \mathbb {Z} _{4}\cong S_{3}\times \mathbb {Z} _{4}$	$\mathbb {Z} _{12},$ $Q_{12},$ $D_{6},$ $3\cdot \mathbb {Z} _{4}\times \mathbb {Z} _{2},$ $\mathbb {Z} _{6},$ $2\cdot D_{3},$ $4\cdot \mathbb {Z} _{4},$ $3\cdot D_{2},$ $\mathbb {Z} _{3},$ $7\cdot \mathbb {Z} _{2}$	nichtabelsch
	$D_{12}$	$\mathbb {Z} _{12},$ $2\cdot D_{6},$ $3\cdot D_{4},$ $\mathbb {Z} _{6},$ $4\cdot D_{3},$ $\mathbb {Z} _{4},$ $6\cdot D_{2},$ $\mathbb {Z} _{3},$ $13\cdot \mathbb {Z} _{2}$	nichtabelsch
	$Q_{12}\times \mathbb {Z} _{2}\cong (\mathbb {Z} _{3}\rtimes \mathbb {Z} _{4})\times \mathbb {Z} _{2}$	$\mathbb {Z} _{6}\times \mathbb {Z} _{2},$ $2\cdot Q_{12},$ $3\cdot \mathbb {Z} _{4}\times \mathbb {Z} _{2},$ $3\cdot \mathbb {Z} _{6},$ $6\cdot \mathbb {Z} _{4},$ $D_{2},$ $\mathbb {Z} _{3},$ $3\cdot \mathbb {Z} _{2}$	nichtabelsch
	$(\mathbb {Z} _{6}\times \mathbb {Z} _{2})\rtimes \mathbb {Z} _{2}\cong \mathbb {Z} _{3}\rtimes D_{4}$	$\mathbb {Z} _{6}\times \mathbb {Z} _{2},$ $Q_{12},$ $D_{3},$ $3\cdot D_{4},$ $3\cdot \mathbb {Z} _{6},$ $2\cdot D_{3},$ $3\cdot \mathbb {Z} _{4},$ $4\cdot D_{2},$ $\mathbb {Z} _{3},$ $9\cdot \mathbb {Z} _{2}$	nichtabelsch
	$D_{4}\times \mathbb {Z} _{3}$	$\mathbb {Z} _{12},$ $2\cdot \mathbb {Z} _{6}\times \mathbb {Z} _{2},$ $D_{4},$ $5\cdot \mathbb {Z} _{6},$ $\mathbb {Z} _{4},$ $2\cdot D_{2},$ $\mathbb {Z} _{3},$ $5\cdot \mathbb {Z} _{2}$	nichtabelsch
	$Q_{8}\times \mathbb {Z} _{3}$	$3\cdot \mathbb {Z} _{12},$ $Q_{8},$ $\mathbb {Z} _{6},$ $3\cdot \mathbb {Z} _{4},$ $\mathbb {Z} _{3},$ $\mathbb {Z} _{2}$	nichtabelsch
	$S_{4}$	$A_{4},$ $3\cdot D_{4},$ $4\cdot D_{3},$ $3\cdot \mathbb {Z} _{4},$ $4\cdot D_{2},$ $4\cdot \mathbb {Z} _{3},$ $9\cdot \mathbb {Z} _{2}$	nichtabelsch
	$A_{4}\times \mathbb {Z} _{2}$	$A_{4},$ $\mathbb {Z} _{2}^{3},$ $4\cdot \mathbb {Z} _{6},$ $7\cdot D_{2},$ $4\cdot \mathbb {Z} _{3},$ $7\cdot \mathbb {Z} _{2}$	nichtabelsch
	$D_{6}\times \mathbb {Z} _{2}$	$\mathbb {Z} _{6}\times \mathbb {Z} _{2},$ $6\cdot D_{6},$ $3\cdot \mathbb {Z} _{2}^{3},$ $3\cdot \mathbb {Z} _{6},$ $4\cdot D_{3},$ $19\cdot D_{2},$ $\mathbb {Z} _{3},$ $15\cdot \mathbb {Z} _{2}$	nichtabelsch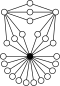

Einfache Struktursätze

Die folgenden Aussagen sind sehr elementare Struktursätze, deren Auswirkung sich deutlich in obiger Liste widerspiegelt.

Ist $p$ eine Primzahl, so ist jede Gruppe der Ordnung $p$ isomorph zur zyklischen Gruppe $\mathbb {Z} _{p}$ .^[2]

Ist $p$ eine Primzahl, so ist jede Gruppe der Ordnung $p^{2}$ abelsch,^[3] genauer isomorph zur zyklischen Gruppe $\mathbb {Z} _{p^{2}}$ oder zum direkten Produkt $\mathbb {Z} _{p}\times \mathbb {Z} _{p}$ .^[4]

Ist $p$ eine Primzahl, so ist jede Gruppe der Ordnung $2p$ isomorph zur zyklischen Gruppe $\mathbb {Z} _{2p}$ oder zur Diedergruppe $D_{p}$ .^[5]

Sind $p$ und $q$ Primzahlen mit $q<p$ und ist $q$ kein Teiler von $p-1$ , dann ist jede Gruppe der Ordnung $pq$ isomorph zur zyklischen Gruppe $\mathbb {Z} _{pq}$ .^[6]

„The SmallGroups Library“

Das Computeralgebrasystem GAP enthält die Programmbibliothek SmallGroups Library, die eine Beschreibung von Gruppen kleiner Ordnung enthält. Diese sind alle bis auf Isomorphie aufgelistet. Momentan (GAP Version 4.8.8) enthält die Bibliothek Gruppen folgender Ordnung:

alle der Ordnung bis $2000$ , außer den $49.487.365.422$ Gruppen der Ordnung $1024$ (bleiben $423.164.062$ Gruppen);
alle Gruppen, deren Ordnung $n$ für keine Primzahl $p$ von $p^{3}$ geteilt wird, für $n\leq 50.000$ ( $395.703$ Gruppen);
alle der Ordnung $p^{7}$ , wobei $p$ eine der Primzahlen $3,5,7$ oder $11$ ist ( $907.489$ Gruppen);
alle der Ordnung $p^{n}$ mit einer beliebigen Primzahl $p$ und $n\leq 6$ ;
alle der Ordnung $q^{n}p$ mit $q^{n}$ teilt $2^{8},3^{6},5^{5}$ oder $7^{4}$ und $p$ ist eine beliebige von $q$ verschiedene Primzahl;
alle Gruppen, deren Ordnung $n$ für keine Primzahl $p$ von $p^{2}$ geteilt wird (d. h. $n$ ist quadratfrei);
alle Gruppen, deren Ordnung $n$ in höchstens drei Primzahlen zerlegbar ist.

Diese Bibliothek wurde von Hans Ulrich Besche, Bettina Eick und Eamonn O’Brien erstellt.^[7]

Einzelnachweise

↑ In der Liste der Untergruppen werden die trivialen Untergruppen (die einelementige Gruppe und die Gruppe selbst) nicht aufgelistet.
↑ Bertram Huppert: Endliche Gruppen I. Springer-Verlag, 1967, Kap. I, § 2, Satz 2.10.
↑ Bertram Huppert: Endliche Gruppen I. Springer-Verlag (1967), Kap. I, § 6, Satz 6.10.
↑ Kurt Meyberg: Algebra Teil 1. Carl Hanser Verlag, 1980, ISBN 3-446-13079-9, Satz 2.2.12.
↑ Kurt Meyberg: Algebra Teil 1. Carl Hanser Verlag (1980), ISBN 3-446-13079-9, Beispiel 2.2.11 e.
↑ Bertram Huppert: Endliche Gruppen I. Springer-Verlag (1967), Kap. I, § 8, Satz 8.10.
↑ The SmallGroups library. Bei: www.gap-system.org.

Weblinks

Thomas Keilen: Endliche Gruppen. (PS, dt.; GZIP; 202 kB), siehe § 15: Klassifikation der Gruppen bis Ordnung 23.
Eric W. Weisstein: Finite Group. In: MathWorld (englisch).
Ausführliche Klassifikation der Gruppen bis Ordnung 28 (englisch).

[ug-1] In der Liste der Untergruppen werden die trivialen Untergruppen (die einelementige Gruppe und die Gruppe selbst) nicht aufgelistet.

[2] Bertram Huppert: Endliche Gruppen I. Springer-Verlag, 1967, Kap. I, § 2, Satz 2.10.

[3] Bertram Huppert: Endliche Gruppen I. Springer-Verlag (1967), Kap. I, § 6, Satz 6.10.

[4] Kurt Meyberg: Algebra Teil 1. Carl Hanser Verlag, 1980, ISBN 3-446-13079-9, Satz 2.2.12.

[5] Kurt Meyberg: Algebra Teil 1. Carl Hanser Verlag (1980), ISBN 3-446-13079-9, Beispiel 2.2.11 e.

[6] Bertram Huppert: Endliche Gruppen I. Springer-Verlag (1967), Kap. I, § 8, Satz 8.10.

[7] The SmallGroups library. Bei: www.gap-system.org.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Fahrer / Team für die Suche eingeben: