Le-Sage-Gravitation
Die Le-Sage-Gravitation ist eine einfache mechanische Gravitationserklärung, die das Gravitationsgesetz von Newton begründen sollte. Sie wurde von Nicolas Fatio de Duillier (1690) und Georges-Louis Le Sage (1748) entworfen.
Da Fatios Arbeit weithin unbekannt war und unveröffentlicht blieb, war es Le Sages Version der Theorie, die gegen Ende des 19. Jahrhunderts im Zusammenhang mit der damals neu entwickelten kinetischen Theorie der Gase zum Gegenstand erwachenden Interesses wurde. Obwohl einige Forscher außerhalb des Mainstreams die Theorie weiterhin untersuchen, wird sie vor allem aufgrund der von James Clerk Maxwell (1875) und Henri Poincaré (1908) hervorgebrachten Einwände als überholt und ungültig eingestuft.
Grundzüge der Theorie
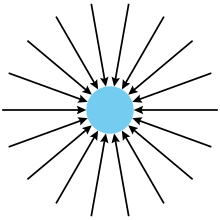
Keine Bewegung
Die Grundannahme der Theorie ist die Existenz eines Raumes, der weitgehend isotrop von einem Strahlungsfeld ausgefüllt ist, das aus diversen Teilchen (Korpuskeln) oder Wellen besteht. Diese bewegen sich mit konstanter, sehr hoher Geschwindigkeit geradlinig in alle möglichen Richtungen. Trifft ein Teilchen auf einen Körper, überträgt es einen Impuls auf ihn. Ist nur ein Körper A vorhanden, ist dieser einem gleichmäßigen Druck ausgesetzt, er befindet sich also aufgrund der in alle Richtungen wirkenden Stöße in einem Kräftegleichgewicht und wird sich nicht bewegen (siehe Abbildung B1).

Körper „ziehen“ sich an
Ist jedoch ein zweiter Körper B vorhanden, wirkt dieser wie ein Schirm, denn aus Richtung B wird A von weniger Teilchen getroffen, als von der anderen Seite, wobei das Gleiche auch umgekehrt gilt. A und B verschatten einander (B2) und dadurch entsteht ein Unterdruck auf den einander zugewandten Seiten. Es entsteht somit eine scheinbar anziehende Kraft, die genau in Richtung des jeweils anderen Körpers wirkt. Die Theorie basiert daher nicht auf dem Konzept der Anziehung, sondern wird zur Klasse der Drucktheorien oder kinetischen Gravitationerklärungen gezählt.
- Natur der Kollisionen

Wenn die Kollisionen zwischen Körper A und den Teilchen völlig elastisch sind, wäre die Intensität der reflektierten Teilchen genauso hoch wie die der einströmenden, sodass keine Kraft in Richtung A resultieren würde. Das Gleiche würde passieren, wenn ein zweiter Körper B vorhanden wäre, der als Schirm für Teilchen wirken würde, die in Richtung A fliegen. Die zwischen den Körpern reflektierten Teilchen würden den Schatteneffekt vollkommen aufheben. Um also eine gravitative Wirkung zwischen den Körpern zuzulassen, muss die kinetische Energie der Teilchen von der Materie vollständig oder zumindest teilweise absorbiert werden, oder sie müssen derart modifiziert werden, dass ihr Impuls nach der Kollision abgenommen hat: Nur dann überwiegt der Impuls der einströmenden Teilchen gegenüber dem Impuls der von den Körpern reflektierten Teilchen (B3).
- Proportionalität zu 1/r²

Stellt man sich um einen Körper eine Kugeloberfläche (Sphäre) vor, die sowohl von den reflektierten als auch von den einströmenden Teilchen durchquert werden muss, wird ersichtlich, dass die Größe der Sphäre proportional zum Quadrat der Entfernung zunimmt. Die Anzahl der betreffenden Teilchen in diesen größer werdenden Abschnitten bleibt jedoch gleich und somit sinkt deren Dichte. Die Gravitationswirkung verhält sich also, dem Abstandsgesetz gemäß, umgekehrt zum Quadrat der Entfernung zu den jeweiligen Massen (B4). Diese Analogie zu optischen Effekten wie der Abnahme der Strahlungsintensität mit 1/r² oder der Schattenbildung wurde schon von Fatio und Le Sage angegeben.
- Proportionalität zur Masse
Aus dem bisher Dargelegten ergibt sich vorerst nur eine Kraft, deren Stärke proportional zur Oberfläche oder dem Volumen ist. Die Gravitation ist jedoch neben dem Volumen auch von der Dichte und somit von der Masse abhängig. Um also diese beobachtete Proportionalität zur Masse zu erreichen, wurde angenommen, dass die Materie größtenteils aus leerem Raum besteht und die als sehr klein angenommenen Teilchen die Körper mühelos durchdringen können. Das heißt, die Teilchen durchdringen die Körper, wechselwirken mit allen Bestandteilen der Materie, werden teilweise abgeschirmt oder absorbiert und treten geschwächt wieder hinaus. Dadurch wird bei Annahme entsprechender Durchdringungsfähigkeit zumindest innerhalb einer bestimmten Messgenauigkeit eine der Masse proportionale Schattenwirkung der Körper erreicht. Das Ergebnis (B5): Zwei Körper verschatten einander und es ergibt sich ein analoges Bild zu B2.

Fatio

Nicolas Fatio de Duillier präsentierte 1690 die erste Fassung seiner Gedanken über Gravitation in einem Brief an Christiaan Huygens.[A 1] Unmittelbar darauf verlas er dessen Inhalt bei einer Sitzung der Royal Society in London. In den folgenden Jahren entwarf Fatio mehrere Manuskripte seines Hauptwerks De la Cause de la Pesanteur. Auch schrieb er 1731 ein in Latein abgefasstes Lehrgedicht mit demselben Thema.[C 1] Einige Fragmente dieser Manuskripte wurden später von Le Sage erworben, der sie zu veröffentlichen versuchte, aber damit keinen Erfolg hatte. Und so dauerte es bis 1929, als Karl Bopp eine Kopie eines vollständigen Manuskripts veröffentlichte.[A 2] Eine weitere Version der Theorie wurde 1949 von Bernard Gagnebin veröffentlicht, der aus den Fragmenten von Le Sage das Werk zu rekonstruieren versuchte.[A 3] Die folgende Beschreibung beruht hauptsächlich auf der Bopp-Edition (die u. a. die „Probleme I–IV“ beinhaltet) und der Darstellung von Zehe.[C 2]
Einige Aspekte der Theorie
Fatios Pyramide (Problem I)
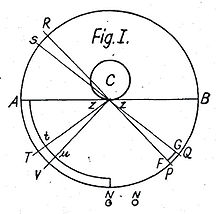
Fatio nahm an, dass das Universum von winzigen Teilchen ausgefüllt sei, die sich unterschiedslos und geradlinig mit sehr großer Geschwindigkeit in alle Richtungen bewegen. Um seine Gedanken zu veranschaulichen, benutzte er folgendes Bild: Es sei ein Objekt C gegeben, auf dem sich eine unendlich kleine Fläche zz befindet. Diese Fläche zz sei der Mittelpunkt eines Kreises. Innerhalb dieses Kreises zeichnete Fatio die Pyramide PzzQ, in der einige Teilchen in Richtung zz strömen, und ebenso einige Teilchen, die von C bereits reflektiert wurden, in Gegenrichtung strömen. Fatio nahm an, dass die durchschnittliche Geschwindigkeit und somit auch die Impulse der reflektierten Teilchen geringer seien als die der einströmenden. Das Resultat ist ein Strom, der alle Körper in Richtung zz treibt. Einerseits bleibt die Geschwindigkeit des Stromes konstant, andererseits nimmt in größerer Nähe zu zz dessen Dichte zu. Deshalb ist aufgrund der geometrischen Verhältnisse seine Intensität proportional zu 1/r², wobei r der Abstand zu zz ist. Weil unendlich viele solcher Pyramiden um C vorstellbar sind, gilt diese Proportionalität für den gesamten Bereich um C.
Reduzierte Geschwindigkeit
Um die Behauptung zu rechtfertigen, dass sich die Teilchen mit verminderter Geschwindigkeit nach der Reflexion bewegen, unterbreitete Fatio folgende Vorschläge:
- Die gewöhnliche Materie, oder die Teilchen, oder beide sind unelastisch.
- Die Zusammenstöße sind vollkommen elastisch, aber die Teilchen sind nicht absolut hart, weshalb sie nach dem Stoß vibrieren und an Geschwindigkeit verlieren.
- Durch Reibung beginnen die Teilchen zu rotieren und verlieren ebenfalls an Geschwindigkeit.
Diese Passagen sind die unverständlichsten Teile von Fatios Theorie, weil er nie klar entscheidet, welche Art von Kollision zu bevorzugen ist. In der letzten Version der Theorie von 1743 kürzte er jedoch diese Passagen und schrieb einerseits den Teilchen perfekte Elastizität oder perfekte Federkraft zu, und andererseits der Materie unvollständige Elastizität, so dass die Teilchen mit geringerer Geschwindigkeit reflektiert werden. Der Geschwindigkeitsverlust wurde von Fatio äußerst gering angesetzt, um die Gravitationskraft über längere Zeiträume nicht merklich absinken zu lassen. Zusätzlich sah sich Fatio mit einem anderen Problem konfrontiert: Was passiert, wenn die Teilchen untereinander kollidieren? Unelastische Kollisionen würden, selbst wenn keine normale Materie anwesend ist, zu einem ständigen Absinken der Geschwindigkeit führen und deswegen ebenfalls die Gravitationskraft schwächen. Um dieses Problem zu vermeiden, nahm Fatio an, dass der Durchmesser der Teilchen sehr klein gegenüber ihrem gegenseitigen Abstand ist, und deswegen Begegnungen untereinander sehr selten sind.
Verdichtung
Um den Einwand zu entkräften, dass sich durch die geringere Teilchengeschwindigkeit eine Stauung um die Körper bilden könnte, erklärte Fatio, dass die reflektierten Teilchen tatsächlich langsamer seien als die Einströmenden. Daher haben die von außen einströmenden Teilchen zwar eine größere Geschwindigkeit, jedoch ebenso einen größeren Abstand untereinander. Umgekehrt sind die reflektierten Teilchen langsamer, was aber durch eine konstant bleibende Verdichtung ausgeglichen wird. Die Verdichtung ist also konstant und es kommt zu keiner Stauung. Fatio führte weiter aus, dass durch immer weitergehende Vergrößerung der Geschwindigkeit und Elastizität der Teilchen diese Verdichtung beliebig klein gemacht werden kann.
Durchlässigkeit der Materie

Um die Proportionalität zur Masse zu erklären, musste Fatio postulieren, dass normale Materie in alle Richtungen gleichmäßig durchlässig für die Teilchen ist. Er skizzierte dazu 3 Modelle:
- Er nahm an, dass Materie eine Anhäufung kleiner Kugeln sei, wobei deren Durchmesser verschwindend gering gegenüber ihrem gegenseitigen Abstand ist. Aber er verwarf diese Erklärung, weil die Kugeln dazu tendieren müssten, sich immer weiter einander zu nähern.
- Dann nahm er an, dass Kugeln durch Stäbe miteinander verbunden seien und ein Kristallgitter oder Netz bilden würden. Jedoch verwarf er auch dieses Modell, denn bei Vereinigung verschiedener Netze wäre an den Orten, wo sich die Kugeln sehr nahe beieinander befinden, keine gleichmäßige Durchdringung mehr möglich.
- Schließlich entfernte er auch die Kugeln und ließ einzig und allein die Stäbe des Netzes übrig, wobei er den Durchmesser der Stäbe verschwindend gering im Vergleich zu ihrem Abstand machte. So meinte er, eine maximale Durchdringbarkeit gewährleisten zu können.
Druck der Teilchen (Problem II)
Bereits 1690 nahm Fatio an, dass der Druck, der von den Teilchen auf eine ebene Fläche ausgeübt wird, den sechsten Teil des Drucks ausmacht, der bestünde, wenn alle Teilchen senkrecht zur Ebene ausgerichtet wären. Fatio erbrachte einen Beweis für diese Behauptung, indem er den Druck errechnete, der von den Teilchen auf einen bestimmten Punkt zz. ausgeübt wird. Er gelangte schließlich zur Formel , wobei die Dichte und die Geschwindigkeit der Teilchen ist. Diese Lösung ist sehr ähnlich der in der kinetischen Gastheorie bekannten Formel , die von Daniel Bernoulli 1738 gefunden wurde. Das war das erste Mal, dass die enge Verwandtschaft zwischen den beiden Theorien dargelegt wurde, und das bevor letztere überhaupt entwickelt wurde. Jedoch ist Bernoullis Wert doppelt so groß, weil Fatio für den Impuls bei der Reflexion nicht , sondern angesetzt hat. Sein Resultat wäre daher nur bei völlig unelastischen Stößen gültig. Fatio benutzte seine Lösung nicht nur zur Erklärung der Gravitation, sondern auch, um das Verhalten der Gase zu erklären. Er konstruierte ein Thermometer, das den Bewegungszustand der Luftmoleküle und damit die Wärme messen sollte. Jedoch im Gegensatz zu Bernoulli identifizierte Fatio die Bewegung der Luftmoleküle nicht mit der Wärme, sondern machte ein anderes Fluid dafür verantwortlich. Es ist jedoch nicht bekannt, ob Bernoulli von Fatio beeinflusst wurde.
Unendlichkeit (Problem III)
In diesem Abschnitt untersuchte Fatio den Begriff der Unendlichkeit im Zusammenhang mit seiner Theorie. Fatio rechtfertigte viele seiner Betrachtungen mit dem Umstand, dass verschiedene Phänomene unendlich kleiner und größer als andere sind und viele problematische Effekte der Theorie dadurch auf einen unmessbaren Wert verkleinert werden können. Beispielsweise der Durchmesser der Stäbe ist unendlich kleiner als deren Abstand zueinander; oder die Geschwindigkeit der Teilchen ist unendlich größer als die der Materie; oder der Geschwindigkeitsunterschied zwischen reflektierten und nicht reflektierten Teilchen ist unendlich klein.
Widerstand des Mediums (Problem IV)
Dies ist der mathematisch anspruchsvollste Teil von Fatios Theorie. Hier versuchte er den Strömungswiderstand der Teilchenströme für bewegte Körper zu berechnen. Es sei die Geschwindigkeit der Körper, die Geschwindigkeit der Teilchen und die Dichte des Ausbreitungsmediums. Im Fall und errechnete Fatio einen Widerstand von . Im Fall und verhält sich der Widerstand wie . Newton folgend, der aufgrund des nicht beobachteten Widerstandes in Bewegungsrichtung eine extrem geringe Dichte jeglichen Mediums forderte, verringerte Fatio die Dichte und folgerte, dies könne kompensiert werden durch Veränderung von umgekehrt proportional zur Quadratwurzel der Dichte. Dies folgt aus Fatios Druckformel . Nach Zehe war Fatios Versuch, mit Hilfe einer Erhöhung von den Widerstand in Bewegungsrichtung im Verhältnis zur Gravitationskraft gering zu halten, erfolgreich, denn der Widerstand ist in Fatios Modell proportional zu , aber die Gravitationskraft ist proportional zu .
Rezeption der Theorie

Fatio stand in Kontakt mit einigen der berühmtesten Wissenschaftler seiner Zeit. Einige von ihnen, wie Edmond Halley, Christiaan Huygens und Isaac Newton, unterzeichneten sein Manuskript.
Zwischen Newton und Fatio bestand eine enge persönliche Beziehung zwischen 1690 und 1693, wobei Newtons Bemerkungen über Fatios Theorie sehr unterschiedlich sind. Einerseits schrieb Newton 1692 in einer Stelle seiner eigenen Kopie der Principia, die von Fatio kopiert wurde:
„Bei dieser Art von Hypothesen gibt es eine einzige, durch die man die Schwere erklären kann, und die hat sich als erster Hr. Fatio, ein hochbegabter Mathematiker ausgedacht. Und um sie [die Hypothese] aufstellen zu können, ist Vakuum notwendig, da die dünnen Partikeln durch geradlinige, äußerst rasche und gleichförmig fortgesetzte Bewegungen nach allen Richtungen getragen werden müssen und sie [dabei] nur dort Widerstand spüren dürfen, wo sie auf gröbere Partikeln stoßen.“
Andererseits notierte David Gregory in seinem Tagebuch: „Mr. Newton und Mr. Halley lachen über Mr. Fatios Erklärung der Schwere“[C 2]. Dies wurde angeblich 1691 notiert. Jedoch unterscheidet sich die benutzte Tinte und Schreibfeder erheblich vom Rest des Blattes. Das legt nahe, dass der Eintrag erst später erfolgt ist. Fatio erkannte aber auch an, dass Newton eher dazu tendierte, die wahre Ursache der Gravitation im Willen Gottes zu sehen. Ab 1694 kühlte die Beziehung zwischen den beiden ab.
Christiaan Huygens war der Erste, der über Fatios Theorie informiert wurde, jedoch akzeptierte er sie nie und arbeitete an seiner eigenen Ätherwirbeltheorie weiter. Fatio glaubte, Huygens von der Widerspruchslosigkeit seiner Theorie überzeugt zu haben, jedoch bestritt Huygens dies in einem Brief an Gottfried Wilhelm Leibniz. Es fand auch eine kurze Korrespondenz zwischen Fatio und Leibniz statt, vor allem über mathematische Fragen, aber auch über Fatios Theorie. Leibniz kritisierte diese, weil Fatio einen leeren Raum zwischen den Teilchen voraussetzte, eine Annahme, die von Leibniz aus philosophischen Gründen zurückgewiesen wurde. Jakob I Bernoulli wiederum zeigte großes Interesse an Fatios Theorie und drängte ihn, diese in einem kompletten Manuskript niederzuschreiben, was auch tatsächlich von Fatio getan wurde. Bernoulli ließ davon eine Kopie anfertigen, die sich in der Universitätsbibliothek Basel befindet und die Basis für die Bopp-Edition bildet.
Trotz allem blieb Fatios Theorie weithin unbekannt, mit wenigen Ausnahmen wie Cramer und Le Sage, weil er nie fähig war, seine Arbeit zu veröffentlichen und er außerdem unter den Einfluss eines fanatischen Teils der Kamisarden kam und seine öffentliche Reputation dadurch vollständig verloren ging.
Cramer, Redeker
1731[A 4] veröffentlichte der Schweizer Mathematiker Gabriel Cramer eine Dissertation, an deren Ende die Zusammenfassung einer Theorie erscheint, welche identisch ist mit der von Fatio (inkl. Netzstruktur, Lichtanalogie und Abschattung etc.), jedoch ohne dass dessen Name aufgeführt wird. Es war Fatio jedoch bekannt, dass Cramer Zugriff auf eine Kopie seines Manuskripts hatte, deshalb warf er ihm vor, seine Theorie nur wiederholt zu haben, ohne sie zu verstehen. Es war ebenfalls Cramer, der später Le Sage auf Fatios Theorie aufmerksam machte. 1736[A 5] hatte Franz Albert Redeker, ein deutscher Arzt, ebenfalls eine sehr ähnliche Theorie aufgestellt.
Le Sage

Die erste Ausarbeitung der Theorie, Essai sur l'origine des forces mortes, wurde von Le Sage 1748 an die Akademie der Wissenschaften in Paris geschickt, jedoch abgelehnt und niemals publiziert.[C 1] 1749, also nach Ausarbeitung seiner eigenen Gedanken, wurde er von seinem Lehrer Cramer über die Existenz der Theorie Fatios unterrichtet und 1751 erfuhr er von Redekers Theorie. 1756 wurden erstmals in einer Zeitschrift die Gedanken Le Sages veröffentlicht[A 6] und 1758 sandte er mit Essai de Chymie Méchanique eine ausführlichere Variante seiner Theorie zu einem Preisausschreiben der Akademie der Wissenschaften. In dieser Arbeit versuchte er sowohl die Natur der Gravitation als auch die der chemischen Affinitäten zu erklären.[A 7] Er gewann den Preis zusammen mit einem Mitbewerber und sicherte sich dadurch die Aufmerksamkeit prominenter Zeitgenossen wie Leonhard Euler. Eine deutlich erweiterte Ausgabe dieses Essay wurde 1761 in wenigen Exemplaren gedruckt. Eine für das breitere Publikum zugängliche Arbeit, Lucrece Neutonien, wurde jedoch erst 1784 veröffentlicht.[A 8] Die ausführlichste Zusammenstellung der Theorie, Physique Mécanique des Georges-Louis Le Sage, wurde 1818 postum von Pierre Prevost veröffentlicht.[A 9]
Grundkonzept
Le Sage diskutierte die Theorie sehr detailliert, aber er fügte ihr nichts grundlegend neues hinzu und obwohl er in Besitz einiger Papiere Fatios war, erreichte er laut Zehe oft nicht dessen Niveau.[C 2]
- Le Sage nannte seine Gravitationsteilchen ultramundane Korpuskel, weil er glaubte, dass diese von weit außerhalb des bekannten Weltraums kommen. Die Verteilung dieser Ströme ist außerordentlich isotrop und die Gesetze der Ausbreitung entsprechen denen des Lichts.
- Er argumentierte, dass bei vollständig elastischen Materie-Teilchen-Kollisionen keine Gravitationskraft entstehen würde. So schlug er vor, dass die Teilchen und die Bestandteile der Materie absolut hart seien, was seiner Meinung nach eine komplizierte Form der Stoßwirkung impliziert, nämlich vollständig unelastisch senkrecht zur Oberfläche normaler Materie, und vollständig elastisch tangential zur Oberfläche. Er führte weiter aus, dass die reflektierten Teilchen deshalb durchschnittlich nur noch 2/3 der Geschwindigkeit von zuvor besitzen würden. Um unelastische Stöße zwischen den Teilchen zu vermeiden, nahm er wie Fatio an, dass deren Durchmesser sehr viel kleiner als ihr gegenseitiger Abstand sei.
- Der Widerstand der Teilchenströme ist proportional zu uv (wo v die Geschwindigkeit der Teilchen und u die des Körpers ist), hingegen die Gravitation ist proportional zu v². Daraus ergibt sich, dass das Verhältnis Widerstand/Gravitation beliebig klein gemacht werden kann durch Erhöhung von v. Er nahm für einige Zeit an, die Teilchen würden sich mit c (=Lichtgeschwindigkeit) bewegen, jedoch erhöhte er den Wert später erheblich auf 105·c.
- Um die Proportionalität zur Masse zu erhalten, entwarf er wie Fatio eine Hypothese, in der Materie eine Käfig- oder Gitterstruktur besitzt, wobei die Gitteratome selbst nur einen Durchmesser besitzen, welcher 107 mal kleiner als ihr gegenseitiger Abstand ist. Die Gitteratome selbst sind ebenfalls durchlässig, wobei ihre Stäbe ungefähr 1020 mal so lang als breit sind. Dadurch könnten die Teilchen praktisch ungehindert durchdringen.
- Le Sage versuchte den Abschattungsmechanismus auch zur Erklärung chemischer Effekte zu benutzen, indem er die Existenz vieler verschiedener ultramundaner Teilchenarten von verschiedener Größe postulierte (B9).

Rezeption der Theorie
Le Sages Ideen wurden zu seiner Zeit nicht sehr positiv aufgenommen, außer von einigen seiner gelehrten Freunde wie Pierre Prevost, Charles Bonnet, Jean-André Deluc und Simon L’Huilier. Diese erwähnten und beschrieben Le Sages Theorie in ihren Büchern und Artikeln, welche von ihren Zeitgenossen als sekundäre Quellen benutzt wurden – vor allem wegen des Mangels an veröffentlichten Papieren von Le Sage selbst.
- Euler, Daniel Bernoulli, Boscovich
Leonhard Euler merkte 1761 einmal an, dass Le Sages Modell unendlich besser als die Erklärungen anderer Autoren sei, und hier alle Einwände aufgelöst seien. Später meinte er jedoch, dass die Lichtanalogie keine Bedeutung für ihn habe, da er an die Wellennatur des Lichtes glaubte. Nach weiteren Betrachtungen lehnte er das Modell generell ab und schrieb 1765 an Le Sage:
« Je sens encore une-grande répugnance pur cos corpuscules ultra mondains, et j’aimerais toujours mieux d’avouer mon ignorance sur la cause de la gravite, que de recourir a des hypothèses étranges. »
„Sie müssen mich entschuldigen, wenn ich eine große Abneigung gegen Ihre ultramundanen Korpuskel habe, und ich werde es immer vorziehen, meine Unkenntnis über die Ursache für Schwerkraft zu gestehen, als auf solch fremdartige Hypothesen zurückzugreifen.“
Daniel Bernoulli war 1767 angetan von der Ähnlichkeit zwischen Le Sages Modell und seinen eigenen Gedanken zur kinetischen Theorie der Gase. Jedoch war Bernoulli selbst der Meinung, dass seine eigene Gastheorie nur Spekulation sei, wobei das in noch stärkerem Ausmaß auf Le Sages Theorie zuträfe. Wie sich allerdings im 19. Jahrhundert herausstellte, war Bernoullis Gastheorie im Prinzip korrekt. (S. 30)[C 4]
Rugjer Josip Bošković erklärte 1771, dass Le Sages Theorie die erste war, welche die Gravitation tatsächlich mit mechanischen Mitteln erklären könne. Jedoch verwarf er das Modell wegen der enormen und ungenutzten Quantität ultramundaner Materie. Zusätzlich lehnte Boscovich die Existenz unmittelbarer Kontaktwirkungen ab und schlug stattdessen abstoßende und anziehende Fernwirkungen vor. John Playfair beschrieb Boscovichs Argumente so:[C 5]
“An immense multitude of atoms, thus destined to pursue their never ending journey through the infinity of space, without changing their direction, or returning to the place from which they came, is a supposition very little countenanced by the usual economy of nature. Whence is the supply of these innumerable torrents; must it not involve a perpetual exertion of creative power, infinite both in extent and in duration?”
„Eine immense Anzahl an Atomen, bestimmt dazu ihrer niemals endenden Reise durch die Unendlichkeit des Raumes nachzugehen, ohne ihre Richtung zu verändern, oder jemals zu ihrem Ausgangsort zurückzukehren, ist eine Annahme, die sehr geringe Übereinstimmung mit der üblichen Ökonomie der Natur hat. Wo ist die Quelle dieser unzähligen Ströme; schließt das nicht eine immer währende Ausübung von kreativer Kraft ein, unendlich sowohl in der Ausdehnung als auch der Dauer?“
- Lichtenberg, Schelling
Georg Christoph Lichtenberg glaubte ursprünglich wie René Descartes, dass jede Erklärung der Naturphänomene auf geradliniger Bewegung und unmittelbarer Kontaktwirkung beruhen müsse, und Le Sages Theorie erfüllte diese Anforderungen.[A 10] Er nahm Bezug zu Le Sages Theorie in seinen Vorlesungen über Physik an der Universität von Göttingen und schrieb 1790 über Le Sages Theorie:
„Ist es ein Traum, so ist es der größte und erhabenste der je ist geträumt worden, und womit wir eine Lücke in unseren Büchern ausfüllen können, die nur durch einen Traum ausgefüllt werden kann“
Jedoch um 1796 änderte Lichtenberg seine Meinung, nachdem er mit der Argumentation Immanuel Kants konfrontiert wurde, welcher jeden Versuch kritisierte, Anziehung auf Abstoßung zurückzuführen. Nach Kant ist jede Form von Materie unendlich teilbar, woraus sich ergibt, dass die bloße Existenz von ausgedehnter Materie die Existenz von anziehenden Kräften erfordert, welche die einzelnen Teile zusammenhält. Diese Kraft kann jedoch nicht durch Stöße einer umgebenden Materie begründet werden, da ja die Teile dieser stoßenden Materie selbst wieder zusammengehalten werden müssten. Um diesen Zirkelschluss zu vermeiden, postulierte Kant neben einer abstoßenden Kraft die Notwendigkeit einer fundamentalen anziehenden Kraft.[A 11] Friedrich Wilhelm Joseph von Schelling wiederum lehnte Le Sages Modell wegen dessen mechanischen Materialismus ab, wogegen Schelling eine sehr idealistische Philosophie vertrat.[A 12]
- Laplace
Teilweise unter Berücksichtigung von Le Sages Theorie versuchte Pierre-Simon Laplace um 1805 die Geschwindigkeit zu bestimmen, mit der sich ein solches Medium bewegen muss, um im Einklang mit den astronomischen Beobachtungen zu bleiben. Er errechnete, dass die Geschwindigkeit der Gravitation zumindest 100 Millionen Mal größer als die Lichtgeschwindigkeit sein müsse, um Unregelmäßigkeiten in der Mondumlaufbahn zu vermeiden. Dies war für Laplace und andere überhaupt ein Grund anzunehmen, dass die Newtonsche Gravitation auf Fernwirkung beruhe und Nahwirkungsmodelle wie das von Le Sage nicht funktionieren können.[A 13]
Kinetische Theorie
Da die Theorien von Fatio, Cramer und Redeker weithin unbekannt blieben, war es Le Sages Theorie, die aufgrund der Entwicklung der kinetischen Gastheorie durch Clausius, Kelvin und Maxwell eine Neubelebung in der zweiten Hälfte des 19. Jahrhunderts erfuhr.
- Leray
Da Le Sages Teilchen nach den Kollisionen an Geschwindigkeit verlieren, müsste aufgrund des Energieerhaltungssatzes eine große Menge an Energie in interne Energiemodi der Körper konvertiert werden. Dieses Problem ansprechend, entwarf P. Leray 1869 eine Teilchentheorie, in welcher er annimmt, dass die absorbierte Energie von den Körpern teils zur Erzeugung von Wärme, teils zur Erzeugung des Magnetismus benutzt wird. Er spekulierte, dass dies eine mögliche Antwort auf die Frage sei, woher die Energie der Sterne kommt.[A 14]
- Kelvin, Tait

Le Sages eigenes Modell wurde vor allem durch die Arbeit von Lord Kelvin 1872 im Rahmen der kinetischen Gastheorie modernisiert. Nach einer Zusammenfassung der Theorie erkannte Kelvin, dass die absorbierte Energie ein sehr viel größeres Problem darstellt, als Leray glaubte. Die dabei erzeugte Wärme würde zum Verglühen jedes Körper in Sekundenbruchteilen führen. Deswegen schilderte Kelvin einen Mechanismus, welcher in abgewandelter Form bereits von Fatio 1690 entwickelt worden war. Kelvin glaubte, dass die Teilchen nach der Kollision zwar eine Einbuße ihrer translatorischen Energiekomponente erleiden, also langsamer würden, dafür stärker vibrieren und rotieren. Die getroffenen Körper würden sich nicht erhitzen, sondern die Teilchen selbst würden nach dem Stoß die Energie in Form von erhöhter Vibration und Rotation wieder mit sich forttragen. Dies ist im Zusammenhang mit Kelvins Theorie einer Wirbelnatur der Materie zu verstehen. Basierend auf seiner Auslegung der Prinzipien von Clausius, wonach das Verhältnis zwischen den 3 Energiemodi in einem Gas konstant bleibt, nahm er an, dass die Teilchen über kosmische Distanzen hinweg ihre ursprüngliche Energiekonfiguration durch Kollisionen mit anderen Teilchen wiedergewinnen würden und somit die Gravitationswirkung nicht mit der Zeit abnimmt. Kelvin glaubte, dass es deswegen möglich ist, die Teilchen als praktisch unerschöpfliche Energiequelle zu nutzen und damit eine Art perpetuum mobile zu konstruieren. Aus thermodynamischen Gründen ist eine solche Konstruktion jedoch nicht möglich und Kelvins Auslegung der Theorie von Clausius musste verworfen werden.[A 15]
Im Anschluss an Kelvin nannte Peter Guthrie Tait 1876 die Le Sage Theorie die einzig plausible Erklärung der Gravitation, welche bis dahin gefunden wurde.[A 16] Er sagte weiter:
“The most singular thing about it is that, if it be true, it will probably lead us to regard all kinds of energy as ultimately Kinetic.”
„Das bemerkenswerteste daran [an Le Sages Theorie] ist, dass wenn sie richtig ist, sie uns möglicherweise dazu bringen wird, alle Energieformen letztendlich als kinetisch zu betrachten.“
- Preston
Samuel Tolver Preston zeigte, dass viele der von Le Sage eingeführten Postulate für die Teilchen, wie die geradlinige Bewegung, spärliche Interaktion etc., unter der Annahme zusammengefasst werden können, dass sie sich – auf kosmischer Ebene – wie ein Gas verhalten, dessen Teilchen eine extrem große mittlere freie Weglänge besitzen. Preston akzeptierte auch Kelvins Vorschlag der internen Bewegungsmodi der Teilchen. Er veranschaulichte Kelvins Modell, indem er es mit der Kollision eines Stahlringes und eines Amboss verglich. Dieser würde nicht sonderlich beeinträchtigt werden, jedoch der Stahlring würde sehr starken Vibrationen unterworfen sein und deswegen an Geschwindigkeit verlieren. Er argumentierte, dass die mittlere freie Weglänge der Teilchen zumindest die Distanz zwischen den Planeten ausmacht. Bei größeren Distanzen könnten die Teilchen (im Sinne Kelvins) ihre ursprüngliche translatorische Bewegungsgröße durch Kollisionen mit anderen Teilchen wiedergewinnen. Deswegen war er überhaupt der Meinung, ab einer bestimmten Entfernung würde die gravitative Wirkung zwischen 2 Körpern nicht mehr auftreten, und das unabhängig von ihrer Größe.[A 17] Paul Drude schlug 1897 vor, dass dies eine Möglichkeit wäre, den Theorien von Carl Gottfried Neumann und Hugo von Seeliger, welche eine Absorption der Gravitation im leeren Raum vorschlugen, eine physikalische Grundlage zu geben.[C 6]
- Maxwell

Eine Besprechung der Le-Sage-Kelvin Theorie wurde 1875 von James Clerk Maxwell in der Encyclopaedia Britannica veröffentlicht.[A 18] Nach der Beschreibung des grundlegenden Mechanismus schrieb er:
“Here, then, seems to be a path leading towards an explanation of the law of gravitation, which, if it can be shown to be in other respects consistent with facts, may turn out to be a royal road into the very arcana of science.”
„Hier scheint ein Pfad zu sein, der in Richtung einer Erklärung der Gravitation führt, welcher – wenn gezeigt werden kann, dass er auch in anderer Hinsicht konsistent mit den Fakten ist – sich als der königliche Weg in das eigentliche Geheimnis der Wissenschaft erweisen kann.“
Dennoch verwarf er das Modell, da gemäß den Gesetzen der Thermodynamik die kinetische Energie der Körper sich derjenigen der Teilchen angleichen müsste, wobei die Energie der letzteren sehr viel größer sei, als die der Moleküle der Körper. Als Ergebnis dieses Prozesses müssten die Körper in kürzester Zeit verglühen. Kelvins Lösung würde zwar das mechanische Gleichgewicht zwischen den Systemen erhalten, jedoch nicht das thermodynamische. Er schloss:
“We have devoted more space to this theory than it seems to deserve, because it is ingenious, and because it is the only theory of the cause of gravitation which has been so far developed as to be capable of being attacked and defended.”
„Wir haben dieser Theorie mehr Raum gewidmet als sie es zu verdienen scheint, weil sie geistreich ist und weil sie die einzige Theorie über die Ursache der Gravitation ist, die bis jetzt so weit entwickelt ist, um tauglich für Angriffe und Verteidigungen zu sein.“
Maxwell führte weiter aus, dass die Theorie dadurch einen enormen Aufwand an externer Energie beanspruche und deswegen die Energieerhaltung als fundamentales Prinzip der Natur verletze. Preston antwortete auf Maxwells Kritik mit dem Argument, dass die kinetische Energie der einzelnen Teilchen beliebig klein gemacht werden kann, indem ihre Anzahl vergrößert wird und deswegen der Energieunterschied nicht so groß wie von Maxwell angenommen sei. Jedoch wurde diese Frage später von Poincaré detaillierter behandelt, welcher zeigte, dass das thermodynamische Problem weiterhin ungelöst blieb.
- Isenkrahe
Caspar Isenkrahe veröffentlichte sein Modell erstmals 1879, wobei bis 1915 viele weitere Schriften folgten. Im Gegensatz zu seinen Vorgängern erarbeitete er eine detailliertere Anwendung der kinetischen Gastheorie im Le Sage Modell. Wie Le Sage argumentierte er, dass die Teilchen absolut hart seien und deswegen die Stöße elastisch tangential, und unelastisch senkrecht zur Oberfläche der Körper sind und erhielt den gleichen Faktor von 2/3. Jedoch war er der Meinung, dass bei den Stößen ein echter Energieverlust eintrete, und dass deswegen der Energieerhaltungssatz in diesem Bereich nicht mehr anwendbar sei, was jedoch mit den thermodynamischen Grundsätzen unvereinbar war und ist. Isenkrahe erklärte, dass die Energieverluste aufgrund der geringen Anzahl an Kollisionen vernachlässigbar seien. Er kritisierte das Kelvin-Preston-Modell, weil er keinen Grund sah, warum die reflektierten Teilchen stärker vibrieren und rotieren sollten, denn es sei schließlich genauso gut das Gegenteil möglich. Aus der Tatsache, dass nur bei enormer Porosität der Materie die Proportionalität der Gravitation zur Masse aufrechterhalten werden kann, zog er den Schluss, dass der Effekt der Wärmeausdehnung die Körper schwerer machen müsse. Das geschieht deshalb, weil bei geringerer Dichte eine gegenseitige Abschirmung der Körpermoleküle seltener ist.[A 19]
- Rysanek
In einem anderen Modell entwickelte Adalbert Rysanek 1887 eine sehr sorgfältige Analyse der Phänomene, wobei er Maxwells Gesetz der Teilchengeschwindigkeiten in einem Gas berücksichtigte. Er unterschied zwischen einem Lichtäther und einer Gravitationsäther, da nach seinen Berechnungen die Abwesenheit eines Widerstands des Mediums bei der Umlaufbahn des Neptun eine untere Geschwindigkeit der Gravitationsteilchen von 5 · 1019 cm/s erfordert. Ähnliche Argumente wurden von Bock[A 20] vorgebracht. Wie Leray argumentierte Rysanek, dass die absorbierte Energie die Herkunft der Sonnenenergie erklären könne, wobei zusätzlich die absorbierte Energie ebenfalls an den Lichtäther weitergegeben werde könnte. Jedoch waren diese Angaben zu ungenau, um die Einwände von Maxwell zu entkräften.[A 21]
- du Bois-Reymond
1888 argumentierte Paul du Bois-Reymond gegen die Le-Sage-Theorie, dass um eine exakte Massenproportionalität wie in Newtons Modell zu erreichen (was eine unendlich große Durchdringbarkeit voraussetzt), der Druck der Teilchen ebenfalls unendlich groß sein muss. Er berücksichtigte zwar das Argument, dass die Massenproportionalität für sehr große Massen keinesfalls experimentell bestätigt sei, jedoch sah er keinen Grund, die bewährte newtonsche Fernwirkung aufgrund einer bloßen Hypothese aufzugeben. Er führte (wie andere vor ihm) aus, dass unmittelbare Stoßwirkungen selbst völlig unerklärlich seien und im Grund ebenfalls auf Fernwirkungen beruhen. Das Hauptbestreben einer solchen Theorie, alle Fernwirkungen auszuschließen, sei somit nicht verwirklichbar.[A 22]
Wellen
Neben der kinetischen Gastheorie wurden auch die im 19. Jahrhundert verwendeten Konzepte von Wellen im Äther zur Konstruktion ähnlicher Modelle benutzt. Danach wurde versucht, Le Sages Teilchen durch elektromagnetische Wellen zu ersetzen. Dies geschah in Verbindung mit der Elektronentheorie jener Zeit, in welcher die elektrische Natur der gesamten Materie angenommen wurde.
- Keller, Boisbaudran
1863 veröffentlichten F. und E. Keller eine Gravitationstheorie, in welcher sie einen Le-Sage-Mechanismus in Verbindung mit Longitudinalwellen des Äthers entwarfen. Sie nahmen an, dass diese Wellen sich in alle Richtungen ausbreiten und einigen Impuls nach dem Aufschlag auf die Körper verlieren würden, so dass zwischen den Körpern der Druck etwas geringer ausfällt, als von den Außenseiten.[A 23] 1869 erstellte Lecoq de Boisbaudran praktisch dasselbe Modell wie Leray (Wärme, Magnetismus), jedoch ersetzte er wie Keller die Teilchen durch Longitudinalwellen.[A 24]
- Lorentz

Hendrik Antoon Lorentz versuchte 1900 die Gravitation mit seiner Lorentz-Äthertheorie zu vereinbaren. Dabei vermerkte er, dass Le Sages Teilchentheorie nicht mit ihr verträglich sei. Jedoch führte die Entdeckung, dass elektromagnetische Wellen eine Art Strahlungsdruck erzeugen, und in Form von Röntgenstrahlen Materie relativ einfach durchdringen können, Lorentz auf den Gedanken, die Teilchen durch extrem hochfrequente EM-Strahlen zu ersetzen. Er konnte tatsächlich zeigen, dass durch Abschattung eine anziehende Kraft zwischen geladenen Teilchen (welche als Grundbausteine der Materie aufgefasst wurden) entsteht. Das geschieht allerdings nur unter der Voraussetzung, dass die gesamte Strahlungsenergie absorbiert wird. Das war dasselbe fundamentale Problem wie in den Teilchenmodellen. Deswegen verwarf er das Modell und wie er weiter ausführte, wären auch Bahninstabilitäten aufgrund der endlichen Ausbreitungsgeschwindigkeit der Wellen zu erwarten.[A 25]
Auf das Thema zurückkommend diskutierte Lorentz 1922 die Erkenntnisse von Martin Knudsen über das Verhalten von Gasen mit sehr hoher freier Weglänge, welche eine Zusammenfassung sowohl von Le Sages Teilchentheorie als auch seiner eigenen elektromagnetischen Variante folgte. Er wiederholte jedoch seinen Schluss aus 1900: Ohne Absorption gibt es keine Gravitation in dieser Theorie.[A 26]
- J.J. Thomson
1904[A 27] zog Joseph John Thomson ein Le-Sage-Modell auf EM-Basis in Betracht, in dem die Strahlung weit durchdringender als gewöhnliche Röntgenstrahlung ist. Er argumentierte, dass die von Maxwell angeführte Erwärmung vermieden werden kann, wenn angenommen wird, dass die absorbierte Strahlung nicht in Wärme verwandelt, sondern als sekundäre Strahlung von noch viel größerer Durchdringungsfähigkeit re-emittiert wird. Er bemerkte, dass dieser Prozess erklären könnte, woher die Energie der radioaktiven Substanzen kommt. Jedoch meinte er, eine interne Ursache für die Radioaktivität sei sehr viel wahrscheinlicher. 1911 kam Thomson auf dieses Thema zurück und erklärte, dass diese sekundäre Strahlung sehr ähnlich dem Effekt sei, den elektrisch geladene Teilchen bei der Durchdringung von normaler Materie verursachen, wobei als Sekundärprozess Röntgenstrahlen erzeugt werden.[A 28] Er schrieb:
“It is a very interesting result of recent discoveries that the machinery which Le Sage introduced for the purpose of his theory has a very close analogy with things for which we have now direct experimental evidence […] Röntgen rays, however, when absorbed do not, as far as we know, give rise to more penetrating Rontgen rays as they should to explain attraction, but either to less penetrating rays or to rays of the same kind.”
„Es ist ein sehr interessantes Resultat jüngster Entdeckungen, dass die von Le Sage im Dienste seiner Theorie eingeführte Maschinerie eine sehr enge Analogie mit Dingen besitzt, für welche wir jetzt direkte experimentelle Gewissheit haben […] Röntgenstrahlen verursachen jedoch nicht die Entstehung von noch durchdringenderen Röntgenstrahlen, wie sie zur Erzeugung der Anziehung notwendig sind, sondern es entstehen gleiche oder weniger durchdringende Strahlen.“
- Tommasina, Brush
Im Gegensatz zu Lorentz und Thomson verwendete Thomas Tommasina um 1903[A 29] Wellen mit sehr großer Wellenlänge, kleine Wellenlängen benutzte er zur Erklärung chemischer Effekte. 1911[A 30] schlug Charles Francis Brush ebenfalls ein Modell mit Wellen großer Wellenlänge vor, jedoch änderte er später seine Meinung und zog Wellen mit extrem hoher Frequenz vor.
Weitere Einschätzungen
G. H. Darwin
1905 berechnete George Howard Darwin die Gravitationskraft zwischen zwei Körpern bei extrem geringen Abständen, um zu sehen, ob bei einem Le-Sage-Modell Abweichungen gegenüber dem Gravitationsgesetz auftreten. Er kam zu dem gleichen Schluss wie Lorentz, dass die Stöße völlig unelastisch sein müssen und im Gegensatz zur Annahme von Le Sage nicht nur bei senkrechter Einstrahlung, sondern auch bei Einstrahlung tangential zur Materieoberfläche. Dies geht einher mit einer Verschärfung der thermischen Problematik. Zusätzlich muss angenommen werden, dass alle elementaren Bestandteile der Materie von derselben Größe sind. Er führte weiter aus, dass die Emission von Licht und damit zusammenhängend der Strahlungsdruck eine genaue Entsprechung des Le Sage Modells darstelle. Ein Körper mit unterschiedlicher Oberflächentemperatur wird sich in Richtung des kälteren Teiles bewegen.[A 31] Später schließlich sagte er, dass er die Theorie ernsthaft in Betracht gezogen habe, aber er selbst werde sich nicht weiter mit ihr beschäftigen. Er glaubte nicht, dass irgendein Wissenschaftler sie als den richtigen Weg zu einer Erklärung der Gravitation akzeptiert.[A 32]
Poincaré

Teilweise auf den Berechnungen Darwins basierend, veröffentlichte Henri Poincaré 1908 eine ausführliche Kritik. Er folgerte, dass die Anziehung in einem solchen Modell proportional zu sei, wo S die Oberfläche aller Moleküle der Erde, v die Geschwindigkeit der Teilchen und ρ die Dichte des Mediums ist. Laplace folgend meinte er, dass um die Massenproportionalität zu wahren, die obere Grenze für S maximal der zehnmillionste Teil der Erdoberfläche ist. Er erklärte, dass der Widerstand proportional zu Sρv ist und somit das Verhältnis von Widerstand und Anziehung umgekehrt proportional zu Sv ist. Um den Widerstand im Verhältnis zu Anziehung möglichst gering zu halten, errechnete Poincaré als untere Grenze für die Geschwindigkeit der Teilchen den enormen Wert von v=24·1017·c aus, wobei c die Lichtgeschwindigkeit ist. Da jetzt untere Grenzen für Sv und v bekannt sind und auch eine obere Grenze für S feststeht, kann man daraus die Dichte und somit die Wärme berechnen, welche proportional zu Sρv3 ist. Diese reicht aus, um die Erde in jeder Sekunde um 1026 °C zu erhitzen. Poincaré vermerkte trocken, dass „die Erde einen solchen Zustand offenbar nicht lange ertragen würde“. Poincaré analysierte auch einige Wellenmodelle (Tommasina und Lorentz) und merkte an, dass diese dieselben Probleme wie die Teilchenmodelle haben (enorme Wellengeschwindigkeit, Erwärmung). Nach der Schilderung des auch von Thomson vorgeschlagenen Modells der Re-emission sekundärer Wellen, meinte Poincaré: „Zu solch komplizierten Hypothesen wird man genötigt, wenn man die Theorie von Le Sage gangbar machen will.“
Er fügte an, dass bei vollständiger Absorption im Rahmen des Modells von Lorentz die Erdtemperatur um 1013 °C pro Sekunde ansteigen würde. Poincaré untersuchte Le Sages Modell auch im Zusammenhang mit dem Relativitätsprinzip, wo die Lichtgeschwindigkeit eine unüberschreitbare Grenzgeschwindigkeit darstellt. Bei der Teilchentheorie merkte er deshalb an, dass es schwierig sei, ein mit dem neuen Relativitätsprinzip zu vereinbarendes Stoßgesetz aufzustellen.[A 33]
David Hilbert
1913 untersuchte David Hilbert in seinen Vorlesungen für Physik sowohl Le Sages und vor allem Lorentz’ Theorie. Er führte dabei an, dass dessen Theorie nicht funktioniere, da z. B. das Abstandsgesetz nicht mehr gültig sei, wenn der Abstand zwischen den Atomen groß genug im Vergleich zu ihrer Wellenlänge ist. Jedoch Erwin Madelung, ein Kollege Hilberts an der Universität Göttingen, benutzte das lorentzsche Schema zu Erklärung der molekularen Kräfte. Hilbert stufte Madelungs mathematisches Modell als sehr interessant ein, obwohl einige Aussagen nicht experimentell überprüfbar seien.[C 7]
Richard Feynman
1964 untersuchte Richard Feynman ebenfalls ein solches Modell, vor allem um herauszufinden, ob es möglich ist, einen Mechanismus für Gravitation ohne den Einsatz komplexer Mathematik zu finden. Jedoch nach Berechnung des Widerstandes, den die Körper in diesem Teilchenmeer erfahren müssen, gab er seine Bemühungen aus denselben Gründen auf (inakzeptable Geschwindigkeit), wie sie vorher geschildert wurden.[B 1] Er schloss:
‘Well’, you say, ‘it was a good one, and I got rid of the mathematics for awhile. Maybe I could invent a better one’. Maybe you can, because nobody knows the ultimate. But up to today, from the time of Newton, no one has invented another theoretical description of the mathematical machinery behind this law which does not either say the same thing over again, or make the mathematics harder, or predict some wrong phenomena. So there is no model of the theory of gravitation today, other than the mathematical form.
„›Gut‹, wirst du sagen, ›es war ein gutes Modell, und ich wurde die Mathematik für eine Weile los. Vielleicht könnte ich ein besseres Modell finden‹. Vielleicht kannst du das, weil niemand alles weiß. Aber von der Zeit Newtons bis jetzt hat keiner eine andere theoretische Beschreibung der mathematischen Maschinerie hinter diesem Gesetz gegeben, welche nicht entweder dieselbe Sache immer nur wiederholt, die Mathematik schwerer gemacht oder einige falsche Phänomene vorausgesagt hat. So gibt es bis heute kein anderes Modell der Gravitationstheorie als in der mathematischen Form.“
Voraussagen und Kritik
Materie und Teilchen
- Porosität der Materie
Eine grundlegende Vorhersage der Theorie ist die extreme Porosität der Materie. Wie bereits geschildert, muss Materie großteils aus leerem Raum bestehen, so dass die Teilchen nahezu ungehindert durchdringen können und so alle Bestandteile des Körpers gleichmäßig an der gravitativen Wechselwirkung teilnehmen. Diese Voraussage wurde (in gewisser Weise) im Laufe der Zeit bestätigt. Tatsächlich besteht Materie größtenteils aus leerem Raum (abgesehen von den Feldern) und bestimmte Teilchen wie Neutrinos können nahezu ungehindert durchdringen. Jedoch die Vorstellung der elementaren Bestandteile der Materie als klassische Entitäten, deren Wechselwirkungen durch direkten Kontakt erfolgen und abhängig sind von deren Form und Größe (zumindest wie das von Fatio bis Poincaré dargestellt wurde), entspricht nicht der Darstellung von Elementarteilchen in modernen Quantenfeldtheorien.
- Hintergrundstrahlung
Jedes Fatio/Le Sage Modell postuliert die Existenz eines den Raum erfüllenden, isotropen Fluids oder einer Strahlung von enormer Intensität und Durchdringungsfähigkeit. Dies hat einige Ähnlichkeit mit der Hintergrundstrahlung vor allem in Form des Mikrowellen-Hintergrundes (CMBR). Das CMBR ist tatsächlich eine den Raum erfüllende, isotrope Strahlung, jedoch ist ihre Intensität viel zu gering, genauso wie ihre Durchdringungsfähigkeit. Andererseits besitzen zwar Neutrinos die nötige Durchdringungsfähigkeit, jedoch ist diese Strahlung nicht isotrop (da einzelne Sterne die Hauptquellen der Neutrinos sind) und ihre Intensität ist noch geringer als die des CMBR. Zusätzlich breiten sich beide Strahlungsarten nicht mit Überlichtgeschwindigkeit aus, was zumindest nach obigen Berechnungen eine weitere Voraussetzung ist. Von einem modernen Standpunkt aus, und nicht im Zusammenhang mit Fatios Modell, wurde die Möglichkeit von Neutrinos als Überträgerteilchen in einer Quantengravitation von Feynman in Betracht gezogen und widerlegt.[B 2]
Abschirmung

Dieser Effekt hängt eng mit der vorausgesetzten Porosität und Durchdringbarkeit der Materie zusammen, welche notwendig ist, um die Proportionalität zur Masse aufrechtzuerhalten. Um das genauer auszuführen: Diejenigen Atome, welche nicht mehr von den Teilchen getroffen werden, würden keinen Anteil an der Abschirmung und somit der schweren Masse des Körpers mehr haben (B10, oben). Dieser Effekt kann jedoch durch entsprechende Erhöhung der Porosität der Materie, d. h. durch die Verkleinerung ihrer Bestandteile, beliebig minimiert werden. Somit wird die Wahrscheinlichkeit, dass diese Bestandteile genau auf einer Linie liegen und sich gegenseitig abschirmen, reduziert (B10, unten). Ganz lässt sich dieser Effekt jedoch nicht ausschalten, denn um eine vollständige Durchdringbarkeit zu erreichen, dürften die Bestandteile der Materie überhaupt nicht mehr mit den Teilchen wechselwirken, was aber auch das Verschwinden jeglicher Gravitation zur Folge hätte. Das bedeutet, ab einer bestimmten Grenze müsste eine Differenz zwischen träger und schwerer Masse, also eine Abweichung vom Äquivalenzprinzip, zu beobachten sein.
Jegliche Abschirmung der Gravitation ist also eine Verletzung des Äquivalenzprinzips und folglich unvereinbar mit dem Gravitationsgesetz Newtons als auch der Allgemeinen Relativitätstheorie (ART) Einsteins. Bislang wurde jedoch keine Abschirmung der Gravitation beobachtet.[C 8] Für mehr Informationen über den Zusammenhang Le Sage und Abschirmung der Gravitation, siehe Martins.[C 9][C 10]
Bezüglich Isenkrahes Vorschlag einer Verbindung zwischen Dichte, Temperatur und Gewichtskraft: Da seine Argumentation auf der Änderung der Dichte beruht, und die Temperatur bei konstanter Dichte gesenkt und erhöht werden kann, impliziert Isenkrahes Theorie keinen grundlegenden Zusammenhang zwischen Temperatur und Gewicht. (Es existiert zwar tatsächlich ein solcher Zusammenhang, jedoch nicht im Sinne von Isenkrahe. Siehe Abschnitt Wechselwirkung mit Energie). Auch die Voraussage einer Beziehung zwischen Dichte und Gewichtskraft konnte experimentell nicht bestätigt werden.
Geschwindigkeit
- Widerstand
Eines der Hauptprobleme der Theorie ist, dass ein Körper, der sich relativ zu dem Bezugssystem bewegt, in dem die Geschwindigkeit der Teilchen in alle Richtungen gleich ist, einen Widerstand in Bewegungsrichtung spüren müsste. Das liegt daran, dass die Geschwindigkeit der auf den Körper auftreffenden Teilchen in Bewegungsrichtung größer ist. Analog dazu ist der Doppler-Effekt bei Wellenmodellen zu beachten. Dieser Widerstand führt zu einer stetigen Verkleinerung der Umlaufbahn um die Sonne und ist (nach Fatio, Le Sage und Poincaré) proportional zu uv, wo u die Geschwindigkeit des Körpers und v die der Teilchen ist. Andererseits ist die Gravitationskraft proportional zu v², woraus sich ergibt, dass das Verhältnis von Widerstand zur Gravitationskraft proportional zu u/v ist. Bei einer bestimmten Geschwindigkeit u kann der effektive Widerstand also durch Erhöhung von v beliebig klein gemacht werden. Wie von Poincaré errechnet, muss v mindestens 24·1017·c betragen, also sehr viel größer als die Lichtgeschwindigkeit sein. Das macht die Theorie unvereinbar mit der Mechanik der Speziellen Relativitätstheorie, in welcher keine Teilchen (oder Wellen) sich schneller als Licht ausbreiten können, denn aufgrund der Relativität der Gleichzeitigkeit käme es je nach Bezugssystem zu Kausalitätsverletzungen. Selbst wenn superluminale Geschwindigkeiten möglich wären, würde das wieder zu einer enormen Wärmeproduktion führen – siehe unten.
- Aberration
Ein ebenfalls von der Teilchengeschwindigkeit abhängiger Effekt ist die Aberration der Gravitation. Aufgrund der endlichen Geschwindigkeit der Gravitation kommt es zu Zeitverzögerungen bei der Wechselwirkung der Himmelskörper, welche im Gegensatz zum Widerstand zu einer stetigen Vergrößerung der Umlaufbahnen führen. Auch hier muss eine größere Geschwindigkeit als die des Lichts angenommen werden. Während Laplace noch eine untere Grenze von 107·c angab, ergaben neuere Beobachtungen eine untere Grenze von 1010·c.[B 3] Es ist nicht bekannt, ob im Le-Sage-Modell ebenfalls Effekte wie in der ART auftreten, welche diese Form der Aberration kompensieren.
Reichweite
Die Schattenwirkung gilt nur dann exakt nach 1/r², wenn keine Wechselwirkung der Teilchen untereinander auftritt – d. h., das Abstandsgesetz ist abhängig von der mittleren freien Weglänge der Teilchen. Kollidieren sie jedoch miteinander, „verwischt“ sich der Schatten bei größerer Entfernung. Dieser Effekt ist abhängig von dem jeweils vertretenen Modell und den dabei angenommenen internen Energiemodi der Teilchen oder Wellen. Um diesem Problem generell auszuweichen, postulierten Kelvin und andere, dass die Teilchen jederzeit beliebig klein definiert werden könnten, wodurch sie sich trotz großer Anzahl nur sehr selten begegnen würden – dadurch wäre dieser Effekt minimiert. Das Vorhandensein von großräumigen Strukturen im Universum wie Galaxienhaufen spricht jedenfalls für eine Reichweite der Gravitation über zumindest mehrere Millionen Lichtjahre hinweg.
Energie
- Absorption
Wie in dem historischen Abschnitt erklärt, ist ein weiteres Problem dieses Modells die Absorption von Energie und somit die Produktion von Wärme. Aronson gab dafür ein einfaches Beispiel:[C 11]
- Ist die kinetische Energie der Teilchen kleiner als die der Körper, werden sich die Teilchen nach den Kollisionen mit größerer Geschwindigkeit bewegen und die Körper werden sich abstoßen.
- Sind Körper und Teilchen im thermischen Gleichgewicht, entsteht keine Kraft.
- Ist die kinetische Energie der Körper kleiner als die der Teilchen, entsteht eine anziehende Kraft. Aber wie von Maxwell und Poincaré gezeigt, müssten diese unelastische Kollisionen die Körper in Sekundenbruchteilen zur Weißglut bringen, vor allem wenn eine Teilchengeschwindigkeit größer als c angenommen wird.
Isenkrahes bewusste Verletzung des Energieerhaltungssatzes als Lösungsmöglichkeit war genauso unakzeptabel wie Kelvins Anwendung des Theorems von Clausius, was, wie Kelvin selbst bemerkt hat, zu einem Perpetuum-mobile-Mechanismus führt. Der Vorschlag eines sekundären Re-Emissionsmechanismus für Wellenmodelle (analog zu Kelvins Veränderung der Energiemodi) erregte das Interesse von J. J. Thomson, wurde jedoch von Maxwell und Poincaré nicht sonderlich ernst genommen. Dabei würden nämlich große Mengen an Energie spontan von einer kalten in eine wärmere Form konvertiert, was eine grobe Verletzung des zweiten Hauptsatzes der Thermodynamik darstellt.
Das Energieproblem wurde ebenfalls im Zusammenhang mit der Idee einer Massenzunahme und der Expansionstheorie erörtert. Iwan Ossipowitsch Jarkowski 1888 und Ott Christoph Hilgenberg 1933 kombinierten ihre Expansionsmodelle mit der Absorption eines Äthers.[C 12] Diese Theorie wird jedoch weitgehend nicht mehr als gültige Alternative zur Plattentektonik angesehen. Darüber hinaus würde aufgrund der Äquivalenz von Masse und Energie und der Anwendung der von Poincaré errechneten Energieabsorptionswerte der Erdradius in kürzester Zeit beträchtlich zunehmen.
- Wechselwirkung
Wie in der ART vorhergesagt und basierend auf experimentellen Bestätigungen, wechselwirkt Gravitation mit jeder Form von Energie und nicht nur mit normaler Materie. Die elektrostatische Bindungsenergie der Nukleonen, die Energie der schwachen Wechselwirkung der Nukleonen und die kinetische Energie der Elektronen tragen alle zur schweren Masse eines Atoms bei, wie in Hochpräzisionsmessungen vom Eötvös-Typ nachgewiesen wurde.[B 4] Das bedeutet, dass eine schnellere Bewegung der Gasteilchen eine Erhöhung der Gravitationswirkung des Gases bewirkt. Le Sages Theorie sagt ein solches Phänomen nicht voraus, noch tun das die anderen bekannten Variationen der Theorie.
Nicht-gravitative Anwendungen und Analogien
- Mock gravity
Lyman Spitzer errechnete 1941[B 5], dass Absorption von Strahlung zwischen zwei Staubpartikeln zu einer scheinbaren Anziehungskraft führt, welche proportional zu 1/r² ist (wobei ihm offensichtlich die analogen Theorien von Le Sage und insbesondere die Untersuchungen von Lorentz zum Strahlungsdruck unbekannt waren). George Gamow, der diesen Effekt als mock gravity bezeichnete, schlug 1949[B 6] vor, dass nach dem Urknall die Temperatur der Elektronen schneller gesunken sei als die Temperatur der Hintergrundstrahlung. Absorption der Strahlung führe zu dem von Spitzer errechneten Le-Sage-Mechanismus zwischen den Elektronen, welcher eine wichtige Rolle bei der Galaxienbildung nach dem Urknall gespielt haben soll. Jedoch wurde dieser Vorschlag 1971 von Field[B 7] widerlegt, der zeigte, dass dieser Effekt viel zu klein gewesen ist, da die Elektronen und die Strahlung sich annähernd im thermischen Gleichgewicht befunden haben. Hogan und White schlugen 1986[B 8] vor, dass eine Form von mock gravity die Galaxienbildung durch Absorption vorgalaktischen Sternenlichtes beeinflusst hat. Aber 1989[B 9] zeigten Wang und Field, dass jede Form von Mock gravity nicht in der Lage ist, eine ausreichend große Wirkung zustande zu bringen, um die Galaxienformation zu beeinflussen.
- Plasma
Der Le-Sage-Mechanismus wurde als signifikanter Faktor im Verhalten komplexer Plasmen[B 10] identifiziert. Ignatov zeigte, dass durch unelastische Kollisionen eine anziehende Kraft zwischen zwei in einem kollisionsfreien, nichtthermischen Plasma suspendierten Staubkörnern entsteht. Diese Anziehungskraft ist umgekehrt proportional zum Quadrat der Entfernung zwischen den Staubkörnern und kann die Coulomb-Abstoßung zwischen ihnen ausgleichen.[B 11]
- Vakuumenergie
In der Quantenfeldtheorie wird die Existenz von virtuellen Teilchen angenommen, welche zum so genannten Casimir-Effekt führen. Hendrik Casimir fand heraus, dass bei der Berechnung der Vakuumenergie zwischen 2 Platten nur Teilchen von bestimmten Wellenlängen auftreten. Deswegen ist die Energiedichte zwischen den Platten geringer als außerhalb, was zu einer scheinbaren Anziehungskraft zwischen den Platten führt. Dieser Effekt hat jedoch eine von der Theorie Fatios sehr verschiedene theoretische Grundlage.
Neuere Entwicklungen
Die Untersuchung von Le Sages Theorie im 19. Jahrhundert identifizierte mehrere eng zusammenhängende Probleme. Dazu zählen die enorme Erwärmung, instabile Umlaufbahnen durch Widerstand und Aberration sowie die nicht beobachtete Abschirmung der Gravitation. Die Erkenntnis dieser Probleme zusammen mit einer generellen Abkehr von kinetischen Gravitationsmodellen resultierte in einem zunehmenden Verlust an Interesse. Schließlich wurden Le Sages und andere Theorien durch Einsteins Allgemeine Relativitätstheorie verdrängt.
Obwohl das Modell nicht mehr als gültige Alternative angesehen wird, werden außerhalb des Mainstreams Versuche zu einer Revitalisierung unternommen, wie die Modelle von Radzievskii und Kagalnikova (1960),[B 12] Shneiderov (1961),[B 13] Buonomano and Engels (1976),[B 14] Adamut (1982),[B 15] Jaakkola (1996),[B 16] Van Flandern (1999)[B 17] und Edwards (2007).[B 18] Verschiedene Le-Sage-Modelle und verwandte Themen werden in Edwards et al. diskutiert.[B 19]
Ein Arbeitspapier über eine neuartige, nicht verifizierte, quantitative Push-Gravitationstheorie von Danilatos (2020), wurde auf der nicht referierten Zenodo-Plattform des CERN veröffentlicht.[B 20]
Literatur
Historische Primärquellen
- Bock, Adalbert M.: Die Theorie der Gravitation von Isenkrahe in ihrer Anwendung auf die Anziehung und Bewegung der Himmelskörper. Dissertation. München 1891.
- Boisbaudran, Lecoq de: Note sur la théorie de la pesanteur. In: Comptes Rendus. Band 69, 1869, S. 703–705 (Online).
- Du Bois-Reymond, Paul: Ueber die Unbegreiflichkeit der Fernkraft. In: Naturwissenschaftliche Rundschau. Band 3, Nr. 14, 1888, S. 169–176 (Online).
- Brush, Charles Francis: A kinetic theory of gravitation. In: Nature. Band 86, 1911, S. 130–132.
- G. Cramer: Theses Physico-Mathematicae de Gravitate (Dissertation). Genf 1731.
- Darwin, George Howard: The analogy between Lesage’s theory of gravitation and the repulsion of light. In: Proc. Royal Soc. Band 76, 1905, S. 387–410 (Online).
- Darwin, George Howard: Introduction to Dynamical Astronomy. 1916.
- Fatio de Duillier, Nicolas: Lettre N° 2570. In: Société Hollandaise des Sciences (Hrsg.): Oeuvres complètes de Christiaan Huygens. Band 9. Den Haag 1690, S. 381–389 (Online).
- Fatio de Duillier, Nicolas: Drei Untersuchungen zur Geschichte der Mathematik, in: Schriften der Straßburger Wissenschaftlichen Gesellschaft in Heidelberg. Hrsg.: Karl Bopp. Band 10. Berlin & Leipzig 1929, Die wiederaufgefundene Abhandlung von Fatio de Duillier: De la cause de la Pesanteur, S. 19–66.
- Fatio de Duillier, Nicolas: De la Cause de la Pesanteur: Mémoire de Nicolas Fatio de Duillier. In: Notes and Records of the Royal Society of London. Band 6, 1. Mai 1949, S. 125–160, doi:10.1098/rsnr.1949.0018 (Online).
- Isenkrahe, Caspar: Das Räthsel von der Schwerkraft: Kritik der bisherigen Lösungen des Gravitationsproblems und Versuch einer neuen auf rein mechanischer Grundlage. Friedrich Vieweg und Sohn, Braunschweig 1879.
- Jarolimek, A.: Über die Gravitation. In: Wien. Ber. Band 88, 1883, S. 897–911.
- Kant, Immanuel: Metaphysische Anfangsgründe der Naturwissenschaft: Dynamik, Lehrsatz 5. In: . 1786 (Online).
- Keller, F. A. E. & Keller, É.: Mémoire sur la cause de la pesanteur et des effets attribués à l’attraction universelle. In: Comptes Rendus. Band 56, 1863, S. 530–533 (Online).
- Laplace, Pierre-Simon: A Treatise in Celestial Mechanics. 4, Buch 10. Chelsea (New York) 1966, Kapitel 7.
- Leray, P.: Theorie nouvelle de la gravitation. In: Comptes Rendus. Band 69, 1869, S. 615–621 (Online).
- Le Sage, Georges-Louis: Letter à une académicien de Dijon … In: Mercure de France. 1756, S. 153–171.
- Le Sage, Georges-Louis: Essai de Chymie Méchanique. In: . Privatdruck, Genf 1761 (Online).
- Le Sage, Georges-Louis: Lucrèce Newtonien. In: Memoires de l’Academie Royale des Sciences et Belles Lettres de Berlin. 1784, S. 404–432 (Online). Englische Übersetzung: Georges-Louis Le Sage: The Newtonian Lucretius. In: Annual Report of the Board of Regents of the Smithsonian Institution. 1898, S. 139–160.
- Le Sage, Georges-Louis: Deux Traites de Physique Mécanique. Hrsg.: P. Prévost. J. J. Paschoud, Genf/Paris 1818, Physique Mécanique des Georges-Louis Le Sage, S. 1–186.
- Lichtenberg, Georg Christoph: Nachrichten der Akademie der Wissenschaften zu Göttingen, II. mathematisch-physikalische Klasse. Hrsg.: Horst Zehe, Wiard Hinrichs. Band 1. Vandenhoeck & Ruprecht, Göttingen 2003, Ist es ein Traum, so ist es der größte und erhabenste der je ist geträumt worden ….
- Lorentz, Hendrik: Considerations on Gravitation. In: Proc. Acad. Amsterdam. Band 2, 1900, S. 559–574.
- Lorentz, Hendrik: Lectures On Theoretical Physics. Macmillan and Co., London 1922 (Online).
- Maxwell, James Clerk: Atom. In: Encyclopedia Britannica. Band 3, 1875, S. 38–47.
- Poincaré, Henri: La dynamique de l’électron. In: Revue générale des sciences pures et appliquées. Band 19, 1908, S. 386–402 (Online [PDF]). Deutsche Übersetzung in: Poincaré, Henri: Wissenschaft und Methode. Xenomos, Berlin 2003, ISBN 3-936532-31-1.
- Preston, Samuel Tolver: On some dynamical conditions applicable to LeSage’s theory of gravitation. In: Phil. Mag., fifth ser. Band 4, Nr. 24, 1877, S. 206–213, doi:10.1080/14786447708639322.
- Preston, Samuel Tolver: On some dynamical conditions applicable to LeSage’s theory of gravitation. In: Phil. Mag., fifth ser. Band 4, Nr. 26, 1877, S. 364–375, doi:10.1080/14786447708639355.
- Redeker, Franz Albert: De causa gravitatis meditatio. In: Lemgoviae ex officina Meyeriana. 1736.
- Rysánek, Adalbert: Versuch einer dynamischen Erklärung der Gravitation. In: Repertorium der Physik. Band 24, 1887, S. 90–115.
- Schelling, Friedrich Wilhelm Joseph: Ideen zu einer Philosophie der Natur. 1797, Einige Bemerkungen über die mechanische Physik des Herrn le Sage, S. 296–308.
- Tait, Peter Guthrie: Lectures on some recent advances in physical science with a special lecture on force. Macmillan and Co., London 1876 (Online).
- Tommasina, Thomas: La Physique de la Gravitation. Gauthier-Villars, Paris 1928.
- Thomson, William (Lord Kelvin): On the ultramundane corpuscles of Le Sage. In: Phil. Mag. Band 45, 1873, S. 321–332 (Online).
- Thomson, J. J.: Electricity and matter. Archibald Constable & Co., Ltd., Westminster 1904 (Online).
- Thomson, J. J.: Matter. In: Encyclopædia Britannica. 1911, S. 891–895.
- Einzelnachweise zur historischen Primärliteratur
- ↑ Fatio (1690)
- ↑ Fatio (1701)
- ↑ Fatio (1743)
- ↑ Cramer (1731)
- ↑ Redeker (1736)
- ↑ Le Sage (1756)
- ↑ Le Sage (1761)
- ↑ Le Sage (1782)
- ↑ Le Sage (1818)
- ↑ Lichtenberg (2003)
- ↑ Kant (1786)
- ↑ Schelling (1797)
- ↑ Laplace (1805)
- ↑ Leray (1869)
- ↑ Thomson (1873)
- ↑ a b Tait (1876)
- ↑ Preston (1877)
- ↑ a b c Maxwell (1875)
- ↑ Isenkrahe (1879)
- ↑ Bock (1891)
- ↑ Rysanek (1887)
- ↑ Bois-Reymond (1888)
- ↑ Keller (1863)
- ↑ Boisbaudran (1869)
- ↑ Lorentz (1900)
- ↑ Lorentz (1922)
- ↑ Thomson (1911)
- ↑ a b Thomson (1911)
- ↑ Tommasina (1928)
- ↑ Brush (1911)
- ↑ Darwin (1905)
- ↑ Darwin (1916)
- ↑ Poincaré (1908)
Primärquellen
- Adâmuți, I. A.: The screen effect of the earth in the TETG. Theory of a screening experiment of a sample body at the equator using the earth as a screen. In: Nuovo Cimento C. Band 5, Nr. 2, 1982, S. 189–208, doi:10.1007/BF02509010.
- Buonomano, V. & Engel, E.: Some speculations on a causal unification of relativity, gravitation, and quantum mechanics. In: Int. J. Theor. Phys. Band 15, Nr. 3, 1976, S. 231–246, doi:10.1007/BF01807095.
- Carlip, Steve: Kinetic Energy and the Equivalence Principle. In: Am. J. Phys. Band 66, Nr. 5, 1997, S. 409–413, doi:10.1119/1.18885, arxiv:gr-qc/9909014.
- Carlip, Steve: Aberration and the Speed of Gravity. In: Phys. Lett. A. Band 167, Nr. 2–3, 1999, S. 81–87, doi:10.1016/S0375-9601(00)00101-8, arxiv:gr-qc/9909087.
- Edwards, M. R. (Hrsg.): Pushing Gravity: New Perspectives on Le Sage's Theory of Gravitation. C. Roy Keys Inc., Montreal 2002, ISBN 0-9683689-7-2.
- Edwards, M.R.: Photon-Graviton Recycling as Cause of Gravitation. In: Apeiron. Band 14, Nr. 3, 2007, S. 214–233 (Online [PDF]).
- Feynman, R. P.: The Character of Physical Law, The 1964 Messenger Lectures. 1967, S. 37–39.
- Feynman, R. P.: Feynman Lectures on Gravitation. Addison-Wesley, Reading 1995, S. 23–28.
- Field, G. B.: Instability and waves driven by radiation in interstellar space and in cosmological models. In: The Astrophysical Journal. Band 165, 1971, S. 29–40, bibcode:1971ApJ...165...29F.
- Field, G.B. & Wang, B.: Galaxy formation by mock gravity with dust? In: The Astrophysical Journal. Band 346, 1989, S. 3–11, bibcode:1989ApJ...346....3W.
- Gamow, George: On relativistic cosmogony. In: Reviews of modern physics. Band 21, Nr. 3, 1949, S. 367–373, doi:10.1103/RevModPhys.21.367 (Online).
- Hogan, C.J.: Mock gravity and cosmic structure. In: The Astrophysical Journal. Band 340, 1989, S. 1–10, bibcode:1989ApJ...340....1H.
- Ignatov, A.M.: Lesage gravity in dusty plasma. In: Plasma Physics Reports. Band 22, Nr. 7, 1996, S. 585–589.
- Jaakkola, T.: Action-at-a-distance and local action in gravitation: discussion and possible solution of the dilemma. In: Apeiron. Band 3, 1996, S. 61–75 (Online [PDF]).
- Radzievskii, V.V. & Kagalnikova, I.I.: The nature of gravitation. In: Vsesoyuz. Astronom.-Geodezich. Obsch. Byull. Band 26, Nr. 33, 1960, S. 3–14. Englische Übersetzung: U.S. government technical report: FTD TT64 323; TT 64 11801 (1964), Foreign Tech. Div., Air Force Systems Command, Wright-Patterson AFB, Ohio.
- Shneiderov, A. J.: On the internal temperature of the earth. In: Bollettino di Geofisica Teorica ed Applicata. Band 3, 1961, S. 137–159.
- Spitzer, L.: The dynamics of the interstellar medium; II. Radiation pressure. In: The Astrophysical Journal. Band 94, 1941, S. 232–244, bibcode:1941ApJ....94..232S.
- Van Flandern, Tom: Dark Matter, Missing Planets and New Comets. North Atlantic Books, Berkeley 1999, S. Chapters 2–4.
- Danilatos, Gerasimos: Novel quantitative push gravity theory poised for verification. In: Zenodo. 2020 (Online).
- Einzelnachweise zur Primärliteratur
- ↑ Feynman (1964)
- ↑ Feynman (1995)
- ↑ Carlip (1999)
- ↑ Carlip (1997)
- ↑ Spitzer (1941)
- ↑ Gamow (1949)
- ↑ Field (1971)
- ↑ Hogan (1989)
- ↑ Field (1989)
- ↑ Siehe Carsten Killer: Staubige Plasmen - eine Einführung. August 2016, archiviert vom (nicht mehr online verfügbar) am 21. Februar 2018; abgerufen am 21. Februar 2018.
- ↑ Ignatov (1996)
- ↑ Radzievskii (1960)
- ↑ Shneiderov (1961)
- ↑ Buonomano (1976)
- ↑ Adamut (1982)
- ↑ Jaakkola (1996)
- ↑ Van Flandern (1999)
- ↑ Edwards (2007)
- ↑ Edwards (2002)
- ↑ Danilatos (2020)
Sekundärquellen
- Aronson, S.: The gravitational theory of Georges-Louis Le Sage. In: The Natural Philosopher. Band 3, 1964, S. 51–74.
- Bertolami, O. & Paramos, J. & Turyshev, S. G.: General Theory of Relativity: Will it survive the next decade? In: Lasers, Clocks, and Drag-Free: Technologies for Future Exploration in Space and Tests of Gravity. 2006, S. 27–67, arxiv:gr-qc/0602016v2.
- Chabot, H.: Nombre et approximations dans la théorie de la gravitation de Lesage. In: Actes des Journées de Peirescq "La pensée numérique", Sciences et Techniques en Perspective, 2ème série. Band 8, 2004, S. 179–198 (Online [PDF]).
- Corry, L.: David Hilbert between Mechanical and Electromagnetic Reductionism. In: Archive for History of Exact Sciences. Band 53, Nr. 6, 1999, S. 489–527 (Online [PDF]).
- Drude, Paul: Ueber Fernewirkungen. In: Beilage zu den Annalen der Physik und Chemie. Band 298, Nr. 12, 1897, S. I-XLIX, doi:10.1002/andp.18972981220.
- Evans, J. C.: Pushing Gravity: New Perspectives on Le Sage's Theory of Gravitation. Hrsg.: Edwards, M.R. C. Roy Keys Inc., Montreal 2002, Gravity in the century of light: sources, construction and reception of Le Sage's theory of gravitation, S. 9–40.
- Isenkrahe, Caspar: Über die Rückführung der Schwere auf Absorption und die daraus abgeleiteten Gesetze. In: Abhandlungen zur Geschichte der Mathematik. Band 6. Leipzig 1892, S. 161–204 (Online).
- Martins, de Andrade, R.: The Expanding Worlds of General Relativity (Einstein Studies). Hrsg.: Goemmer, H., Renn, J., and Ritter, J. Band 7. Birkhäuser, Boston 1999, The search for gravitational absorption in the early 20th century, S. 3–44.
- Martins, de Andrade, R.: Pushing Gravity: New Perspectives on Le Sage's Theory of Gravitation. Hrsg.: Edwards, M.R. C. Roy Keys Inc., Montreal 2002, Gravitational absorption according to the hypotheses of Le Sage and Majorana, S. 239–258.
- Playfair, J.: Notice de la Vie et des Ecrits de George Louis Le Sage. In: Edinburgh Review. 1807, S. 137–153.
- Prevost, Pierre (Hrsg.): Notice de la Vie et des Ecrits de George Louis Le Sage. J. J. Paschoud, Geneva & Paris 1805 (Online).
- Rowlinson, J. S.: Le Sage's Essai de Chymie Méchanique. In: Notes Rec. R. Soc. London. Band 57, 2003, S. 35–45, doi:10.1098/rsnr.2003.0195, JSTOR:3557680.
- Scalera, G. and Jacob, K.-H. (Hrsg.): Why expanding Earth? – A book in honour of O.C. Hilgenberg. INGV, Rome 2003.
- Taylor, W. B.: Kinetic Theories of Gravitation. In: Smithsonian report. 1876, S. 205–282.
- Wolf, R.: George-Louis Le Sage. In: Biographien zur Kulturgeschichte der Schweiz. Band 4, 1862, S. 173–192 (Google Books).
- Zehe, H.: Die Gravitationstheorie des Nicolas Fatio de Duillier. Gerstenberg Verlag, Hildesheim 1980, ISBN 3-8067-0862-2.
- Zenneck, Jonathan: Gravitation. In: Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. Band 5, Nr. 1. B.G. Teubner, Leipzig 1903, S. 25–67 (Online).
- Einzelnachweise zur Sekundärliteratur
- ↑ a b Prevost (1805)
- ↑ a b c d e Zehe (1980)
- ↑ Wolf (1862)
- ↑ Evans (2002)
- ↑ a b Playfair (1807)
- ↑ Drude (1897)
- ↑ Corry (1999)
- ↑ Bertolami (2006)
- ↑ Martins (1999)
- ↑ Martins (2002)
- ↑ Aronson (1964)
- ↑ Scalera (2003)
















