Kapillareffekt


Der Kapillareffekt, auch Kapillarwirkung, ist ein Phänomen in der Physik flüssiger Materie. Kapillarität ist in erster Linie die Stoffeigenschaft, die den Effekt hervorruft, wird aber auch synonym zu Kapillareffekt verwendet. Durch die vom Kapillareffekt hervorgerufene Kapillarkraft bewegt sich die Grenzfläche in Abwesenheit treibender externer Kräfte oder sogar entgegen zu externen Kräften, wie etwa der Gravitationskraft.
Der Effekt tritt auf, wenn sich die Grenzfläche (ein sog. Meniskus) einer Flüssigkeit in einer Kapillaren oder Spalten eines Feststoffs befindet. Die Grenzfläche liegt dabei zwischen einer Flüssigkeit und einer zweiten fluiden Phase, wie einem Gas oder einer weiteren Flüssigkeit, die mit der ersten Flüssigkeit nicht mischbar ist. Der Kapillareffekt wird durch die Oberflächenspannung der Flüssigkeit (Kohäsion) und die Grenzflächenspannung zwischen der Flüssigkeit und der festen Oberfläche (Adhäsion) beziehungsweise die Benetzbarkeit der festen Oberfläche mit der Flüssigkeit bestimmt.[1]
Da das Gewicht der Flüssigkeit in engen Hohlräumen gering ist, überwiegt die Kapillarkraft gegenüber der Schwerkraft und hilft etwa Bäumen dabei, Wasser aus den Wurzeln bis zu 100 Meter hoch aufsteigen zu lassen (siehe Wassertransport in Pflanzen). Die Kapillarität des Dochts bewirkt, dass flüssiges Wachs im Docht zur Flamme aufsteigt und dass sich poröse Materialien wie Ziegel, Textilien und Papier mit Wasser vollsaugen. In nicht-porösem Material steigt Wasser gegen die Gravitationskraft auf, wenn feine Spalte vorliegen wie etwa in feinem Sand oder engen Glasröhrchen.
Effekte
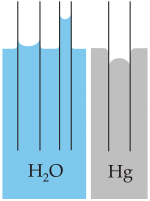
Kapillaraszension (Kapillarer Aufstieg) tritt bei Flüssigkeiten auf, die das Material des Kapillargefäßes benetzen, wie beispielsweise Wasser auf Glas oder auf Papierfasern. Das Wasser steigt in einem Glasröhrchen auf und bildet eine konkave Oberfläche (Meniskus). Dieses Verhalten ist auf die Adhäsionskraft zwischen dem Wasser und dem Glas zurückzuführen.
Kapillardepression (Kapillarer Abstieg) tritt auf, wenn die Flüssigkeit das Material der Gefäßoberfläche nicht benetzt. Beispiele dafür sind Quecksilber auf Glas oder Wasser auf einer fettigen Oberfläche. Solche Flüssigkeiten haben in einem Röhrchen einen niedrigeren Pegel als in der Umgebung und bilden eine konvex geformte Oberfläche.
Bis zu einem gewissen Mindestdurchmesser gilt, dass je kleiner der Durchmesser der Kapillaren, desto größer sind der Kapillardruck und die Steighöhe, siehe Formel und Tabelle unten.
Weiche poröse Materialien wie Schwämme und Wischtücher haben ein großes Saugvermögen, solange ihre Struktur dem Kapillarsog standhält und nicht zusammenfällt.
In einem an beiden Seiten offenen Röhrchen steigt die Flüssigkeit aufgrund von Adhäsionskräften an der Wandung des Röhrchens genau bis zu dessen Ende auf, selbst wenn die Kapillarität eine größere Steighöhe erlaubte.
In der Medizin und chemischen Analytik werden Glaskapillaren bzw. Kapillarpipetten zur Entnahme, Abmessung und Dosierung kleiner Flüssigkeitsmengen verwendet. Durch die Kapillarwirkung kann die Aufnahme selbsttätig geschehen.
Ein Gefäß kann sich restlos entleeren, wenn ein Lappen zu beiden Seiten des Rands herunterhängt. Die Flüssigkeit steigt durch Kapillarkraft im Textil auf, tritt über den Rand und verteilt sich im gesamten Lappen. Die Flüssigkeit außerhalb des Gefäßes wird durch die Schwerkraft nach unten gezogen und saugt die Flüssigkeit im Gefäß über die Heberwirkung in den Kapillaren nach, solange sich der außerhalb herabhängende Rand des Textils unterhalb des Flüssigkeitsspiegels im Gefäß befindet.
Eine grobkörnige, kapillarbrechende Schicht verhindert aufsteigende Nässe in Bauwerken und wird auch als Frostschutzschicht unter Straßendecken eingebaut.
Molekulare Betrachtung
Grundsätzlich beruht der Effekt der Kapillarität auf den Molekularkräften, die innerhalb eines Stoffes (Kohäsionskräfte) und an der Grenzfläche zwischen einer Flüssigkeit, einem festen Körper (Gefäßwand) und einem Gas (z. B. Luft) auftreten (Adhäsionskräfte). Häufig hat der Kapillareffekt auch die Bedeutung von Oberflächenspannung.
Im Innern eines Körpers heben sich die auf ein bestimmtes Molekül wirkenden Kräfte aus seiner Umgebung gegenseitig auf. An den Rändern jedoch ergibt sich eine resultierende Kraft, die in Abhängigkeit vom jeweiligen Material entweder in die Flüssigkeit hinein oder aus ihr heraus gerichtet ist. Ist die Wirkung der Gefäßwandung gegenüber den Kohäsionskräften in der Flüssigkeit klein, dann zeigt die resultierende Kraft ins Innere der Flüssigkeit. Deren Oberfläche ist an der Kontaktstelle zur Wand nach unten gekrümmt und benetzt die Gefäßwand nicht (z. B. Quecksilber im Glasgefäß). Ist jedoch die Wirkung der Gefäßwandung gegenüber den Kohäsionskräften in der Flüssigkeit groß, dann zeigt die resultierende Kraft in die Gefäßwandung hinein, und die Flüssigkeit ist am Rande nach oben gebogen. Die Flüssigkeit benetzt die Wandung (z. B. Wasser oder Petroleum im Glasgefäß).
Praktische Anwendungen
Füller: Ein Beispiel für eine Anwendung ist der Füller oder Füllfederhalter: Dessen Tintenleiter speichert Tinte und ersetzt die an der Federspitze verbrauchte Tinte mittels Kapillarkräften. Dabei wird Tinte aus einem Reservoir nachgefördert und zugleich die Belüftung dieses Reservoirs ermöglicht. Auch Schreibfedern speichern Tinte mittels Kapillarkräften, entweder in einem Loch oder in einem Spalt zwischen der eigentlichen Feder und einer Überfeder, um von dort durch die Kapillarwirkung durch einen sehr feinen Schlitz an die Spitze transportiert zu werden.

Papier: Papier saugt durch den Kapillareffekt die Tinte auf; es ist sogar möglich, über Kopf zu schreiben. Auf glatten Oberflächen wie etwa Glas ist Schreiben mit einem Füller kaum möglich, da die Tinte die Glasoberfläche nur oberflächlich benetzt, aber nicht aufgenommen wird.
Pflanzen: In Bäumen und anderen Pflanzen wird das Wasser von den Wurzeln aufgenommen und dann bis in die Krone transportiert, wo es aus den Spaltöffnungen der Blätter (oder Nadeln) verdunstet oder für die Photosynthese benötigt wird. Die Verdunstung im oberen Bereich der Pflanze bewirkt einen Transpirationssog, Kohäsionskräfte des Wassers in der Pflanze verhindern ein Abreißen des Flüssigkeitsstroms, und der Kapillareffekt begünstigt mit dem osmotischen Effekt (Wurzeldruck) den Aufstieg.[2] Nach neuen Erkenntnissen können Bäume maximal 130 Meter hoch werden, da dann der osmotische Druck zusammen mit den Kapillarkräften nicht mehr ausreicht, die Schwerkraft zu überwinden.[3] Siehe Wassertransport in Pflanzen
Chemie: In der Papierchromatographie nutzt man den Kapillareffekt, indem eine Lösung auf ein Spezialpapier getropft wird und an diesem aufsteigt, wobei Bestandteile der Lösung mitgetragen werden. Aufgrund der unterschiedlichen Laufweite können die Stoffe getrennt werden.
Medizin: Um kleine Mengen Blut abzuzapfen, kann man einen kleinen Einstich in die Gefäße an den Fingern oder am Ohrläppchen vornehmen und an das austretende Blut ein dünnes Sammelröhrchen halten, in dem das Blut aufgrund des Kapillareffektes aufsteigt und somit gesammelt werden kann.
Textilien: Eine ähnliche Saugwirkung wie beim Papier lässt sich auch bei Putzlappen bzw. Stoffen beobachten. Das Gleiche gilt auch für Schwämme. Für Papier, Putzlappen und Schwämme gilt dabei: Je größer die innere Oberfläche (pro Volumen), desto größer auch die Saugwirkung.

Löten: Auch beim Löten tritt der Effekt auf: Das flüssige Lot fließt durch die Kapillarwirkung beispielsweise in den Spalt von Kupferrohrfittings. Zum Entlöten von elektronischen Bauelementen von Leiterplatten wird häufig ein Drahtgeflecht, die Entlötlitze, verwendet.
An der Form des Lötkegels wird die Qualität des Lötergebnisses unmittelbar erkennbar. Sollte dieser nicht konkav und auf der Platine flach auslaufend sein, handelt es sich höchstwahrscheinlich um eine kalte Lötstelle. Durch die Kapillarität sind auch Lötungen „über Kopf“ möglich.

Bauwesen: Im Bauwesen spielt die Kapillarität eine herausragende Rolle. Ein Großteil der Maßnahmen zur Bauwerksabdichtung richtet sich gegen die in Bodenplatte und Wänden kapillar aufsteigende Feuchte. Bei oberirdischen Bauteilen haben kapillare Baustoffe demgegenüber den willkommenen Effekt, Feuchtigkeitsansammlungen großflächig zu verteilen. Wenn die Feuchtigkeit dabei eine Bauteiloberfläche erreicht, kann sie verdunsten. Durch den sogenannten Transpirationssog wird dann stetig Wasser nachgefördert, bis die Ausgleichsfeuchte erreicht ist. Kapillare Baustoffe können so auch größere Wassermengen aufnehmen und verteilen, die etwa als Folge eines Rohrbruchs Decken und Wände durchfeuchtet haben, bevor es zu Bauschäden und Schimmelbildung kommt.
Im Winter wird gewöhnlich an kalten Stellen der Außenwand der Taupunkt der Innenraumluft unterschritten, so dass Kondensat entsteht, das beim Lüften verdunstet und an die Außenluft abgegeben wird. Bildet sich zu viel Kondensat oder wird zu wenig gelüftet, dann sammelt sich die Feuchtigkeit in der Wand. Wände und Decken, die durchgehend aus kapillaraktiven Baustoffen bestehen, können die Feuchtigkeit absorbieren und an die Außenseite der Wand oder in Räume mit geringerem Feuchtigkeitsanfall leiten, wo sie verdunstet.
Sehr saugfähig sind traditionelle Ziegelsteine und Kalksandsteine, eine deutlich geringere Kapillarwirkung besteht bei hartgebrannten Ziegelsteinen (Klinker), Porenbeton und Beton. Um den Kapillarstrom in Gebäuden zu unterbrechen, werden im Fundamentbereich wasserdichte Trennschichten wie z. B. Bitumenbahnen eingebaut.
Önologie: In der Önologie werden zum Messen des Ethanolgehalts von Weinen Vinometer verwendet, in denen der Wein je nach Ethanolgehalt mehr oder weniger weit aufsteigt.
Formel (Kapillargleichung)

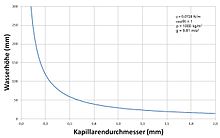
Die Steighöhe h einer Flüssigkeitssäule ist gegeben durch:
Dabei ist:
- = Oberflächenspannung
- θ = Kontaktwinkel
- ρ = Dichte der Flüssigkeit
- g = Schwerebeschleunigung
- r = Radius der Röhre
Für eine wassergefüllte Glasröhre, die gegen die Luft auf Meereshöhe (1.013,25 hPa) offen ist, ist:
- = 0,0728 J/m² bei 20 °C
- θ = 20° = 0,35 rad
- ρ = 1000 kg/m³
- g = 9,81 m/s²
so ergibt sich für die Steighöhe:
| Kapillarenradius | Steighöhe |
|---|---|
| 1000 mm | 0,014 mm |
| 100 mm | 0,14 mm |
| 10 mm | 1,4 mm |
| 1 mm | 14 mm |
| 0,1 mm | 140 mm |
| 0,01 mm | 1400 mm |
Die Washburn-Gleichung beschreibt kapillare Strömungen in porösen Materialien ohne Berücksichtigung der Gravitation.
Kapillaraufstieg zwischen zwei Glasplatten
Das Produkt der Schichtdicke (d) und der Höhe des Anstiegs (h) ist konstant (d·h = konstant). Die beiden Größen sind also umgekehrt proportional. Die Wasseroberfläche zwischen den Scheiben ist hyperbolisch.
- Wasser zwischen zwei Glasplatten
Kapillarsperre
Eine Kapillarsperre soll verhindern, dass Flüssigkeiten aufsteigen oder durch den Kapillareffekt bzw. Hebereffekt vom vorgesehenen Standort ablaufen. Beispiele:
- Am Rand von Folienteichen wird eine Teichfolie hochgeführt, um zu verhindern, dass der Kapillareffekt das Teichwasser im Sand oder Erdmaterial des Uferbereichs über den Rand der Abdichtung aufsteigen und dann durch den Hebereffekt abfließen lässt.[4] Die mindestens etwa 5 cm nach oben überstehende Folie wird mit Steinen, Kies oder Betonmörtel abgedeckt oder durch Pflanzenbewuchs (wasserseitig und außerhalb des Teichs) oder einen Ufersteg getarnt.
- Bei der Oberflächenabdichtung für Deponien und Altlasten werden Kapillarsperren zur Ableitung der Oberflächenabwässer eingesetzt.[5] Dabei wird eine grobkörnige Kiesschicht als Kapillarblock angelegt und darüber eine feinkörnige Kapillarschicht aus Sand oder Erdreich mit Gefälle aufgetragen. Von oben eindringendes Wasser wird im feinkörnigen Material durch Kapillarkräfte gehalten und rinnt entlang der Böschungsneigung zum Böschungsfuß ab, wo es durch Drainagerohre abgeleitet wird.[6]
- Eine Horizontalsperre hindert Wasser daran, in Mauerwerk kapillar aufzusteigen. Siehe: Aufsteigende Feuchte
- Eine kapillarbrechende Schicht vermeidet den Aufstieg der Bodenfeuchte unterhalb der Gründungssohle oder des Fußbodens eines Bauwerkes.
- Manche Dampfbremse werden wasserundurchlässig ausgeführt, um zugleich kapillares Saugen zu verhindern.
Weblinks
- Vorlesung Medizinische Physik: Oberflächenspannung und Kapillarität, Veterinärmedizinische Universität Wien ( vom 26. März 2012 im Internet Archive)
Literatur und Weblinks
- H. Schubert: Kapillarität in porösen Feststoffsystemen. Springer, Berlin 1982, ISBN 3-540-11835-7.
- Valentin L. Popov: Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation. Springer, 2009, ISBN 978-3-540-88836-9.
- Video: YOUNGscher Randwinkel und Kapillarität – wie hoch steigt Wasser in einer Kapillare?. Jakob Günter Lauth (SciFox) 2013, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/15673.
Einzelnachweise
- ↑ Pierre-Gilles de Gennes, Françoise Brochard-Wyart, David Quéré: Capillarity and Wetting Phenomena. Springer-Verlag, New York 2004, ISBN 978-1-4419-1833-8, 2.4 Capillary Rise in Tubes: Jurin's Law, doi:10.1007/978-0-387-21656-0 (springer.com [abgerufen am 25. Oktober 2023]).
- ↑ proholz.at ( vom 23. September 2011 im Internet Archive).
- ↑ George W. Koch, Stephen C. Sillett, Gregory M. Jennings, Stephen D. Davis: The limits to tree height. In: Nature. Band 428, 2004, S. 851–854, doi:10.1038/nature02417.
- ↑ Gartenteiche. S. 8 (eingeschränkte Vorschau in der Google-Buchsuche), zuletzt abgerufen im Februar 2020.
- ↑ Die Kapillarsperre. Innovative Oberflächenabdichtung für Deponien und Altlasten. Springer-Verlag 1999.
- ↑ Wolf-Ulrich Henken-Mellies, S. Melchior, B. Steinert: E 2-33 Kapillarsperren in Oberflächenabdichtungssystemen; LGA Landesgewerbeanstalt Bayern, Grundbauinstitut, Nürnberg, 2010, (PDF-Datei)









