Gleichseitiges Dreieck

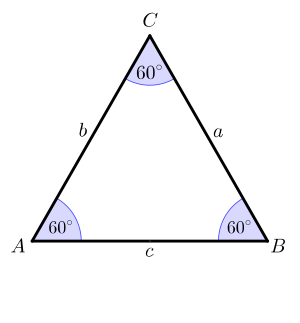
Ein gleichseitiges Dreieck ist ein Dreieck mit drei gleich langen Seiten bzw. Kanten sowie drei gleichen Winkeln von jeweils 60°. Ein gleichseitiges Dreieck wird auch als regelmäßiges Dreieck bezeichnet und zählt zu den regelmäßigen Polygonen. Alle gleichseitigen Dreiecke sind einander ähnlich. Gleichseitige Dreiecke sind rotationssymmetrisch (Drehung um den Mittelpunkt um 360°/3 = 120° oder Vielfache davon), spiegelsymmetrisch bezüglich der drei Mittelsenkrechten und spitzwinklig. Ihre Isometriegruppe ist die Diedergruppe D₃. Mit gleichseitigen Dreiecken ist die lückenlose Parkettierung einer Ebene möglich. Ein gleichseitiges Dreieck ist immer auch ein gleichschenkliges Dreieck, wobei hier nicht festgelegt ist, welche Seite die Basis ist. Die Menge der gleichseitigen Dreiecke ist also eine Teilmenge der Menge der gleichschenkligen Dreiecke.

Berechnung und Konstruktion

Ein gleichseitiges Dreieck ist durch eine Seitenlänge vollständig bestimmt (siehe Kongruenzsatz).

Mathematische Formeln zum gleichseitigen Dreieck
Flächeninhalt	$A={\frac {\sqrt {3}}{4}}\cdot a^{2}$
Umfang	$U=3\cdot a$
Seitenlängen	$a=b=c$
Winkel	$\alpha =\beta =\gamma =60^{\circ }$
Höhe	$h={\frac {\sqrt {3}}{2}}\cdot a$
Inkreisradius	$r_{i}={\frac {a}{2\cdot {\sqrt {3}}}}$
Umkreisradius	$r_{u}={\frac {a}{\sqrt {3}}}$

Die Konstruktion eines gleichseitigen Dreiecks mit Zirkel und Lineal ist einfach. Ist die Seitenlänge bzw. eine Seite als Strecke vorgegeben, so zeichnet man um die beiden Endpunkte der Strecke jeweils einen Kreis, dessen Radius die Strecke selbst ist. Jeder der beiden Schnittpunkte der Kreise bildet mit den Endpunkten der vorgegebenen Strecke ein gleichseitiges Dreieck.^[1]

Ist stattdessen der Umkreis des gleichseitigen Dreiecks vorgegeben, so zeichnet man zunächst eine Gerade durch den Kreismittelpunkt M. Diese schneidet den Kreis in zwei Punkten C und D. Dann schlägt man einen Kreisbogen mit dem Radius des Umkreises um den Punkt D. Dieser schneidet den Umkreis in den Punkten A und B. Die Punkte A, B und C sind die Ecken des gesuchten gleichseitigen Dreiecks.^[2]

Gleichseitiges Dreieck,
Seitenlänge vorgegeben

Gleichseitiges Dreieck,
Umkreis vorgegeben

Ausgezeichnete Punkte

Im gleichseitigen Dreieck schneiden sich die Höhen, die Mittelsenkrechten (Seitensymmetralen), die Seitenhalbierenden (Schwerelinien) und die Winkelhalbierenden in einem gemeinsamen Punkt. Daher sind auch die fünf ausgezeichneten Punkte, der Höhenschnittpunkt $H$ , der Umkreismittelpunkt $U$ , der Schwerpunkt $S$ , der Inkreismittelpunkt $I$ und der Mittelpunkt des Feuerbachkreises $F$ derselbe Punkt. Dieser Punkt teilt die Höhen, z. B. ${\tfrac {\overline {CI}}{\overline {DI}}}$ , im Verhältnis $2:1,$ d. h. $2r=R.$ Wie im nebenstehenden Bild erkennbar, fällt der Feuerbachkreis (hellblau) mit dem Inkreis (rot) zusammen; für beide gilt der gleiche Radius $r.$

Sätze

Konstruiert man über den Seiten eines beliebigen Dreiecks gleichseitige Dreiecke, so bilden die drei Schwerpunkte dieser gleichseitigen Dreiecke ein weiteres gleichseitiges Dreieck, das sogenannte Napoleon-Dreieck. Die Eigenschaft, dass die drei Schwerpunkte unabhängig von der Form des Ausgangsdreiecks immer ein gleichseitiges Dreieck bilden wird auch als Satz von Napoleon bezeichnet.

Das Morley-Dreieck ist ein weiteres gleichseitiges Dreieck, das aus einem beliebigen Dreieck durch bestimmte Konstruktionsvorschrift entsteht. Die Eigenschaft, dass man dabei immer ein gleichseitiges Dreieck erhält wird entsprechend als Satz von Morley bezeichnet.

Der Satz von Viviani besagt für einen Punkt im Inneren eines gleichseitigen Dreiecks, dass die Summe der Abstände des Punktes von den Dreiecksseiten der Länge der Höhe des Dreiecks entspricht.

Der Satz von Möbius-Pompeiu stellt für ein gleichseitiges Dreieck und einen beliebigen Punkt, der nicht auf dessen Umkreis liegt, fest, dass die Längen der drei Verbindungsstrecken des Punktes zu den Eckpunkten des Dreiecks stets die Dreiecksungleichung erfüllen, das heißt, dass ein Dreieck mit diesen Seitenlängen konstruiert werden kann. Liegt der Punkt auf dem Umkreis des gleichseitigen Dreiecks, so erhält man ein entartetes Dreieck und die Länge der längsten Verbindungsstrecke entspricht der Summe der Längen der beiden kürzeren Verbindungsstrecken. Letztere Aussage nennt man auch den Satz von van Schooten.

Platons gleichseitiges Dreieck

Nachdem Platon die fünf platonischen Körper den Elementen zuordnet (Tetraeder–Feuer, Oktaeder–Luft, Ikosaeder–Wasser, Dodekaeder–Kosmos und Hexaeder–Erde), beschreibt er im Timaios (53b-56c) diejenigen regulären Vielecke, welche die Oberflächen der platonischen Körper bilden.^[3] Er unterteilt die Vielecke in besondere gleichseitige Dreiecke (direkt vorhanden in Tetraeder, Oktaeder und Ikosaeder bzw. virtuell in den Fünfeckflächen des Dodekaeders) sowie in besondere gleichschenklig-rechtwinkligen Dreiecke (virtuell vorhanden in den Quadratflächen des Hexaeders).

Nach Platon sind die gleichschenklig-rechtwinkligen Dreiecke alle zueinander ähnlich, dies gilt nicht für rechtwinklige Dreiecke mit ungleichen Schenkeln. Er wählt unter den letzteren aus (dabei meint er das rechtwinklige Dreieck mit den Winkeln $30^{\circ };\;60^{\circ };\;90^{\circ }$ ):

Zwei Dreiecke wollen wir also ausgewählt haben: eines das gleichschenklige und das andere dasjenige, in welchem das Quadrat der größeren Kathete das Dreifache von dem der kleineren beträgt.^[3]

Nimmt man als Baustein ein rechtwinkliges Dreieck, beispielsweise mit den Katheten $1$ und ${\sqrt {3}}$ sowie der Hypotenuse $2$ , erfüllt es Platons obige Bedingung. Die Zusammensetzung sechs solcher Dreiecke liefert das gleichseitige Dreieck mit den Seitenlängen $2\cdot {\sqrt {3}}$ .

Die Konstruktion eines solchen gleichseitigen Dreiecks ist einfach. Sie besteht aus neun Kreise mit dem Radius gleich $1$ (auch mit einem sogenannten kollabierenden Zirkel machbar), drei geraden Linien mit der Länge $2\cdot {\sqrt {3}}$ sowie aus drei Mittelsenkrechten mit der Länge $3$ .

Im Koordinatensystem

Mittelpunkt

Der Mittelpunkt $M$ , das heißt der Schnittpunkt der Mittelsenkrechten, Seitenhalbierenden und Höhen, eines Dreiecks mit Ecken $A=(x_{A}|y_{A})$ , $B=(x_{B}|y_{B})$ und $C=(x_{C}|y_{C})$ besitzt die folgenden Koordinaten:

{\begin{aligned}x_{M}&={\frac {1}{3}}(x_{A}+x_{B}+x_{C})\\y_{M}&={\frac {1}{3}}(y_{A}+y_{B}+y_{C})\end{aligned}}

Beispiel

Gegeben:

A=(1|5)

,

B=(4|4)

und

C=(1{,}633\ldots |1{,}901\ldots )

Gesucht:

M=\left(x_{M}|y_{M}\right)

x_{M}={\frac {1+4+1{,}633\ldots }{3}}=2{,}211\ldots ,\qquad y_{M}={\frac {5+4+1{,}902\ldots }{3}}=3{,}633\ldots

.

Somit ergibt sich

\;M=\left(2{,}211\ldots |3{,}633\ldots \right)

.

Dritter Eckpunkt

Sind vom gleichseitigen Dreieck die Koordinaten von zwei Ecken bekannt, so können die Koordinaten der dritten Ecke durch 60°-Drehung von Ecke B um Ecke A berechnet werden. Es gibt zwei Lösungen:

Gegeben:

A=(x_{A}|y_{A})

und

B=(x_{B}|y_{B})

Gesucht:

C=(x_{C}|y_{C})

{\begin{aligned}x_{C}&={\frac {x_{B}+x_{A}\pm {\sqrt {3}}\cdot (y_{B}-y_{A})}{2}}\\y_{C}&={\frac {y_{B}+y_{A}\mp {\sqrt {3}}\cdot (x_{B}-x_{A})}{2}}\end{aligned}}

Beispiel

Gegeben:

A=(3|5)

und

B=(6|4)

Gesucht:

C_{1}=\left(x_{C_{1}}|y_{C_{1}}\right)

und

C_{2}=\left(x_{C_{2}}|y_{C_{2}}\right)

x_{C_{1}}={\frac {6+3+{\sqrt {3}}\cdot (4-5)}{2}}=3{,}634\ldots ,\qquad y_{C_{1}}={\frac {4+5-{\sqrt {3}}\cdot (6-3)}{2}}=1{,}902\ldots

.

x_{C_{2}}={\frac {6+3-{\sqrt {3}}\cdot (4-5)}{2}}=5{,}366\ldots ,\qquad y_{C_{2}}={\frac {4+5+{\sqrt {3}}\cdot (6-3)}{2}}=7{,}098\ldots

.

Somit ergibt sich

\;C_{1}=\left(3{,}634\ldots |1{,}902\ldots \right)

,

\;C_{2}=\left(5{,}366\ldots |7{,}098\ldots \right)

.

Parkettierungen mit gleichseitigen Dreiecken

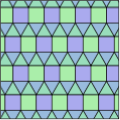
Einige platonische und archimedische Parkettierungen enthalten gleichseitigen Dreiecke. Diese Parkettierungen sind periodisch, drehsymmetrisch und translationssymmetrisch und enthalten ausschließlich regelmäßige Polygone.

Regelmäßiges Dreiecksgitter
3-3-3-4-4
3-3-4-3-4
3-6-3-6
3-3-3-3-6 (zwei gespiegelte Varianten)
3-4-6-4
3-12-12

Die Zahlen unter den Abbildungen geben an, wie viele Ecken die regelmäßigen Polygone haben, die jeweils an einem Punkt zusammenstoßen. Die Innenwinkel ergeben zusammen 360°.

Zerlegung in zwei kongruente regelmäßige Sechsecke

Ein gleichseitiges Dreieck, dessen Seite ohne Beschränkung der Allgemeinheit die Länge 1 hat, lässt sich so in zwölf kongruente gleichschenklige Dreiecke zerlegen, dass man hieraus zwei kongruente regelmäßige Sechsecke mit der Seitenlänge $s={\frac {\sqrt {3}}{6}}$ bilden kann.

Die Aussage $s={\frac {\sqrt {3}}{6}}$ folgt nach elementaren algebraischen Umformungen aus dem Ansatz

\cos 30^{\circ }={\frac {\frac {1}{4}}{s}}

gemäß der abgebildeten Beweisfigur.^[4]

Spiralen

Gegeben sei eine unendliche Folge gleichseitiger Dreiecke, in der jedem Dreieck $D_{n}$ jeweils das nachfolgende Dreieck $D_{n+1}$ so einbeschrieben ist, dass jede Seite von $D_{n}$ durch den Eckpunkt des Nachfolgers $D_{n+1}$ halbiert wird. O.B.d.A. wird der Seite des Ausgangsdreiecks $D_{1}$ die Länge 1 zugeordnet. Dann gilt:

Linienspirale

Ist

a_{n}

die halbe Seitenlänge des n-ten gleichseitigen Dreiecks (Figur 1), so ist

\left(a_{n}\right)_{n\in \mathbb {N} }

eine geometrische Folge mit dem Bildungsgesetz

a_{n}=\left({\tfrac {1}{2}}\right)^{n}

und dem Grenzwert^[5]

a={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots =

\sum _{n=1}^{\infty }\left({\frac {1}{2}}\right)^{n}={\frac {\frac {1}{2}}{1-{\frac {1}{2}}}}=1

.

Flächenspirale

Beträgt

A_{n}

ein Viertel der Flächenmaßzahl des n-ten gleichseitigen Dreiecks (Figur 2), so ist

\left(A_{n}\right)_{n\in \mathbb {N} }

eine geometrische Folge mit dem Bildungsgesetz

A_{n}=\left({\tfrac {1}{4}}\right)^{n}

und dem Grenzwert^[5]

A={\frac {1}{4}}+{\frac {1}{16}}+{\frac {1}{64}}+\cdots =

\sum _{n=1}^{\infty }\left({\frac {1}{4}}\right)^{n}={\frac {\frac {1}{4}}{1-{\frac {1}{4}}}}={\frac {1}{3}}

.

Die Folgen $\left(a_{n}\right)_{n\in \mathbb {N} }$ und $\left(A_{n}\right)_{n\in \mathbb {N} }$ lassen sich geometrisch jeweils als Spirale darstellen.^[5]

Polyeder mit gleichseitigen Dreiecken

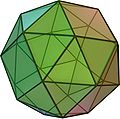
Einige besondere Polyeder haben gleichseitige Dreiecke als Seitenflächen, zum Beispiel das regelmäßige Tetraeder, das Oktaeder und das Ikosaeder. Dies sind die einzigen platonischen Körper, die Dreiecke enthalten. Auch einige archimedische Körper enthalten gleichseitige Dreiecke, vor allem das abgeschrägte Hexaeder und das abgeschrägte Dodekaeder. Polyeder, die ausschließlich kongruente gleichseitige Dreiecke als Seitenflächen haben, werden Deltaeder genannt.

Tetraeder
Oktaeder
Ikosaeder
Abgeschrägtes Hexaeder
Abgeschrägtes Dodekaeder
Dreifach erweitertes Dreiecksprisma (ein Deltaeder)
Zweifach erweitertes Antiprisma (ein Deltaeder)

Anwendungsbeispiel im Alltag

Das Foto zeigt zwei zu einer Raute positionierte Schachtdeckel in Form von zwei kongruenten gleichseitigen Dreiecken. In jedem der beiden Dreiecke sind die Höhen ersichtlich.

Siehe auch

Literatur

Jozsef Sandor: On the Geometry of Equilateral Triangles. In: Forum Geometricorum. Band 5, 2005, S. 107–117 (englisch, fau.edu [PDF; 75 kB]).

Weblinks

Commons: Gleichseitiges Dreieck – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Gleichseitiges Dreieck – Lern- und Lehrmaterialien

Eric W. Weisstein: gleichseitiges Dreieck. In: MathWorld (englisch).
Gleichseitiges Dreieck auf mathematische-basteleien.de

Einzelnachweise

↑ Johann Friedrich Lorenz: Euklid’s Geometrie oder die sechs ersten Bücher der Elemente nebst dem eilften und zwölften. Waisenhaus-Buchhandlung, Halle / Berlin 1818, Erstes Buch: Der 1. Satz. Aufgabe. …, S. 5 (babel.hathitrust.org).
↑ Johannes Kepler: Weltharmonik. übersetzt und eingeleitet von Max Caspar. 1939, XXXVIII. Satz: Seiten des Dreiecks …, S. 37. (Neuauflage: Verlag R. Oldenbourg, München 2006. eingeschränkte Vorschau in der Google-Buchsuche)
↑ ^a ^b Dietmar Herrmann: Die antike Mathematik. 7.1 Die schönsten Dreiecke Platons. Springer-Verlag, Berlin, Heidelberg 2014, ISBN 978-3-642-37611-5, S. 63–65.
↑ Eckard Specht, Erhard Quaisser, Patrick Bauermann (Hrsg.): 50 Jahre Bundeswettbewerb Mathematik - Die schönsten Aufgaben Zweite, erweiterte Auflage, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2020, ISBN 978-3-662-61165-4, S. 135–139
↑ ^a ^b ^c Hans Walser: Spiralen, Schraubenlinien und spiralartige Figuren - Mathematische Spielereien in zwei und drei Dimensionen, Springer Spektrum, Springer-Verlag GmbH Berlin 2022, ISBN 978-3-662-65131-5, Seiten 67–69

[1] Johann Friedrich Lorenz: Euklid’s Geometrie oder die sechs ersten Bücher der Elemente nebst dem eilften und zwölften. Waisenhaus-Buchhandlung, Halle / Berlin 1818, Erstes Buch: Der 1. Satz. Aufgabe. …, S. 5 (babel.hathitrust.org).

[2] Johannes Kepler: Weltharmonik. übersetzt und eingeleitet von Max Caspar. 1939, XXXVIII. Satz: Seiten des Dreiecks …, S. 37. (Neuauflage: Verlag R. Oldenbourg, München 2006. eingeschränkte Vorschau in der Google-Buchsuche)

[Herrmann-3] Dietmar Herrmann: Die antike Mathematik. 7.1 Die schönsten Dreiecke Platons. Springer-Verlag, Berlin, Heidelberg 2014, ISBN 978-3-642-37611-5, S. 63–65.

[4] Eckard Specht, Erhard Quaisser, Patrick Bauermann (Hrsg.): 50 Jahre Bundeswettbewerb Mathematik - Die schönsten Aufgaben Zweite, erweiterte Auflage, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2020, ISBN 978-3-662-61165-4, S. 135–139

[Walser-5] Hans Walser: Spiralen, Schraubenlinien und spiralartige Figuren - Mathematische Spielereien in zwei und drei Dimensionen, Springer Spektrum, Springer-Verlag GmbH Berlin 2022, ISBN 978-3-662-65131-5, Seiten 67–69

[1]

[2]

[3]

[4]

[5]

Fahrer / Team für die Suche eingeben:

Fahrer / Team für die Suche eingeben:

Langbahn Team – Weltmeisterschaft

Gleichseitiges Dreieck

Inhaltsverzeichnis

Berechnung und Konstruktion

Ausgezeichnete Punkte

Sätze

Platons gleichseitiges Dreieck

Im Koordinatensystem

Mittelpunkt

Dritter Eckpunkt

Parkettierungen mit gleichseitigen Dreiecken

Zerlegung in zwei kongruente regelmäßige Sechsecke

Spiralen

Polyeder mit gleichseitigen Dreiecken

Anwendungsbeispiel im Alltag

Siehe auch

Literatur

Weblinks

Einzelnachweise