Gauß-Quadratur
Die Gauß-Quadratur (nach Carl Friedrich Gauß) ist ein Verfahren zur numerischen Integration, das bei gegebenen Freiheitsgraden eine optimale Approximation des Integrals liefert. Bei diesem Verfahren wird die zu integrierende Funktion aufgeteilt in , wobei eine Gewichtsfunktion ist und durch ein spezielles Polynom mit speziell gewählten Auswertungspunkten approximiert wird. Dieses Polynom lässt sich exakt integrieren. Das Verfahren ist also von der Form
- .
Die Gewichtsfunktion ist größer gleich Null, hat endlich viele Nullstellen und ist integrierbar. ist eine stetige Funktion. Der Integrationsbereich ist nicht auf endliche Intervalle beschränkt. Weiterhin werden als Knoten, Abszissenwerte oder Stützstellen und die Größen als Gewichte bezeichnet.
Das Verfahren wurde 1814 von Gauß veröffentlicht,[1] und Carl Gustav Jacobi hat es 1826 in die heutige Form mit orthogonalen Polynomen gebracht.[2] Gauß-Quadraturen finden in allen Bereichen Anwendung, in denen numerische Integrale durchgeführt werden müssen, so im Besonderen beim Wissenschaftlichen Rechnen, in den Ingenieurwissenschaften und in der Numerik. Eine besonders häufige Anwendung der Gauß-Quadratur findet sich in der Finite-Elemente-Methode, dort wird diese benötigt, um über Elemente zu integrieren.
Eigenschaften
Um optimale Genauigkeit zu erreichen, müssen die Abszissenwerte einer Gauß-Quadraturformel vom Grad genau den Nullstellen des -ten orthogonalen Polynoms vom Grad entsprechen. Die Polynome , , …, müssen dabei orthogonal bezüglich des mit gewichteten Skalarprodukts sein,
Für die Gewichte gilt:
Die Gauß-Quadratur stimmt für polynomiale Funktionen , deren Grad maximal ist, mit dem Wert des Integrals exakt überein. Es lässt sich zeigen, dass keine Quadraturformel existiert, die alle Polynome vom Grad exakt integriert. In dieser Hinsicht ist die Ordnung des Quadraturverfahrens optimal.
Ist die Funktion hinreichend glatt, d. h. ist sie mal stetig differenzierbar in , so kann für den Fehler der Gaußquadratur mit Stützstellen und dem Leitkoeffizient des Polynoms gezeigt werden:[3]
- für ein .
Anwendung
Die gaußsche Quadratur findet Anwendung bei der numerischen Integration. Dabei werden für eine gegebene Gewichtsfunktion und einen gegebenen Grad n, der die Genauigkeit der numerischen Integration bestimmt, einmalig die Stützpunkte und Gewichtswerte berechnet und tabelliert. Anschließend kann für beliebige die numerische Integration durch einfaches Aufsummieren von gewichteten Funktionswerten erfolgen.
Dieses Verfahren ist damit potentiell vorteilhaft
- wenn viele Integrationen mit derselben Gewichtsfunktion durchgeführt werden müssen und
- wenn hinreichend gut durch ein Polynom approximierbar ist.
Für einige spezielle Gewichtsfunktionen sind die Werte für die Stützstellen und Gewichte fertig tabelliert.
Gauß-Legendre-Integration
Dies ist die bekannteste Form der Gauß-Integration auf dem Intervall , sie wird oft auch einfach als Gauß-Integration bezeichnet. Es gilt . Die resultierenden orthogonalen Polynome sind die Legendre-Polynome erster Art. Der Fall ergibt die Mittelpunktsregel. Wir erhalten mit den Stützpunkten und den zugehörige Gewichten die Approximation
- .
Die Erweiterung auf beliebige Intervalle erfolgt durch eine Variablentransformation:
- .
Die Stützpunkte (auch Gaußpunkte genannt) und Gewichte der Gauß-Legendre-Integration sind:
| n=1 | ||
| 1 | 0 | 2 |
| n=2 | ||
| 1 | 1 | |
| 2 | 1 | |
| n=3 | ||
| 1 | ||
| 2 | 0 | |
| 3 | ||
| n=4 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| n=5 | ||
| 1 | ||
| 2 | ||
| 3 | 0 | |
| 4 | ||
| 5 |
Gauß-Tschebyschow-Integration
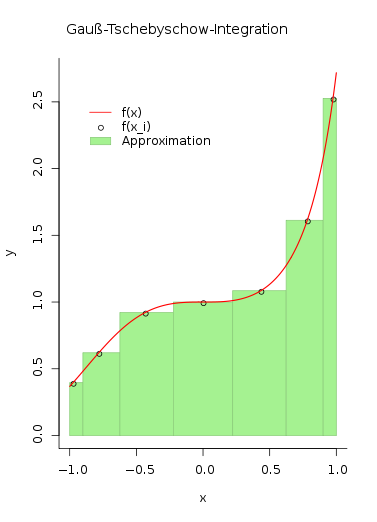
Eine Variante der Gauß-Integration auf dem Intervall ist jene mit der Gewichtsfunktion . Die dazugehörigen orthogonalen Polynome sind die Tschebyschow-Polynome, deren Nullstellen und damit auch die Stützpunkte der Quadraturformel direkt in analytischer Form vorliegen:
während die Gewichte nur von der Anzahl der Stützpunkte abhängen:
- .
Die Erweiterung auf beliebige Intervalle erfolgt durch eine Variablentransformation (siehe unten). Das gesuchte Integral kann umgeformt werden in . Zur numerischen Berechnung wird das Integral nun durch die Summe approximiert. Durch Einsetzen der Stützpunkte in analytischer Form erhält man
- ,
was der n-fachen Anwendung der Mittelpunktsregel über dem Intervall 0 bis Pi entspricht. Der Fehler kann für einen geeigneten Wert für t zwischen 0 und Pi abgeschätzt werden über
Gauß-Hermite-Integration
Gauß-Integration auf dem Intervall . Es gilt . Die resultierenden orthogonalen Polynome sind die Hermite-Polynome. Das gesuchte Integral kann umgeformt werden in . Zur numerischen Berechnung wird es nun durch die Summe approximiert.
Stützpunkte und Gewichte der Gauß-Hermite-Integration:
| n=1 | |||
| 1 | 0 | 1,7724538509055159 | |
| n=2 | |||
| 1 | 1,46114118266 | ||
| 2 | 1,46114118266 | ||
| n=3 | |||
| 1 | 1,32393117521 | ||
| 2 | 0 | 1,1816359006 | |
| 3 | 1,32393117521 | ||
| n=4 | |||
| 1 | −1,65068012389 | 0,0813128354472 | 1,2402258177 |
| 2 | −0,524647623275 | 0,804914090006 | 1,05996448289 |
| 3 | 0,524647623275 | 0,804914090006 | 1,05996448289 |
| 4 | 1,65068012389 | 0,0813128354472 | 1,2402258177 |
Gauß-Laguerre-Integration
Gauß-Integration auf dem Intervall . Es gilt . Die resultierenden orthogonalen Polynome sind die Laguerre-Polynome. Das gesuchte Integral kann umgeformt werden in . Zur numerischen Berechnung wird es nun durch die Summe approximiert.
Stützpunkte und Gewichte der Gauß-Laguerre-Integration:
| n=1 | |||
| 1 | 1 | 1 | 2,7182818284590451 |
| n=2 | |||
| 1 | 1,53332603312 | ||
| 2 | 4,45095733505 | ||
| n=3 | |||
| 1 | 0,415774556783 | 0,711093009929 | 1,07769285927 |
| 2 | 2,29428036028 | 0,278517733569 | 2,7621429619 |
| 3 | 6,28994508294 | 0,0103892565016 | 5,60109462543 |
| n=4 | |||
| 1 | 0,322547689619 | 0,603154104342 | 0,832739123838 |
| 2 | 1,74576110116 | 0,357418692438 | 2,04810243845 |
| 3 | 4,53662029692 | 0,038887908515 | 3,63114630582 |
| 4 | 9,3950709123 | 0,000539294705561 | 6,48714508441 |
Gauß-Lobatto-Integration
Mit dieser nach Rehuel Lobatto benannten Version wird auf dem Intervall integriert, wobei zwei der Stützstellen an den Enden des Intervalls liegen. Die Gewichtsfunktion ist . Polynome bis zum Grad werden exakt integriert.
Dabei ist , und bis sind die Nullstellen der ersten Ableitung des Legendre-Polynoms . Die Gewichte sind
Mit ergibt sich die Sehnentrapezregel und mit die Simpsonregel.
| n=2 | ||
| n=3 | ||
| n=4 | ||
| n=5 | ||
| n=6 | ||
| n=7 | ||
Variablentransformation bei der Gauß-Quadratur
Ein Integral über wird auf ein Integral über zurückgeführt, bevor man die Methode der Gauß-Quadratur anwendet. Dieser Übergang kann durch mit und sowie und Anwendung der Integration durch Substitution mit auf folgende Weise geschehen:
Seien nun die Stützstellen und die Gewichte der Gauß-Quadratur über dem Intervall , bzw. . Deren Zusammenhang ist also durch
gegeben.
Adaptives Gauß-Verfahren
Da der Fehler bei der Gauß-Quadratur, wie oben erwähnt, abhängig von der Anzahl der gewählten Stützstellen ist und sich mit einer größeren Anzahl Stützstellen gerade der Nenner erheblich vergrößern kann, legt dies nahe, bessere Näherungen mit größerem zu erhalten. Die Idee ist, zu einer vorhandenen Näherung eine bessere Näherung, beispielsweise , zu berechnen, um die Differenz zwischen beiden Näherungen zu betrachten. Sofern der geschätzte Fehler eine gewisse absolute Vorgabe überschreitet, ist das Intervall aufzuteilen, sodass auf und die -Quadratur erfolgen kann. Jedoch ist die Auswertung einer Gauß-Quadratur ziemlich kostspielig, da insbesondere für im Allgemeinen neue Stützstellen berechnet werden müssen, sodass sich für die Gauß-Quadratur mit Legendre-Polynomen die adaptive Gauß-Kronrod-Quadratur anbietet.
Adaptive Gauß-Kronrod-Quadratur
Die präsentierte Kronrod-Modifikation, welche nur für die Gauß-Legendre-Quadratur existiert, basiert auf der Verwendung der bereits gewählten Stützstellen und der Hinzunahme von neuen Stützstellen.[4] Während die Existenz optimaler Erweiterungen für die Gauß-Formeln von Szegö belegt wurde, leitete Kronrod (1965) für die Gauß-Legendre-Formeln optimale Punkte her, die den Präzisionsgrad sicherstellen.[4] Wenn die mithilfe der erweiterten Knotenzahl von berechnete Näherung als definiert wird, lautet die Fehlerschätzung:
Diese kann dann mit einem verglichen werden, um dem Algorithmus ein Abbruchkriterium zu geben. Die Kronrod-Knoten und -Gewichte zu den Gauß-Legendre-Knoten und -Gewichten sind für in der folgenden Tabelle festgehalten. Die Gauß-Knoten wurden mit einem (G) markiert.
| n=3 | ||
| 1 | ~0,960491268708020283423507092629080 | ~0,104656226026467265193823857192073 |
| 2 | ~0,774596669241483377035853079956480 (G) | ~0,268488089868333440728569280666710 |
| 3 | ~0,434243749346802558002071502844628 | ~0,401397414775962222905051818618432 |
| 4 | 0 (G) | ~0,450916538658474142345110087045571 |
| 5 | ~-0,434243749346802558002071502844628 | ~0,401397414775962222905051818618432 |
| 6 | ~-0,774596669241483377035853079956480 (G) | ~0,268488089868333440728569280666710 |
| 7 | ~-0,960491268708020283423507092629080 | ~0,104656226026467265193823857192073 |
| n=7 | ||
| 1 | ~0,991455371120812639206854697526329 | ~0,022935322010529224963732008058970 |
| 2 | ~0,949107912342758524526189684047851 (G) | ~0,063092092629978553290700663189204 |
| 3 | ~0,864864423359769072789712788640926 | ~0,104790010322250183839876322541518 |
| 4 | ~0,741531185599394439863864773280788 (G) | ~0,140653259715525918745189590510238 |
| 5 | ~0,586087235467691130294144838258730 | ~0,169004726639267902826583426598550 |
| 6 | ~0,405845151377397166906606412076961 (G) | ~0,190350578064785409913256402421014 |
| 7 | ~0,207784955007898467600689403773245 | ~0,204432940075298892414161999234649 |
| 8 | 0 (G) | ~0,209482141084727828012999174891714 |
| 9 | ~-0,207784955007898467600689403773245 | ~0,204432940075298892414161999234649 |
| 10 | ~-0,405845151377397166906606412076961 (G) | ~0,190350578064785409913256402421014 |
| 11 | ~-0,586087235467691130294144838258730 | ~0,169004726639267902826583426598550 |
| 12 | ~-0,741531185599394439863864773280788 (G) | ~0,140653259715525918745189590510238 |
| 13 | ~-0,864864423359769072789712788640926 | ~0,104790010322250183839876322541518 |
| 14 | ~-0,949107912342758524526189684047851 (G) | ~0,063092092629978553290700663189204 |
| 15 | ~-0,991455371120812639206854697526329 | ~0,022935322010529224963732008058970 |
Mehrdimensionale Gauß-Quadratur
Vor allem für die numerische Integration in der Finite-Elemente-Methode werden immer wieder numerische 2D und 3D-Integrale durchgeführt.[5][6] Für eine 2D Gauß-Quadratur gilt
mit als Jacobi-Matrix für die isoparametrische FEM-Transformation. Analog dazu kann auch die 3D Gauß-Quadratur durchgeführt werden, für die dann gilt
- .
Für die nachfolgenden Tabellen gilt dann bzw. .
Dreiecke
Die Berechnung der Gauß-Koordinaten und Gewichte ist für Dreiecke nicht trivial. Verschiedene Forscher im Bereich der Finiten Elemente haben unterschiedliche Gauß-Koordinaten und Gewichte errechnet und sind, vor allem für höhergradige Interpolation, zu unterschiedlichen Ergebnissen gekommen.[7] Eine relativ genaue numerische Integration ist aber mit allen errechneten Gauß-Koordinaten möglich. Die Normalkoordinaten sind im Fall der Dreiecke auf Einheitsdreiecke bezogen mit Schenkellänge 1 in Richtung der x- und y-Koordinate. In der folgenden Tabelle sind die Koordinaten mit den korrelierenden Gewichten angegeben. In der Klammer neben dem Grad ist das, falls es eines gibt, jeweils dazu passende Element angegeben.
| Grad | Normalkoordinaten[8] | Baryzentrische Koordinaten | |||||
| n=1 | |||||||
| 1 | 0,5 | 1 | |||||
| n=2 (TRI3) | |||||||
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| n=3 | |||||||
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
Vierecke
Für Vierecke ist die Berechnung der Koordinaten analog zu dem 1D-Fall zu führen. Während die Koordinaten dieselben bleiben, müssen die Gewichte an die erhöhte Punktanzahl angepasst werden, indem diese jeweils quadriert werden. Normalerweise wird in der Finite-Elemente-Methode die Gauß-Legendre-Integration durchgeführt. Es ergeben sich für die ersten 3 Grade die folgenden Koordinaten und Gewichte im Basisquadrat wie in der nachfolgenden Tabelle. In der Klammer neben dem Grad ist das, falls es eines gibt, jeweils dazu passende Element angegeben.
| n=1 | |||
| 1 | 0 | 0 | 4 |
| n=2 (QUAD4) | |||
| 1 | 1 | ||
| 2 | 1 | ||
| 3 | 1 | ||
| 4 | 1 | ||
| n=3 (QUAD8) | |||
| 1 | 0 | 0 | |
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | 0 | ||
| 7 | 0 | ||
| 8 | 0 | ||
| 9 | 0 |
Die Summe der Gewichte über alle Punkte muss sich für Quadrate immer jeweils 4 zu ergeben.
3D-Elemente
Für Elemente in drei Dimensionen verhalten sich die Berechnungen der Gauß Koordinaten gleich wie im 2D Fall. Für Tetraeder ist die Berechnung ebenfalls nicht trivial und auch nicht eindeutig. Für Hexaeder ergeben sich die Gauß Koordinaten analog zum 2D Fall. Die Koordinaten müssen nur auf die dritte Dimension erweitert werden, was für den dritten Grad dann zum Beispiel 27 Gauß-Punkte ergibt, und die Gewichte werden im Gegensatz zum 2D Fall nicht quadriert, sondern kubiert beziehungsweise analog zum 2D Fall je nach Position angepasst. Für Hexaeder ergeben sich die Gauß-Koordinaten bis Grad 2 wie in nachfolgender Tabelle. In der Klammer neben dem Grad ist das, falls es eines gibt, jeweils dazu passende Element angegeben.
| n=1 | ||||
| 1 | 0 | 0 | 0 | 8 |
| n=2 (HEXA8) | ||||
| 1 | 1 | |||
| 2 | 1 | |||
| 3 | 1 | |||
| 4 | 1 | |||
| 5 | 1 | |||
| 6 | 1 | |||
| 7 | 1 | |||
| 8 | 1 |
Weblinks
- efunda: Abscissas and Weights of Gauss-Laguerre Integration
- WolframMathWorld:Numerische Integration (englisch)
Literatur
- Philip J. Davis, Philip Rabinowitz: Methods of Numerical Integration. 2. Auflage. Academic Press, Orlando FL u. a. 1984, ISBN 0-12-206360-0.
- Vladimir Ivanovich Krylov: Approximate Calculation of Integrals. MacMillan, New York NY u. a. 1962.
- Arthur H. Stroud, Don Secrest: Gaussian Quadrature Formulas. Prentice-Hall, Englewood Cliffs NJ 1966.
- Arthur H. Stroud: Approximate Calculation of Multiple Integrals. Prentice-Hall, Englewood Cliffs NJ 1971, ISBN 0-13-043893-6.
- Martin Hermann: Numerische Mathematik, Band 2: Analytische Probleme. 4., überarbeitete und erweiterte Auflage. Walter de Gruyter Verlag, Berlin und Boston 2020, ISBN 978-3-11-065765-4.
- Daryl. L. Logan: A First Course in the Finite Element Method: SI Edition 6. Auflage, 1986, ISBN 978-1-305-63734-4
- Edward L. Wilson: Three-Dimensional Static and Dynamic Analysis of Structures 3. Edition, Computers and Structures, Inc., Berkeley 2002, ISBN 0-923907-00-9
- Bastian von Harrach: Einführung in die Numerik Skript: Goethe-Universität Frankfurt am Main – Institut für Mathematik, 2015
Quellen
- ↑ Methodus nova integralium valores per approximationem inveniendi. In: Comm. Soc. Sci. Göttingen Math. Band 3, 1815, S. 29–76, Gallica, datiert 1814, auch in Werke, Band 3, 1876, S. 163–196.
- ↑ C. G. J. Jacobi: Ueber Gauß’ neue Methode, die Werthe der Integrale näherungsweise zu finden. In: Journal für Reine und Angewandte Mathematik. Band 1, 1826, S. 301–308, (online), und Werke, Band 6.
- ↑ Philip J. Davis: Interpolation and approximation. [1st ed.]. Blaisdell Pub. Co, New York 1963, ISBN 978-0-486-62495-2, S. 344.
- ↑ a b Robert Piessens, Elise de Doncker-Kapenga, Christoph W. Überhuber, David K. Kahaner: QUADPACK: A subrotine package for automatic integration. Springer-Verlag, Berlin / Heidelberg / New York 1983, S. 16–17.
- ↑ Why do FEA engineers use 1D, 2D, 3D elements ? In: FEA for All. 12. März 2015, abgerufen am 30. September 2024 (amerikanisches Englisch).
- ↑ Łukasz Skotny Ph.D: What are the Types of Elements Used in FEA? In: Enterfea. 28. Februar 2019, abgerufen am 30. September 2024 (englisch).
- ↑ Cubature rules on the triangle (simplex). In: Universität Padua. Universität Padua, abgerufen am 22. September 2024 (englisch).
- ↑ D.A. Dunavant: High Degree Efficient Symmetrical Gaussian Quadrature Rules for the Triangle. In: International Journal for Numerical Methods in Engineering. Nr. 21(6).







![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)














![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)











































































































![{\displaystyle \left[a,{\frac {a+b}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2340575cf6aac755487555f6b71544a147ad4381)
![{\displaystyle \left[{\frac {a+b}{2}},b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5cd05ef535fe28124252885904819a07c058d8e)

































