Datei:NonConvex.gif
NonConvex.gif (360 × 392 Pixel, Dateigröße: 782 KB, MIME-Typ: image/gif, Endlosschleife, 84 Bilder, 4,2 s)
![]()
Diese Datei und die Informationen unter dem roten Trennstrich werden aus dem zentralen Medienarchiv Wikimedia Commons eingebunden.
Beschreibung
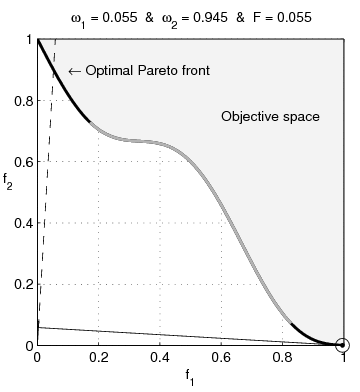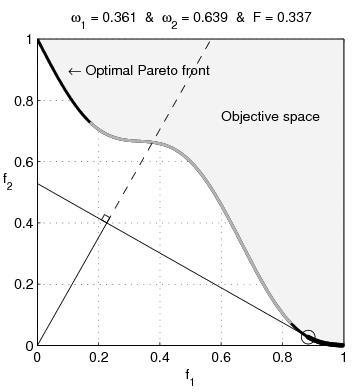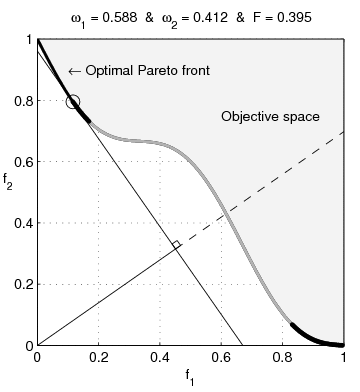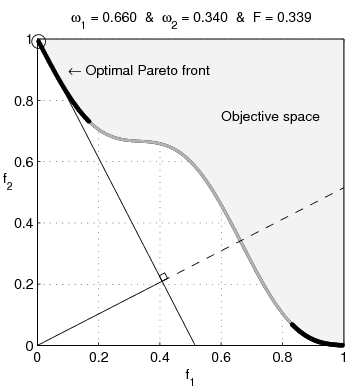
| BeschreibungNonConvex.gif | English: Weighted-sum approach is an easy method used to solve multi-objective optimization problem. It consists in aggregating the different optimization functions in a single function. However, this method only allows to find the supported solutions of the problem (i.e. points on the convex hull of the objective set). This animation shows that when the outcome set is not convex, not all efficient solutions can be found Français : La méthode des sommes pondérées est une méthode simple pour résoudre des problèmes d'optimisation multi-objectif. Elle consiste à aggréger l'ensemble des fonctions dans une seule fonction avec différents poids. Toutefois, cette méthode permet uniquement de trouver les solutions supportées (càd les points non-dominés appartenant à l'enveloppe convexe de l'espace d'arrivée). Cette animation montre qu'il n'est pas possible d'identifier toutes les solutions efficaces lorsque l'espace d'arrivée est n'est pas convexe. |
| Datum | |
| Quelle | Eigenes Werk |
| Urheber | Guillaume Jacquenot |
Source code (MATLAB)
function MO_Animate(varargin)
% This function generates objective space images showing why
% sum-weighted optimizer can not find all non-dominated
% solutions for non convex objective spaces in multi-ojective
% optimization
%
% Guillaume JACQUENOT
if nargin == 0
% Simu = 'Convex';
Simu = 'NonConvex';
save_pictures = true;
interpreter = 'none';
end
switch Simu
case 'NonConvex'
a = 0.1;
b = 3;
stepX = 1/200;
stepY = 1/200;
case 'Convex'
a = 0.2;
b = 1;
stepX = 1/200;
stepY = 1/200;
end
[X,Y] = meshgrid( 0:stepX:1,-2:stepY:2);
F1 = X;
F2 = 1+Y.^2-X-a*sin(b*pi*X);
figure;
grid on;
hold on;
box on;
axis square;
set(gca,'xtick',0:0.2:1);
set(gca,'ytick',0:0.2:1);
Ttr = get(gca,'XTickLabel');
Ttr(1,:)='0.0';
Ttr(end,:)='1.0';
set(gca,'XTickLabel',[repmat(' ',size(Ttr,1),1) Ttr]);
Ttr = get(gca,'YTickLabel');
Ttr(1,:)='0.0';
Ttr(end,:)='1.0';
set(gca,'YTickLabel',[repmat(' ',size(Ttr,1),1) Ttr]);
if strcmp(interpreter,'none')
xlabel('f1','Interpreter','none');
ylabel('f2','Interpreter','none','rotation',0);
else
xlabel('f_1','Interpreter','Tex');
ylabel('f_2','Interpreter','Tex','rotation',0);
end
set(gcf,'Units','centimeters')
set(gcf,'OuterPosition',[3 3 3+6 3+6])
set(gcf,'PaperPositionMode','auto')
[minF2,minF2_index] = min(F2);
minF2_index = minF2_index + (0:numel(minF2_index)-1)*size(X,1);
O1 = F1(minF2_index)';
O2 = minF2';
[pF,Pareto]=prtp([O1,O2]);
fill([O1( Pareto);1],[O2( Pareto);1],repmat(0.95,1,3));
text(0.45,0.75,'Objective space');
text(0.1,0.9,'\leftarrow Optimal Pareto front','Interpreter','TeX');
plot(O1( Pareto),O2( Pareto),'k-','LineWidth',2);
plot(O1(~Pareto),O2(~Pareto),'.','color',[1 1 1]*0.8);
V1 = O1( Pareto); V1 = V1(end:-1:1);
V2 = O2( Pareto); V2 = V2(end:-1:1);
O1P = O1( Pareto);
O2P = O2( Pareto);
O1PC = [O1P;max(O1P)];
O2PC = [O2P;max(O2P)];
ConvH = convhull(O1PC,O2PC);
ConvH(ConvH==numel(O2PC))=[];
c = setdiff(1:numel(O1P), ConvH);
% Non convex
O1PNC = O1PC(c);
[temp, I1] = min(O1PNC);
[temp, I2] = max(O1PNC);
if ~isempty(I1) && ~isempty(I2)
plot(O1PC(c),O2PC(c),'-','color',[1 1 1]*0.7,'LineWidth',2);
end
p1 = (V2(1)-V2(2))/(V1(1)-V1(2));
hp = plot([0 1],[p1*(-V1(1))+V2(1) p1*(1-V1(1))+V2(1)]);
delete(hp);
Histo_X = [];
Histo_Y = [];
coeff = 0.02;
Sq1 = coeff *[0 1 1 0 0;0 0 1 1 0];
compt = 1;
for i = 2:1:length(V1)-1
if ismember(i,ConvH)
p1 = (V2(i+1)-V2(i-1))/(V1(i+1)-V1(i-1));
x_inter = 1/(1+p1^2)*(p1^2*V1(i)-p1*V2(i));
hp1 = plot([0 1],[p1*(-V1(i))+V2(i) p1*(1-V1(i))+V2(i)],'k');
% hp2 = plot([x_inter],[-x_inter/p1],'k','Marker','.','MarkerSize',8)
hp3 = plot([0 x_inter],[0 -x_inter/p1],'k-');
hp4 = plot([x_inter 1],[-x_inter/p1 -1/p1],'k--');
hp5 = plot(V1(i),V2(i),'ko','MarkerSize',10);
% Plot the square for perpendicular lines
alpha = atan(-1/p1);
Mrot = [cos(alpha) -sin(alpha);sin(alpha) cos(alpha)];
Sq_plot = repmat([x_inter;-x_inter/p1],1,5) + Mrot * Sq1;
hp7 = plot(Sq_plot(1,:),Sq_plot(2,:),'k-');
Histo_X = [Histo_X V1(i)];
Histo_Y = [Histo_Y V2(i)];
hp6 = plot(Histo_X,Histo_Y,'k.','MarkerSize',10);
w1 = p1/(p1-1);
w2 = 1-w1;
Fweight_sum = V1(i)*w1+w2*V2(i);
Fweight_sum = floor(1e3*Fweight_sum )/1e3;
w1 = floor(1000*w1)/1e3;
str1 = sprintf('%.3f',w1);
str2 = sprintf('%.3f',1-w1);
str3 = sprintf('%.3f',Fweight_sum);
if (strcmp(str1,'0.500')||strcmp(str1,'0,500')) && strcmp(Simu,'NonConvex')
disp('Two solutions');
end
title(['\omega_1 = ' str1 ' & \omega_2 = ' str2 ' & F = ' str3],'Interpreter','TeX');
axis([0 1 0 1]);
file = ['Frame' num2str(1000+compt)];
if save_pictures
saveas(gcf, file, 'epsc');
end
compt = compt +1;
pause(0.001);
delete(hp1);
delete(hp3);
delete(hp4);
delete(hp5);
delete(hp6);
delete(hp7);
end
end
disp(['Number of frames :' num2str(length(V1))]);
return;
function [A varargout]=prtp(B)
% Let Fi(X), i=1...n, are objective functions
% for minimization.
% A point X* is said to be Pareto optimal one
% if there is no X such that Fi(X)<=Fi(X*) for
% all i=1...n, with at least one strict inequality.
% A=prtp(B),
% B - m x n input matrix: B=
% [F1(X1) F2(X1) ... Fn(X1);
% F1(X2) F2(X2) ... Fn(X2);
% .......................
% F1(Xm) F2(Xm) ... Fn(Xm)]
% A - an output matrix with rows which are Pareto
% points (rows) of input matrix B.
% [A,b]=prtp(B). b is a vector which contains serial
% numbers of matrix B Pareto points (rows).
% Example.
% B=[0 1 2; 1 2 3; 3 2 1; 4 0 2; 2 2 1;...
% 1 1 2; 2 1 1; 0 2 2];
% [A b]=prtp(B)
% A =
% 0 1 2
% 4 0 2
% 2 2 1
% b =
% 1 4 7
A=[]; varargout{1}=[];
sz1=size(B,1);
jj=0; kk(sz1)=0;
c(sz1,size(B,2))=0;
bb=c;
for k=1:sz1
j=0;
ak=B(k,:);
for i=1:sz1
if i~=k
j=j+1;
bb(j,:)=ak-B(i,:);
end
end
if any(bb(1:j,:)'<0)
jj=jj+1;
c(jj,:)=ak;
kk(jj)=k;
end
end
if jj
A=c(1:jj,:);
varargout{1}=kk(1:jj);
else
warning([mfilename ':w0'],...
'There are no Pareto points. The result is an empty matrix.')
end
return;
The weighted-sum approach minimizes function 

where


such that


To have a non-convex outcome set, parameters 



Weights 


![{\displaystyle \omega _{1}\in [0;1]~}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99c8913e84daf282e85b04849cc18cc14594dda7)

Lizenz

|
Es ist erlaubt, die Datei unter den Bedingungen der GNU-Lizenz für freie Dokumentation, Version 1.2 oder einer späteren Version, veröffentlicht von der Free Software Foundation, zu kopieren, zu verbreiten und/oder zu modifizieren; es gibt keine unveränderlichen Abschnitte, keinen vorderen und keinen hinteren Umschlagtext.
Der vollständige Text der Lizenz ist im Kapitel GNU-Lizenz für freie Dokumentation verfügbar.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
- Dieses Werk darf von dir
- verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
- neu zusammengestellt werden – abgewandelt und bearbeitet werden
- Zu den folgenden Bedingungen:
- Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.
- Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten.
Kurzbeschreibungen
In dieser Datei abgebildete Objekte
Motiv
Urheber
Einige Werte ohne einen Wikidata-Eintrag
Urheberrechtsstatus
urheberrechtlich geschützt
Lizenz
GNU-Lizenz für freie Dokumentation Version 1.2 oder später
Creative Commons Namensnennung - Weitergabe unter gleichen Bedingungen 1.0
Creative Commons Namensnennung - Weitergabe unter gleichen Bedingungen 2.0
Creative Commons Namensnennung – Weitergabe unter gleichen Bedingungen 2.5 generisch
Creative Commons Namensnennung – Weitergabe unter gleichen Bedingungen 3.0 Generisch
Datum der Gründung, Erstellung, Entstehung, Erbauung
8. März 2009
Quelle der Datei
durch Hochlader erstelltes Original
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 18:13, 8. Mär. 2009 | 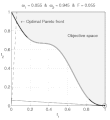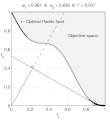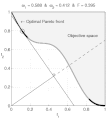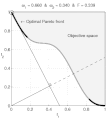 | 360 × 392 (782 KB) | Gjacquenot | {{Information |Description={{en|1=Weighted-sum approach is an easy method used to solve multi-objective optimization problem. It consists in aggregating the different optimization functions in a single function. However, this method only allows to find th |
Dateiverwendung
Die folgenden 2 Seiten verwenden diese Datei:
Globale Dateiverwendung
Die nachfolgenden anderen Wikis verwenden diese Datei:
- Verwendung auf ar.wikipedia.org
- Verwendung auf az.wikipedia.org
- Verwendung auf el.wikipedia.org
- Verwendung auf en.wikipedia.org
- Verwendung auf pt.wikipedia.org
- Verwendung auf ru.wikipedia.org
- Verwendung auf sr.wikipedia.org
- Verwendung auf zh.wikipedia.org