Benutzer:Hp.Baumeler/Verschiedene Entwürfe
UserBoxes
|
Die Variablen werden automatisch mit {{{nr}}} durchnummeriert oder mit zB "Jahrgang=" betitelt
Berechnung des Azimuts
Berechnung des Azimuts

Sind die geographischen Koordinaten des Standortes und die Koordinaten des Zielortes bekannt, wird das Azimut mit der sphärischen Trigonometrie am einfachsten in zwei Schritten berechnet. Im ersten Schritt wird die Distanz zwischen dem Standort und dem Zielort berechnet und im zweiten Schritt berechnet man das Azimut .
Das abgebildete sphärische Dreieck wird durch die drei Seiten und die drei Eckpunkte Standort, Nordpol und Zielort gebildet. Das Dreieck wird unter anderem mit dem sphärischen Seiten-Kosinussatz beschrieben:
Hier sind
wobei und die geographischen Breiten und und die geographischen Längen der beiden Orte sind. Obige Formel wird damit zu:
Die Distanz ist ein Segment eines Großkreises und wird in Winkelgraden ausgedrückt, wobei jede Bogenminute auf der Erdoberfläche einer Distanz von einer Seemeile entspricht.
Mit der berechneten Distanz sind die Werte aller drei Seiten bekannt und das Azimut kann im zweiten Schritt mit einem zweiten sphärischen Seiten-Kosinussatz berechnet werden:
Wieder ersetzt man und und es folgt:
Die Kosinusfunktion führt in der Umkehrfunktion (Arkuskosinus) immer zu zwei Winkelwerten. In unserem Falle zu und zu .
- Liegt der Zielort östlich des Standortes, so wird das berechnete Azimut
- Liegt der Zielort westlich des Standortes, so wird das berechnete Azimut (das normalerweise mit Werten von 0° bis 360° angegeben wird)
Bewegt man sich vom anfänglichen Standort auf einem Grosskreis, also entlang der Seite Richtung Ziel, so ändert sich das Azimut permanent. Das Azimut in Abhängigkeit der zurückgelegten Distanz kann mit dem (ersten) sphärischen Kotangenssatz hergeleitet werden. Zuerst berechnet man den Winkel . Das neue Azimut ist dann .
Hier ist wieder . ist hier das Azimut beim Start der Reise, das wir als schreiben und ist die zurückgelegte Distanz (in Winkelgraden), die wir hier, um nicht mit der Gesamtdistanz zu verwechseln, als schreiben. Zudem ersetzen wir . Die Distanz wird in den Winkel umgerechnet. Jede Seemeile (1.852 km) entspricht einer Bogenminute und jedes Grad hat 60 Bogenminuten.
Es folgt:
Beispiel

Sie befinden sich in El Golea (Algerien) und möchten durch die Sahara nach Farafra (Ägypten) marschieren. Die Koordinaten von El Golea und Farafra sind:
- El Golea: 30°36′53″N 002°52′22″E
- Farafra: 27°03′30″N 027°58′12″E
Diese Werte in die Distanzformel eingesetzt ergibt für die Distanz von El Golea bis Farafra , was auf der Erdoberfläche einer Distanz von 1333 NM oder 2470 km entspricht. Setzt man in einem zweiten Schritt die berechnete Distanz zusammen mit den Breiten der beiden Orte in der Azimutformel ein, so erhält man ein Azimut von .
Das hier berechnete Azimut beschreibt die Richtung, die man in El Golea nehmen muss, um auf kürzestem Wege nach Farafra zu gelangen. Marschiert man auf dem gegebenen Grosskreis, auf der kürzesten Verbindung also, so ändert sich das Azimut ständig.
Berechnet man das Azimut für eine Reise von Farafra nach El Golea, so erhält man mit der Azimutformel einen Winkel . Da der Zielort westlich des Standortes liegt, wird das Azimut .
Strahlenbrechung in der astronomischen Navigation
In der astronomischen Navigation wird mit einem Sextant die Höhe eines Gestirns über dem Horizont gemessen. Auf Grund der Strahlenbrechung ist die wahre Höhe des Gestirns immer geringer als die mit dem Sextant gemessene Höhe, wobei der Effekt für kleine Höhen markanter ist. Die gemessene Höhe muss korrigiert werden. Unten stehende Tabelle[1] zeigt für 10°C und den Normdruck (1013.2 hPa) die Zahl der Bogenminuten, die von der mit dem Sextant gemessenen Höhe abgezogen werden muss. Vor allem bei geringen Höhen ist die Korrektur massgebend, weil jede Bogenminute der Höhenmessung in der Ortsbestimmung zu einer Verschiebung der Position von einer Seemeile führt. Die hier beschriebene Korrektur der Strahlenbrechung ist eine der vier Beschikungen, die bei der Messung der Höhe des Gestirns durchgeführt werden müssen.
| Scheinbare Höhe | 0° | 1° | 2° | 3° | 14° | 5° | 6° | 7° | 8° | 9° | 10° |
| Brechung | 35.4' | 24.6' | 18.3' | 14.4' | 11.8' | 9.9' | 8.5' | 7.4' | 6.6' | 5.9' | 5.3' |
| Scheinbare Höhe | 12° | 14° | 16° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° |
| Brechung | 4.4' | 3.8' | 3.3' | 2.6' | 1.7' | 1.2' | 0.8' | 0.6' | 0.3' | 0.2' | 0.0' |
Bahnübergang
...
Technik

Bahnübergänge werden mit Tafeln, Andreaskreuzen und Lichtsignalen markiert und teilweise mit Bahnschranken gesichert. Bahnschranken werden meistens von einem Elektromotor angetrieben gesenkt und angehoben. Dieser Elektromotor befindet sich in der Regel ca. ein Meter über Boden direkt am Drehpunkt der Schranke. Früher, und an einigen Orten bis heute (2019), werden Bahnschranken mit einer Kurbel über Drahtzüge von Hand geschlossen und geöffnet. Ein Beispiel einer heute noch über Drahtzüge bedienten Schranke ist der Bahnübergang am Bahnhof Fridingen. Zur Sicherstellung, dass die Schranke bei Zugsdurchfahrt geschlossen ist, muss der Bahnbeamte von der Schrankenwinde einen Schlüssel, der nur bei geschlossener Barriere entfernt werden kann, am mechanischen Stellwerk einsetzen. Nur so wird es möglich, das Signal auf "Fahrt" zu setzen. Der Schlüssel kann, wenn ein Siganl auf "Fahrt" steht, nicht entfernt werden. Die Bahnschranke kann erst geöffnet werden, wenn der Schlüssel in der Schrankenwinde steckt und damit sichergestellt ist, dass alle Signale auf "Halt" gestellt sind. Passanten werden mit einem Glockenschlagwerk auf das Senken der Bahnschranke aufmerksam gemacht.
Bahnschranken auf offener Strecke wurden früher von einem Schrankenwärter bedient. Der Schrankenwärter wohnte oft gleich neben dem Bahnübergang in einem Bahnwärterhaus.
Sprache
afrikaans pad ‚deutsch: Strasse‘
englisch [], deutsch ‚Geringschätzung‘
Natürlich gekühlte Kühlräume

In warmen oder heissen, trockenen Gegenden ohne Strom oder Gas werden Kühlräume natürlich gekühlt. In Namibia zum Beispiel werden diese Räume Kühlraum oder auch nur Kühler genannt.
„Die Luft ist bei uns sehr trocken, Wasser verdunstet schnell. Das merkst Du an der Wäsche, die in kurzer Zeit trocknet. Und wo etwas verdunstet, entsteht Kühle.“
Kühler sind mit Doppelwänden gebaut, wobei die Aussenwand auf Lücke gemauert ist. Der Zwischenraum der Wände wird mit Holzkohle oder porösem Stein gefüllt, worüber Wasser gerieselt wird. Durch die Lücken der Aussenwand strömt trockene Luft und bringt das Wasser in der feuchten Kohle oder im porösen Stein zum verdunsten. Dadurch wird die Innenwand kalt und kühlt den ganzen Raum. Solche Kühlräume können selbst bei einer Aussentemperatur von 40 Grad auf einer Temperatur von 13 bis 17 Grad Celsius gehalten werden. Im Dach des Kühlraums ist meist ein vom Wind angetriebener Ventilator eingebaut.[2]
Einzelnachweise
- ↑ Auszug aus Fulst Nautische Tafeln, 24. Auflage, Arthur Geist Verlag, Bremen 1972
- ↑ a b Heimat Südwest, Schroedel Verlag KG, Hannover, Co-Autor: Walter Kahn Seite 81
Aus (Namibia)

xxxxxx Während der deutschen Kolonialzeit unterhielt die Schutztruppe hier einen Stützpunkt. Zu Beginn des Ersten Weltkriegs in Südwestafrika bauten die Deutschen in Aus eine Ersatzfunkstelle, da die Küstenfunkstelle in Lüderitzbucht am 14. September 1914 geräumt werden musste. xxxxxxxx
Aus war mit seiner Lage und seiner starken Befestigung gut geeignet um recht lange einer Belagerung standzuhalten.Der Funkbetrieb wurde in Aus bereits am 15.September aufgenommen. In Der Erste Weltkrieg im Schutzgebiet steht:
„In Aus entstanden zwei Antennentürme mit einer Höhe von 50 m. Zwischen den Türmen wurde eine dreidrahtige T-Antenne aufgehängt. Die Station hatte fast eine ähnliche Leistung, wie die in Lüderitzbucht. Die Verständigung mit der englischen Funkstation Slangkop und mit der neu eingerichteten englischen Funkstation in Lüderitzbucht war einwandfrei. Die französische Station Tabou (Elfenbeinküste) war weniger deutlich hörbar als von der früheren Lüderitzbuchter Station. Gut verständlich hingegen waren die Schiffsfunkstationen an der angolanischen sowie an der südwestafrikanischen Küste und an der Ostküste im Indischen Ozean bis etwa zur Höhe von Durban. Die Aufgabe der Station in Aus war es, Pressenachrichten abzuhören und unchiffrierte englische Befehle umgehend an den Gouverneur zu funken. Außerdem ermöglichte sie einen schnellen Kontakt zur Unionsregierung nach Pretoria und zu den britisch-südafrikanischen Kommandostellen. So konnten Informationen über Gefangene ausgetauscht werden. Außerdem konnte die Station in Aus auch den Funkverkehr stören. Sie trug dazu bei, den Kontakt auf Strecken, auf denen die Telegraphenleitung durchbrochen war, per Funk über die Stationen Windhoek und Tsumeb wieder herzustellen. Die Station arbeitete relativ lange und wurde erst am 27.März 1915 durch die Schutztruppe abgebaut, nachdem sie den Ort geräumt hatte. Was nicht abtransportierbar war, wurde gesprengt. Ansonsten wurde der Rest nach Tsumeb gebracht.“
Diskussion geogr Koord
Org:
Die geographischen Koordinaten (geographische Breite und geographische Länge) sind Kugelkoordinaten, mit denen sich die Lage eines Punktes auf der Erdoberfläche beschreiben lässt. Die Erde wird dabei in 180 Breitengrade und 360 Längengrade aufgeteilt. Breitenkreise verlaufen parallel zum Äquator, Längenkreise durch Nord- und Südpol.
Alternative:
Die geographischen Koordinaten sind Kugelkoordinaten, mit denen sich die Lage eines Punktes auf der Erdoberfläche beschreiben lässt. Die Breitengrade verlaufen vom Äquator (0°) ausgehend bis 90° Nord und 90° Süd an den Polen. Die Längengarde verlaufen vom Nullgradmeridian ausgehende 180° gegen Osten und 180° gegen Westen.
Kurvenflug
Physik
Kurvenradius

Um ein Flugzeug eine Kurve mit dem Radius fliegen zu lassen, muss das Flugzeug in Richtung Kurvenzentrum mit der Beschleunigung zentripedal beschleunigt werden. Um diese Beschleunigung zu erreichen, muss auf das Flugzeug der Masse eine zentripedale Kraft wirken. Diese Kraft wird mit dem Auftrieb der Flügel geschaffen, indem das Flugzeug in Richtung Kurvenzentrum gekippt wird. Der Auftrieb der Flügel wird beim Neigen des Flugzeuges vektoriell in eine senkrechte und in eine zentripedale (horizontale) Komponente geteilt. Die senkrechte, nach oben wirkende Komponente ist dem Gewicht des Flugzeuges entgegengerichtet und hat denselben Betrag wie das Gewicht: . Mit dem Flugzeug-Neigungswinkel (englisch bank-angle genannt) wird die zentripedale Kraft betragsmässig
und somit ist
Hier stellt die Erdbeschleunigung dar. Der Kurvenradius, den ein Flugzeug mit der Geschwindigkeit und einem Neigungswinkel fliegt ist:
Der Kurvenradius nimmt bei einem bestimmten Neigungswinkel im Quadrat mit der Geschwindigkeit zu und er ist unabhängig von der Grösse des betrachteten Flugzeuges (oder Vogels).
Beispiele
Eine Beechcraft Bonanza A36 fliegt im Reiseflug mit einer Geschwindigkeit von 160 kt (296 km/h). Bei einer Neigung von ist der Radius der geflogenen Kurve 1194 Meter.
Eine Linienflugzeug fliegt im Reiseflug mit einer Geschwindigkeit von zum Beispiel 450 kt (833 km/h). Bei einer Neigung von ist der Radius der geflogenen Kurve 9453 Meter.
Standardkurve
Man spricht von einer Standardkurve, wenn ein Flugzeug einen Kreis von 360° in zwei Minuten fliegt. Die im Kreis geflogene Distanz ist . Um diesen Kreis in zwei Minuten abzufliegen, muss das Flugzeug eine Querneigung von
haben. Für kleine Geschwindigkeiten ist
eine gute Näherung.
Eine Beechcraft Bonanza A36, die im Reiseflug eine Geschwindigkeit von 160 kt (296 km/h) hat, fliegt eine Standardkurve bei einer Querneigung von .
g-Faktor

Der in einer Kurve auf das Flugzeug und die Insassen wirkende g-Faktor, auch Lastvielfach genannt, ist das Verhältnis des in der Kurve benötigen Auftriebes () zum Auftrieb im Horizontalflug.
Der g-Faktor ist für Querneigungen bis zu 30° sehr gering und als Passagier kaum spürbar. Für Querneigungen über 30° steigt der g-Faktor steil an. Für jedes fliegende Objekt, sei es ein Flugzeug oder ein Vogel, ist das Lastvielfach unabhängig von Masse und unabhängig von der Geschwindigkeit bei einer Querneigung von 60° immer 2.
Wirkung der Kräfte auf Piloten und Passagiere
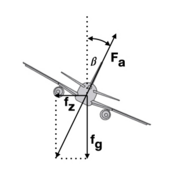
In der Kurve ist ein Flugzeug ein beschleunigtes System. Innerhalb dieses Systems wirken auf die Piloten und Passagiere die Gravitation und die (horizontale) Zentrifugalkraft , wobei hier die Masse des betrachteten Passagieres oder Piloten ist. Die zwei Kräfte addieren sich vektoriell in eine Resultierende, deren Richtung dem Auftrieb entgegengesetzt ist und den Flugzeuginsassen, unabhängig von der Querneigung des Flugzeuges, immer senkrecht in den Sitz drückt. Im Gegensatz zu Autofahrten werden Piloten und Passagiere selbst in sehr steilen Kurven nie vom Sitz seitlich weggedrückt.
Bahnstrecke Tuttlingen ....
| Tuttlingen–Inzigkofen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 Rechts ein mechanisches Einfahrvorsignal der Station Fridingen Zug beim Schanztunnel, Fahrt Richtung Beuron. Rechts ein mechanisches Einfahrvorsignal der Station Fridingen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Streckennummer: | 4660 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Kursbuchstrecke (DB): | 743 (Rottweil/Sigmaringen–Waldshut) 755 (Neustadt – Ulm) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Streckenlänge: | 37,1 km | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Spurweite: | 1435 mm (Normalspur) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Wirtschafliche Jagd

Bei der professionellen Jagd wird ein wirtschaftlicher Profit erzeugt. Berufsjäger, auch professioneller Jäger (englisch Professional hunter (PH)) genannt, kommen in verschiedensten Bereichen zum Einsatz. So zum Beispiel als Jagdführer, als Wildhüter oder als Jäger zur Beschaffung von Wildbret.
Bei der wirtschaftlichen Beschaffung von Fleich werden in einem begrenzten Gebiet in nur kurzer Zeit eine grosse Zahl von Tieren erlegt. Das erlegte Wild wird oft im Feld mit Hilfe einer mobilen Metzgerei/Schlachterei verarbeitet. Ein Kühllastwagen holt das Fleisch vor Ort im Feld ab. Diese Art der Fleischversorgung wird vor allem in Ländern mit langen Anfahrtswegen zur Schlachterei, wie zum Beispiel in Namibia oder Südafrika, angewandt.
Azimut der Sonne bei Sonnenaufgang

Das Azimut der aufgehenden Sonne hängt von der geographischen Breite des Beobachters und der momentanen Deklination der Sonne, also von der Jahreszeit ab.
Das Azimut der aufgehenden Sonne kann als Funktion der geographischen Breite des Beobachters und der Deklination der Sonne mit Hilfe der sphärischen Trigonometrie berechnet werden. Am 21. Juni (Sommeranfang auf der N-Halbkugel) steht die Sonne auf dem nördlichen Wendekreis und hat eine Deklination von 23,4° Nord. Am 23. September und am 20. März steht die Sonne auf dem Äquator und hat eine Deklination von 0°. Am 21. Dezember (Winteranfang für die N-Halbkugel) hat die Sonne eine Deklination von 23,4°S. Das Azimut der aufgehenden Sonne ist:
Die Berechnung des Azimutes des Sonnenaufganges zeigt unter anderem auch, dass bei Winteranfang auf z. B. 80° nördlicher Breite die Sonne nicht aufgeht. Für diese Breite und die gegebene Deklination von −23,4° hat das Azimut keinen reellen Wert.
Die Steilheit (Winkel ), mit der die Sonne bei Sonnenaufgang über den Horizont steigt, kann für die verschiedenen Breiten und die gegebene Deklination wie folgt berechnet werden:
Die Grafik rechts zeigt, das bei Sommerbeginn auf der nördlichen Hemisphäre (21. Juni) für einen Beobachter auf 60° nördlicher Breite die Sonne mit einem Azimut von 37° aufgeht und unter einem relativ flachen Winkel von 19° rechtsläufig über den Horizont steigt. Für einen Beobachter auf 20° Nord steigt die Sonne bei einem Azimut von 65° viel steiler, nämlich mit einem Winkel von 68° über den Horizont. Für diesen Beobachter läuft die im Nordosten aufgehende Sonne erst in Richtung Osten und im späteren Vormittag plötzlich gegen Norden. Für Beobachter am Äquator steigt die Sonne bei Sonnenaufgang das ganze Jahr senkrecht auf. Bei Frühling- und Herbstbeginn steigt die Sonne an jedem Ort der Erde mit einem Winkel über den Horizont. Zum Beispiel wird an diesen zwei Tagen auf 40° Breite die Sonne bei Sonnenaufgang mit einem Winkel von 50° über den Horizont steigen. Sowohl bei Sommer– wie auch Winteranfang wird die Sonne am gleichen Ort bei Sonnenaufgang mit einem Winkel von 45° aufsteigen.
Herleitung
Azimut bei Sonnenaufgang
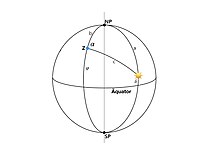

Zur Berechnung des Azimutes der Sonne bei Sonnenaufgang und zur Berechnung der Steilheit, mit der die Sonne bei Sonnenaufgang über den Horizont steigt betrachtet man das sphärische Dreieck, das mit den drei Punkten Nordpol, Zenit des Beobachters und Position der Sonne aufgespannt wird. In der Grafik bezeichnet Z den Zenit, NP den Nordpol, SP den Südpol. ist das Azimut der Sonne vom Beobachter aus gesehen. c ist die Zenitdistanz der Sonne vom Beobachter aus gesehen. ist die geographische Breite des Beobachters und ist die Deklination der Sonne.
Das aufgezeigte Dreieck wird mit dem sphärischen Seiten-Kosinussatz beschrieben:
Ersetzt man a, b und c mit , und , wobei h die Höhe der Sonne über dem Horizont ist, so folgt:
Bei Sonnenaufgang steht die Sonne auf der Höhe h=0° über dem Boden. Mit h=0° wird das Azimut der aufgehenden Sonne:
Steilheit des Sonnenaufganes
Bei Sonnenaufgang steigt die Sonne im Winkel über den Horizont. Es ist:
Die erste Ableitung von nach h an der Stelle h=0 eingesetzt ergibt:
Der Winkel ist positiv, wenn die Sonne von links nach rechts, also von Osten gegen Süden steigt. Läuft die im Osten aufgehende Sonne bei Sonnenaufgang von rechts nach links, also gegen Norden, so wird der Winkel negativ ausgedrückt.
Goageb

Goageb ist ein Ort an der Bahnstrecke Lüderitz–Seeheim in Namibia. Bei Goageb überquert die Bahn auf einer Stahlbrücke den Konkiep und in Goageb zweigt die Hauptstraße C14 von der Nationalstraße B4 nach Norden Richtung Bethanie ab. Der Ort ist heute (2018) eine Geisterstadt. Von der ehemaligen Bahnstation, der ehemaligen Tankstelle, vom ehemaligen Hotel und von der ehemaligen Kirche sind nur noch Ruinen übrig. Goageb ist heute unbewohnt.

Weblinks
Koordinaten: 26° 45′ S, 17° 14′ O
Berechnung der Dichtehöhe
Die oben aufgeführte Grafik zeigt, wie die Dichtehöhe ausgehend von der Druckhöhe (Pressure-Altitude) und der momentan herrschgenden Temperatur abgeleitet wird. Die Dichtehöhe verändert sich für jedes Grad der Abweichung von der Normtemperatur für die gegebene Drucköhe um 120 Fuss.[3] Die Druckhöhe ist die Höhe in der Standardatmosphäre, auf der derselbe Druck herrscht, wie am Ort unserer Betrachtung. Die Druckhöhe andert sich um 30 Fuss für jedes hPa Druckabweichung vom Normdruck auf Meereshöhe.[4] Zur Bestimmung der Dichtehöhe, muss erst die Druckhöhe (aus geografischer Höhe und Druckabweichung vom Normalduck) bestimmt werden. Anschliessend kann die Dichtehöhe (aus Druckhöhe und Abweichung von der Normtemeperatur) bestimmt werden.
- Die Druckhöhe kann, wenn ein Flugzeug am Boden steht, abgelesen werden, indem der Höhenmesser auf 29.92 inch Quecksilbersäule (= 1013 hPa) eingestellt wird.
- OAT, die Außenlufttemperatur in Grad Celsius
- Die ISA-Temperatur beträgt auf Meereshöhe 15 °C und sie sinkt pro 1000 Fuß Höhe um 2 °C. Auf 9000 Fuß Höhe beträgt die ISA-Temperatur also −3 °C.
Beispiel
Der Flugplatz von Samedan liegt auf 5600 Fuß bzw. 1707 m Höhe über Meer. Die Normtemperatur für diese Höhe ist 4 °C. Die momentande Temperatur sei 25 °C. Der Luftdruck auf Meereshöhe (QNH) betrage bei Samedan momentan 1000 hPa.
Der momentane Luftdruck liegt 13 hPa unter dem Normaldruck. Die Druckhöhe liegt damit über der geografischen Höhe. Die Druckhöhe ist damit . Die momentane Temperatur liegt 21°C über der Normtemperatur. Die Dichtehöhe liegt somit über der Druckhöhe. Die Dichtehöhe ist
Wirtschaft

Einige Gebiete der Kalahari liegen brach, in anderen wird Viehwirtschaft betrieben.[5] Insbesondere ist die Kalahari in Namibia flächendeckend in Farmen oder Herero-Stammgebiete eingeteilt. In der namibischen Kalahari werden vor allem Rinder, Schafe oder Wild gehalten. Von hier wird Fleisch nach Europa exportiert.[6] Auch für die Pferdezucht ist die Kalahari geeignet.[7] Ein bedeutender wirtschaftlicher Sektor bilden die Jagdfarmen. Ein weiterer wirtschaftlicher Zweig ist der Tourismus. Immer mehr Touristen werden von der Kalahari mit ihren langen, geraten Sanddünen und der hier vorhandenen Tiervielfalt angezogen. Im Okavangobecken ist Tourismus der einzige wirtschaftliche Zweig. In Salzseen wird „Kalahari-Salz“ gefördert, das als hochpreisiges Salz nach Nordamerika und Europa exportiert wird.[8]
Klippen
Markante und bekannte Klippen sind die Fingerklippe[9] und der Mukurob in Namibia. Die Fingerklippe zwischen Outjo und Khorixas ist eine Touristenattraktion. Der Mukurob im Süden Namibias ist am 7. Dezember 1988 eingestürzt.
Letzte Änderungen am Abschnitt Horizont in der Nautik, Kimmlinie
Im Abschnitt Horizont in der Nautik, Kimmlinie wird die Distanz zum Horizont berechnet.
In Bezug auf die heutige Version des Abschnittes:
- Es ist nicht nötig, die Höhe unter dem Wurzelzeichen auszuklammern. Es bringt nichts, eine Kette von Wurzeln, die alle dasselbe aussagen, hinzuschreiben.
- Das Einsetzen der numerischen Werte in der Kette der Wurzelzeichen macht den Abschnitt unübersichtlich.
- Es bringt nichts, verschiedene Krümmungsradien in die Formel einzustzen, weil diese verschiedenen Radien in der Konstante vor der Wurzel nur Unterschiede in der zweiten Stelle hinter dem Komma bringen.
- Die exakte Formel numerisch durchzurechnen bringt nichts, weil die Näherung mit eine sehr gute Näherung ist. Die durch die Lichtbrechung erzeugte Unsicherheit ist grösser, als der durch die Näherung erzeugte Fehler.
Horizont in der Nautik, Kimmlinie
Die Kimm ist die auf offenem Meer sichtbare Grenzlinie zwischen Wasser und Himmel. Auf sie beziehen sich Messungen von Höhenwinkeln, zum Beispiel mit einem Sextanten.
Wegen der Erdkrümmung – der mittlere Erdradius beträgt 6371 km, der Krümmungsradius der Erde liegt zwischen minimal 6334 km und 6400 km maximal – erscheint die Kimm umso tiefer unter dem mathematischen Horizont, je höher sich der Beobachter über dem Meeresspiegel befindet.
Daher müssen die Höhenwinkel um die Kimmtiefe verkleinert werden. Diese sogenannte Höhenbeschickung beträgt
(Kimmtiefe in Bogenminuten; Höhe des Beobachters in Metern).
Nach der DIN 13312 („Navigation; Begriffe, Abkürzungen …“) soll für die Kimmtiefe in der Seefahrt die Abkürzung „Kt“, im Englischen die Abkürzung „D“ (von dip of horizon), in der Luftfahrt die Abkürzung „Dip“ verwendet werden; als Formelzeichen wird für die Seefahrt k empfohlen.
Die Distanz des Horizonts von einem Punkt mit der Höhe über dem Meer ist:
Für Höhen , die sehr viel kleiner als der Erdradius sind , kann der Term gegenüber vernachlässigt werden[10]; damit wird
Mit dem mittleren Erdradius von wird die Distanz zum Horizont
Ein Beobachter auf einer Höhe von 400 Metern sieht den Horizont in einer Entfernung von 71 Kilometern.
Die geometrisch berechnete Distanz zum nautischen Horizont entspricht wegen der Lichtbrechung in der Erdatmosphäre nicht genau der Entfernung zum optischen Horizont. Abhängig von den Druck- und Temperaturbedingungen in der unteren Lufthülle kann die terrestrische Refraktion erheblich schwanken.
Die Sichtweite zum optischen Horizont liegt in einem Bereich:
- .
Im Beispiel mit einer Beobachtungshöhe von 400 Metern kann die Sichweite bis 78 Kilometer betragen.
Für Details und zusätzliche Beispiele siehe auch geodätische Sichtweite.
Die Distanz zum Horizont des Meeres


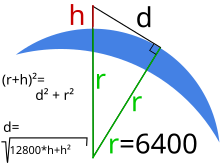
Auf Grund der Erkrümmung ist die Sichtweite über dem Meer begrenzt. Die Distanz zum Horizont hängt von der Augenhöhe des Beobachters über dem Meer ab. Mit dem Erdradius wird nach Pythagoras das im nebenstehend Bild abgebildete rechtwinklige Dreieck wie folgt beschrieben:
Für Höhen, die viel kleiner als der Erdradius sind , kann der Term vernachlässigt werden und es folgt:
Setzt man für den Erdradius R=6371 km ein, so folgt:
Der Fotograf des nebenstehenden Bildes stand bei der Aufnahme zirka neun Meter über dem Meer.[11] Der Horizont liegt somit in 11 km Distanz. Wegen der terrestrischen Refraktion kann die Sichtweite um einige Prozente vergrössert werden.
============================ Version 2
Auf Grund der Erkrümmung ist die Sicht über dem Meer begrenzt. Die Distanz zum Horizont hängt von der Augenhöhe des Beobachters über dem Meer ab.
Bei einer Augenhöhe des Beobachters von 2 Meter über dem Meeresspiegel liegt der nautische Horizont in rund 5,5 km Entfernung (mittlere terrestrische Refraktion berücksichtigt; zur Herleitung siehe Geodätische Sichtweite).
====== Für Seite Horizont:

Die Entfernung des Horizonts von einem Punkt mit der Höhe über der Erdoberfläche (Sichtweite) berechnet sich nach der Formel
wobei den Erdradius von 6371 km bezeichnet. Für Höhen , die viel kleiner als der Erdradius sind kann der Term gegenüber vernachlässigt werden und die Formel vereinfacht sich zu
Setzt man den angegeben Erdradius ein, so folgt:
Masseinheit:
Professionelle Jagd
Bei der professionellen Jagd geht es um die Gewinnung von Fleisch. Ein professioneller Jäger (englisch Professional hunter (PH)) erlegt in einem begrenzten Gebiet in nur kurzer Zeit eine grosse Zahl von Tieren. Das Fleisch wird oft im Feld mit Hilfe einer mobilen Metzgerei/Schlachterei verarbeitet. Ein Kühllastwagen holt das Fleisch vor Ort im Feld ab. Diese Art der Fleischversorgung wird vor allem in Ländern mit langen Anfahrwegen zur Schlachterei, wie zum Beispiel in Namibia oder Südafrika, angewandt.
Annotiertes Bild / Datumsgrenze
https://de.wikipedia.org/wiki/Vorlage:Annotiertes_Bild/Doku
https://de.wikipedia.org/wiki/Hilfe:Vorlagenprogrammierung#Funktion_time
Wochentag: Freitag
Aufruf Switch bei "Vorlage:Wochentag-Abkürzung": Vorlage:Wochentag-Abkürzung
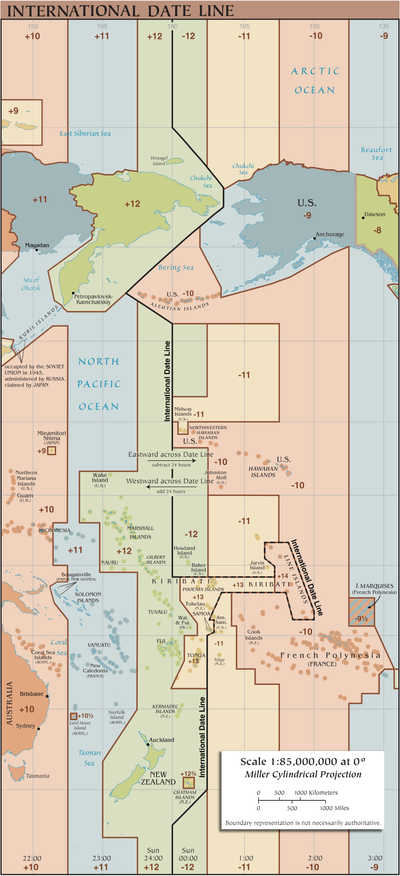
Die Karte rechts zeigt die Zeit- und Datumsverhältnisse in der Nähe der Datumsgrenze am 17. Januar 2025 um 21:10 Uhr UTC.
Täglich gibt es von 10:00 UTC bis 11:00 UTC auf der Erde, wie in Kapitel Karibati schon beschrieben, gleichzeitig drei verschiedene Kalenderdaten. Auf der Karte rechts sind die zwei Punkte, an denen die drei Daten während einer Stunde des Tages örtlich zusammenfallen, rot markiert.
Zeit in Namibia
Annotation Vorlage
Siehe: Benutzer:Hp.Baumeler/Anleitung Wikipedia#Annotations
Zeit
Siehe: Benutzer:Hp.Baumeler/Anleitung Wikipedia#Zeit-Aufrufe
Heliographen
Auch von der Schutztruppe in Deutsch-Südwestafrika (heute Namibia) wurden unter anderem in Halali, auf dem Dikwillem oder auf dem Klein Nauas Schutztruppenturm Heliographen eingesetzt, so bei der Niederschlagung des Herero-Aufstandes und im Ersten Weltkrieg. Die Übertragungsreichweite war über 70 km.
Hospiz in der Schweiz


In der Schweiz hat das Wort Hospiz zusätlich zu dem bis hierhin Beschriebenen die Bedeutung einer Herberge auf einem Alpenübergang. Hospize wurden früher meistens und zum Teil auch heute von Mönchen geführt. Hospize bieten Reisenden Unterkunft und Schutz vor harrschem Wetter, und sie sind seit jeher ein Ort der Begegnung. Das Hospiz auf dem Gotthardpass wurde bis 1841 von Kapuzinern geführt. Das Hospiz auf dem Simplonpass und das Hospiz auf dem Grossen St. Bernhard werden bis heute von den Augustiner-Chorherren geführt.
Bahnstrecke
| 13,2 | Donau | ||
---
| Swakopmund–Windhoek ursprünglicher Zustand 1902–1911 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Spurweite: | ursprünglich 600 mm umgespurt auf 1067 mm | ||||||||||||||||
| Maximale Neigung: | 45 ‰ | ||||||||||||||||
| |||||||||||||||||
---
| Swakopmund–Windhoek ursprünglicher Zustand 1902–1911 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Spurweite: | ursprünglich 600 mm umgespurt auf 1067 mm | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Maximale Neigung: | 45 ‰ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bahnwärterhaus
| Gotthard | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||
Sandskiing

So wie an Sanddünen das Skifahren auf Schnee nachgeahmt wird, so wird auf Sand auch das Wasserskifahren imitiert. Der Sportler lässt sich dabei von einem Fahrzeug auf Skiern oder auf alten Pneus über den Sand ziehen. Er stabilisiert seine Haltung, indem er sich wie beim Wasserskifahren an einem Zugseil hält und dabei zurücklehnt.
Jakalswater

Von der Bahnstation Jakalswater führte eine cirka xx km lange Schmalspurbahn bis zum Flussbett des Swakop, um von dort Wasser für die Dampflokomotiven nach Jakalswater bringen zu können. Das Trassee dieser von Nordwesten nach Südosten verlaufenden Zubringerbahn ist auf Satellitenfotos
![]()
![]()
![]() noch gut zu erkennen.
noch gut zu erkennen.
Niederschlagsmesser
Einfache analoge Niederschlagsmesser
......

Auf Farmen werden meist konische Regenmesser verwendet. Sie haben den Vorteil, dass kleine Regenmengen genauer als grosse Regenmengen abgelesen werden können. Die Markierungen bei kleinen Regenmengen liegen weiter auseinander als die Markierungen für grössere Regenmengen. Solche Regenmesser haben typisch eine Höhe von z.B. . Die Markierungsposition für die Regenmenge ist:
Mit einem konischen Regenmesser der Höhe kann maximal ein Niederschlag von
gemessen werden. Bei einem Regenmesser mit einer Höhe von 320 mm kann maximal eine Regenmenge von etwas über 100 mm erfasst werden.
Infobox deutsch-Wikipedia
|
Einleitung Lugano Bahnhof
Bisher
Der Bahnhof Lugano ist der einzige Bahnhof in der schweizerischen Stadt Lugano. Trotz des Namens Lugano-Paradiso befindet sich diese SBB-Haltestelle in der eigenständigen Gemeinde Paradiso. Der Bahnhof liegt an der Gotthardbahn und ist zudem Ausgangspunkt der meterspurigen Lugano-Ponte-Tresa-Bahn (FLP).
Neu
Der Bahnhof Lugano ist der Bahnhof der Schweizerischen Bundesbahnen in der Stadt Lugano. Der Bahnhof ist eine Station der Gotthardbahn. Er ist auch Ausgangspunkt der Lugano-Ponte-Tresa-Bahn (FLP) und Ausgangspunkt der TPL-Standseilbahn, die den Bahnhof mit dem tiefer gelegenen Stadtzentrum verbindet. Der Bahnhof Lugano ist der einzige Bahnhof der Stadt Lugano. Die SBB-Haltestelle mit dem Namen "Lugano-Paradiso" befindet sich in der eigenständigen Gemeinde Paradiso.
Nowrap
öahsf öadkh vödhv ösdhg vsöerfh öv oihdsöf hxcvhy.dyxbx,vdjc a.x vj bd,xvjb d,vn .kvn s.dvn s.vn .dv krgösdkfh vsrjdv dxmvy.10 kg (22 lb)
Sichtweite zum Horizont
Mit zunehmender Flughöhe rückt der aus dem Flugzeug beobachtete Horizont in immer grössere Entfernung. Fliegt ein Flugzeug über dem Meer oder über einem flachen Gebiet, wie zum Beispiel über der Kalahari, wird die Sichtweite wie folgt berechnet:
Hier muss die Flughöhe in Metern eingegeben werden. Die Distanz wird in Kilometern ausgedrückt. Fliegt ein Flugzeug in 900 Metern Höhe über flachem Grund, so liegt der Horizont in 108 Kilometern Entfernung. Dementsprechend ist die Sichtweite aus 10'000 Metern Höhe 360 Kilometer.
Getreidemühlen
Audio Datei
mit mini wird der TextText
Vorlage:Nowrap begin mit nowrap wird der TextText Vorlage:Nowrap end
mit nowrap 2 wird der TextText
Fließtext Fließtext
Mit Verweis isufhweors iufh osdb
aiufg asodch alsduch oiu  ylxdjhv ldjhvh l
ylxdjhv ldjhvh l
Aussprache von Trapani
nowrap:
texttext txttext
texttext etxttext
Zeitzonen

In der rechts abgebildeten Zeitzonenweltkarte ist der Umstand, dass Namibia ab Ende 2017 permanent zur Zeitzone UTC+2 gehört, berücksichtigt.
In der Kartenversion von 2016 ist Namibia der Zeitzone UTC+1 zugeordnet.
Infobox Bahnhof
| Simplon | |
|---|---|
 Bahnstation Simplon | |
| Daten | |
| Lage im Netz | Haltepunkt |
| Bahnsteiggleise | 1 |
| Eröffnung | 1907 |
| Lage | |
| Staat | Namibia |
| Koordinaten | 26° 49′ 29″ S, 17° 20′ 55″ O
|
| Höhe (SO) | 900 m |
| Eisenbahnstrecken | |
Gegenwart
Heute wird das Simplon Hospiz von Prior François und drei weiteren Chorherren geführt. Das Hospiz ist ein Haus der Begegnung und es bietet bis zu 100 Gästen Platz. Im Haus finden Exerzitien, Schullager und Kurse statt. Das Haus ist auch Ausgangspunkt für Wanderungen und Skitouren im Simplongebiet.
Gotthard Basistunnel
{{BS|ID|km|Name|Anmerkung|Höhe}}
{{BS2|ID1|ID2|km|Name|Anmerkung|Anmerkung rechtsbündig}}
{{BS3|ID1|ID2|ID3|km|Name|Anmerkung|Anmerkung rechtsbündig}}
https://de.wikipedia.org/wiki/Wikipedia:Formatvorlage_Bahnstrecke/Bilderkatalog
| Gotthard | |||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||
Ceneri
{{BS|ID|km|Name|Anmerkung|Höhe}}
{{BS2|ID1|ID2|km|Name|Anmerkung|Anmerkung rechtsbündig}}
{{BS3|ID1|ID2|ID3|km|Name|Anmerkung|Anmerkung rechtsbündig}}
| Ahstadt–Behlingen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Geographische Koordinaten
..... Siehe: Geographische Koordinaten#Darstellung von geographischen Koordinaten .....

Geografische Koordinaten werden in drei Formaten dargestellt. Traditionell werden sie im Sexagesimalsystem angegeben, d. h. 1 Grad ist unterteilt in sechzig Minuten, 1 Minute wiederum in 60 Sekunden (Beispiel: 46°14'06.70"N 8°0'55.60"O). Typographisch werden dabei die Minuten und Sekunden durch eine Prime bzw. Doppelprime bezeichnet. In der zweiten Darstellung werden die Minuten in dezimaler Form geschrieben, die Angabe von Sekunden erübrigt sich. 0.1' entsprechen hier 6.0". In der dritten Darstellung werden die Grade in dezimaler Form dargestellt. 0.1° entsprechen hier 6.0'. Über beliebig viele Nachkommastellen kann die gewünschte Genauigkeit erreicht werden.
Der Wertebereich der Breitengrade geht von 90°S bis 90°N und die Werte der Längengrade liegen zwischen 180°W und 180°O. Um Missverständnissen vorzubeugen, werden zum Beispiel in der Fliegerei die Breitengrade immer zweistellig und die Längengrade immer dreistellig geschrieben. In Standard Terminal Arrival Route wird ein Beispiel für den Anflug nach Zürich gezeigt. Der Wegpunkt AMIKI auf der Landeanflug-Karte rechts ist mit 47°34.4'N 009°02.3'O angegeben. Auch die Angabe der Winkelminuten (und wenn nötig die Angabe der Bogensekunden) wird hier zweistellig geschrieben.
In der Tabelle sind als Beispiel die Koordinaten eines historischen Gebäudes aufgeführt. Die drei angegebenen Koordinaten in den drei Schreibweisen beschreiben alle den gleich Punkt. In der Darstellung ist der Buchstaben "h" ein Platzhalter für die Angaben der Himmelsrichtung N-S,W-O. Oft wird auch in deutschen Texten anstelle des "O" für Osten ein "E" für "East" geschrieben. Die Angabe der Himmelsrichtung kann vor oder nach der Koordinatenangabe stehen. Die Buchstaben "d", "m" und "s" stehen für Grad (Degrees), Minuten und Sekunden.
| Darstellung | Beispiel | Beschreibung |
|---|---|---|
| hddd° mm' ss.ss" | N46°14'06.70" E008°00'55.60" | Angabe in Graden(°), Minuten('), Sekunden(") und Dezimalsekunden |
| hddd° mm.mmm' | N46°14.11182' E008°00.92670' | Angabe in Graden(°), Minuten(') und Dezimalminuten |
| hddd.ddddd° | N46.235197° E008.015445° | Angabe in Grad(°) und Dezimalgrad |
Gotthardbahn
....... Siehe: Gotthardbahn#Der frühe Bahnbetrieb .......
Der frühe Bahnbetrieb
Der grafische Fahrplan der Gotthardbahn
Der grafische Fahrplan der Gotthardbahn zeigt eine grosse Vielfalt an Informationen über materielle und vor allem auch betriebliche Aspekte der Gotthardbahn im Jahre 1899, also 17 Jahre nach der Eröffnung des Gotthardtunnels und nach der Fertigstellung der Gotthardbahn. Die Legende zu den Zeichen des Fahrplanes und die Beschriftung der einzelnen Spalten befindet sich im Fahrplan ganz oben. Von links nach rechts informiert uns der Fahrplan über die Höhe der Stationen über Meer, das Längenprofil, die Signalanlagen, die Tunnels und deren Länge, das grösste Gefälle und die grösste Steigung bei Fahrten Richtung Süden auf den einzelnen Streckenabschnitten, die Kilometrierung der Bahn, die eingesetzten Telegraphen und deren Verbund, die Läutewerke und deren Verbund, das Streckentelefon, die Blockstationen, das Geleisebild der Stationsanlagen, die Stationsausrüstung, die totale „nützbare“ Länge der übrigen Geleise, das längste Ausweichgeleise, die Stationsnamen, die Entfernung von Station zu Station, die Entfernung vom Anfangspunkt, die Entfernung zwischen den Hauptstationen sowie die Ankunfts- und Abfahrtszeiten der Züge, wobei letztere in der Form eines grafischen Fahrplanes dargestellt sind.
Zum Beispiel sieht man, dass der Scheitelpunkt des Gotthardtunnels auf 1154.5 Meter über Meer liegt und dass der Tunnel nicht eine gerade Röhre ist, sondern von seinem Scheitelpunkt auf beide Seiten hin ein Gefälle aufweist. Der Tunnel wurde so gebaut, damit eindringendes Wasser abfliessen kann. Von Göschenen bis zum Scheitelpunkt steigt das Geleise mit 6 ‰ und vom Scheitelpunkt bis Airolo hat der Tunnel ein Gefälle von 2 ‰. Die Tunnellänge wird mit 14'998 Metern angegeben. Der Scheitelpunkt liegt bei Kilometer 80. Hier ist zu berücksichtigen, dass die Kilometrierung der alten Gotthardbahn, wie auf dem grafischen Fahrplan gut ersichtlich, bei Immensee begann.
Rechts von der Kilometrierung sind die Schreibtelegrafen und die Läutewerke aufgeführt, die in den Kapiteln Das Schreibtelegrafen-Netzwerk der Gotthardbahn und Das Läutewerk der Gotthardbahn beschrieben werden.


Die Geleisebilder der einzelnen Stationen zeigen, dass die Gotthardbahn im Jahr 1899 von Flüelen bis Giubiasco durchgehend zweispurig war. Das rechts stehende historische Bild des Bahnwärterhäuschens bei der Mondasciabrücke zeigt das doppelspurige Geleise und auch das Vorsignal des auf dem Fahrplan festgehaltenen Einfahrsignales (bei Kilometrierung 132.5) vor Biasca in nördlicher Fahrtrichtung.
Das rechts stehende Bild zeigt den Pianotondoviadukt und das obere Portal des Pianotondo-Kehrtunnels mit dem davorstehenden Bahnwärterhäuschen, es wurde zur Zeit des doppelspurigen Dampfbetriebes aufgenommen, also etwa um die Zeit, in der der grafische Fahrplan seine Gültigkeit hatte. Auf dem grafischen Fahrplan verlassen bei der Station Giubiasco zwei Geleise den Bahnhof in südlicher Richtung. Ein Geleise ist mit Chiasso und das andere mit Luino/Locarno angeschrieben. Ab hier sind die Strecken einspurig. Die südlichen Nachbarstationen von Giubiasco, nämlich Rivera-Bironico und Cadenazzo sind nur eingeleisig. Noch heute ist zum Beispiel an der Ceneri-Strecke bei jeder Bahnunterführung gut ersichtlich, dass die Unterführungen an zwei zeitlich weit auseinanderliegenden Zeitpunkten gebaut wurden. Die Strecken Giubiasco-Al Sasso und Al Sasso-Rivera wurden 1922 respektive 1934 auf Doppelspur ausgebaut.[12]
Der grafische Fahrplan ist eine zweidimensionale Darstellung der Zugfahrten. Auf der Horizontalen ist die Zeit von XII-Uhr (zwölf Uhr) Mitternacht bis wieder XII-Uhr Mitternacht aufgeführt. In der Vertikalen sind die Bahnhöfe von Zug und Luzern bis Chiasso, Locarno und Luino dargestellt. Ein erster nicht „facultativer“ Zug verlässt Bellinzona um 03:17 Uhr in der Nacht. Dies ist ein Schnellzug mit I., II. und III.-Klasse. Zug Nummer 55 wird von einer Dampflokomotive gezogen. Bei den Stationen Giubiasco, Rivera-Bironico und Taverne ist kein Aufenthalt vorgesehen. Die Ankunftszeit in Lugano ist um 04:09 Uhr und die dortige Abfahrtszeit nach fünf Minuten Aufenthalt um 04:14 Uhr. Im Jahr 1899 betrug die Fahrzeit von Bellinzona bis Lugano im Schnellzug genau 52 Minuten. Die EuroCity fahren heute (2017) dieselbe Strecke in 27 Minuten. In der Grafik sieht man, dass sich auf der Strecke Giubiasco-Rivera Bironico keine Züge kreuzen, dies deshalb, weil es sich hier im Jahre 1899, wie oben erwähnt, um eine Einspurstrecke handelt. Dass Giubiasco-Rivera Bironico zu diesem Zeitpunkt eine Einspurstrecke war, erkennt man also einerseits aus dem Geleisebild der Bahnhöfe und andererseits aus dem grafischen Fahrplan. Auf der zweispurigen Strecke Osogna-Biasca gibt es immer wieder Züge, die sich auf der Strecke und somit auf dem grafischen Fahrplan kreuzen. Ein weiteres Detail ist, dass auf dem Fahrplan der Gotthardbahn auch die Züge der Arth-Rigi-Bahn, heute Rigi Bahnen, eingetragen sind. Der Massstab des Fahrplanes ist in der Horizontalen 15 Millimeter pro Stunde und in der Vertikalen 1.75 Millimeter pro Kilometer.
Das Schreibtelegrafen-Netzwerk der Gotthardbahn

Die Gotthardbahn unterhielt zur Koordinierung der Züge ein Schreibtelegrafen-Netzwerk, welches auf der gesamten Strecke von Luzern bis Chiasso, Locarno und Luino alle Bahnhöfe miteinander verband. Das Netzwerk der Schreibtelegrafen ist am linken Rande des grafischen Fahrplanes aus dem Jahre 1899 dargestellt. Die einzelnen Telegrafen sind für jede Station mit einem kleinen schwarzen Punkt markiert. Wie der Ausschnitt des Fahrplanes zeigt, hatte der Bahnhof Biasca zu jener Zeit vier Telegrafen in Betrieb. Einer dieser Telegrafen war mit allen Stationen von Biasca bis Bellinzona verbunden. Was auf diesem Telegrafen getastet (gemorst) wurde, konnte somit auf allen Stationen bis Bellinzona gelesen werden. Ein zweiter Telegraf war mit allen Stationen von Biasca bis Göschenen verbunden. Was auf dem dritten Telegrafen getastet wurde, konnte nur auf den Stationen Bellinzona, Faido, Airolo, Göschenen, Wassen und Erstfeld gelesen werden. Der vierte Telegraf war der Langstrecken-Apparat. Was auf ihm getastet wurde, konnte in Bellinzona, Airolo, Erstfeld, Goldau und Luzern gelesen werden. Die Schreibtelegrafen mit ihren Morse-Tasten und die Telegrafen-Relais wurden von der Hasler AG (Bern) hergestellt.
Das Läutewerk der Gotthardbahn

Die Gotthardbahn betrieb Läutewerke auf den Bahnhöfen und auf der Strecke. Die Läutewerke kündeten das Nahen eines Zuges an. Das Signal wurde ausgelöst, wenn ein Zug den benachbarten Bahnhof oder die benachbarte Blockstelle verliess. Zum Teil waren Läutewerke auf offener Strecke installiert. Diese Läutewerke warnten Bahnarbeiter vor dem Nahen eines Zuges. Zudem verfügte jedes Bahnwärterhaus und jedes Schrankenwärter-Haus über ein Läutewerk. Bei der Gotthardbahn wurde ein in Richtung Süden fahrender Zug mit drei mal drei Schlägen und ein in Richtung Norden fahrender Zug mit zwei mal zwei Schlägen angekündigt. Die Stationsbeamten, Streckenwärter und Bahnarbeiter mussten die Läutewerke täglich von Hand aufziehen. Dabei wurde im Läutewerk ein Gewicht an einem Flaschenzug hochgezogen. Das das Signal auslösende elektrische Signal betätigte im Läutewerk ein Relais, das einen mechanischen Vorgang auslöste, bei dem mit der Kraft des erwähnten Gewichtes der Hammer der Glocke hochgezogen wurde. Jedes einzelne Läutewerk der Gotthardbahn ist auf dem grafischen Fahrplan eingezeichnet. Als Beispiel wird im Ausschnitt des Fahrplanes das Läutewerk des Casello 159 (Bahnwärterhaus 159) an der Monte Ceneri-Strecke zwischen Giubiasco und Rivera-Bironico aufgezeigt. Wenn ein Zug den Bahnhof Giubiasco Richtung Süden verliess, ertönten auf der elf Kilometer langen Bahnstrecke bis Rivera-Bironico elf Läutewerke. Die Läutewerke an der Gotthardbahn wurden circa 1980 ausser Betrieb genommen.
Der Geleiseunterhalt und die Geleisesicherung

In den Jahren der frühen Gotthardbahn konnten Eisenbahnschienen noch nicht mit Ultraschall überprüft werden. Schienenbrüche waren zu jener Zeit daher weit häufiger als in der heutigen Zeit, in der die Geleise mit Ultraschallprüfzügen getestet werden können. Um den Betrieb der Gotthardbahn sicher zu stellen, kam dem Streckenwärter eine besondere Stellung zu. Er musste einen ihm zugeteilten Abschnitt einer Strecke täglich überprüfen. Die Aufgabe des Streckenwärters war, Schienenbrüche und Schienenverformungen zu erkennen und den Bahnmeister über den Zustand des Geleiseabschnittes zu informieren. Sie mussten aber auch lose Schrauben anziehen, Büsche zurückschneiden oder kleine Feuer löschen. Bei talwärts fahrenden schweren Güterzügen sprühten die Bremsklötze Funken und sehr oft entzündete sich damit das dürre Gras seitlich der Geleise. Der Bahnwärter war mit einer roten Flagge ausgerüstet, um Züge im Notfall zu stoppen. Die Streckenwärter wohnten entlang der Gotthardbahn in Bahnwärterhäuschen. Diese werden im Tessin Casello[13]genannt. Die Streckenwärter überprüften täglich den Geleiseabschnitt bis zum benachbarten Wärterhaus. Die einzelnen Bahnwärterhäuser lagen an der Gotthardstrecke in einem Bereich von zwei bis vier Kilometer auseinander und sie waren auf der gesamten Strecke durchnummeriert. In späteren Jahren, etwa ab 1950, mussten die Geleise weniger intensiv überwacht werden. Eine Strecke wie zum Beispiel Giubiasco-Rivera wurde dann nur noch jeden zweiten Tag von einem Streckenwärter abmarschiert. Ab diesem Zeitpunkt standen viele Bahnwärterhäuser leer oder sie wurden als Ferienhaus oder als Wohnhaus von Privatpersonen benutzt. Ab 1995 begannen die SBB, die Bahnwärterhäuschen zu verkaufen.
..... Siehe Gotthardbahn#DoppelspurTabelle .....
| Ausbau der Gotthardbahn auf Doppelspur[14] | |
|---|---|
| Teilstrecke | Eröffnung der Doppelspur |
| Immensee — Brunnen | 01.05.1904 |
| Brunnen — Sisikon | 15.09.1947 |
| Sisikon — Flüelen | 01.03.1943 |
| Flüelen — Altdorf | 15.01.1896 |
| Altdorf — Erstfeld | 06.12.1896 |
| Erstfeld — Silenen Amsteg | 09.04.1893 |
| Silenen Amsteg — Gurtnellen | 14.05.1893 |
| Gurtnellen — Wassen | 26.06.1892 |
| Wassen — Göschenen | 28.05.1893 |
| Göschenen — Airolo | 01.06.1883 |
| Airolo — Ambri Piotta | 02.09.1890 |
| Ambri Piotta — Rodi Fiesso | 31.07.1890 |
| Rodi Fiesso — Faido | 28.05.1890 |
| Faido — Lavorgo | 13.09.1891 |
| Lavorgo — Giornico | 27.03.1892 |
| Giornico — Bodio | 01.05.1892 |
| Bodio — Biasca | 15.05.1892 |
| Biasca — Osogna | 31.05.1896 |
| Osognia — Bellinzona | 19.04.1896 |
| Bellinzona — Giubiasco | 01.06.1883 |
| Giubiasco — Al Sasso | 20.12.1922 |
| Al Sasso — Rivera Bironico | 21.01.1934 |
| Rivera Bironico — Mezzovico | 27.03.1942 |
| Mezzovico — Taverne Torricella | 02.05.1946 |
| Taverne Torricella — Lugano | 30.04.1942 |
| Lugano — Melide | 10.10.1915 |
| Melide — Bissone | 02.04.1965 |
| Bissone — Maroggia Melano | 03.06.1956 |
| Maroggia Melano — Mendrisio | 01.10.1913 |
| Mendrisio — Chiasso | 01.05.1912 |
- ↑ Die Funkstation Aus: Der Erste Weltkrieg im Schutzgebiet S.253
- ↑ a b Das in der Grafik verwendete Flugzeugsymbol wurde dem Icon Airplane-from-behind.svg entnommen
- ↑ Density Altitude. In: AOPA. Abgerufen am 7. August 2018.
- ↑ Siehe die englische Wikipediaseite Pressure altitude
- ↑ Philip’s College Atlas for Southern Africa. George Philip & Son, London 1976, ISBN 0-540-05320-1, S. 12.
- ↑ Siehe zum Beispiel: Meatco
- ↑ Siehe zum Beispiel: Dunside Stud
- ↑ Eintrag bei lebensmittellexikon.de, abgerufen am 1. August 2014
- ↑ Namibia Travel Map. Kunth-Verlag, München 2017, ISBN 978-3-95504-578-4.
- ↑ Selbst für ein auf 10 km Höhe fliegendes Flugzeug ist
- ↑ Der Fotograf stand auf der Jetty in Swakopmund
- ↑ Gotthardbahn Luzern / Zug – Chiasso
- ↑ siehe it:Casello ferroviario in der italienischsprachigen wikipedia
- ↑ Der Ausbau auf Doppelspur. Abgerufen am 23. August 2017.






























![{\displaystyle \alpha (d)=180^{\circ }-\operatorname {arccot} \left[{\frac {{\frac {\sin \varphi _{1}\cdot \sin \delta }{\cos \varphi _{1}}}-\cos \delta \cos \alpha _{0}}{\sin \alpha _{0}}}\right]\qquad {\mbox{wobei}}\qquad \delta ={\frac {d(km)}{1.852{\frac {km}{'}}\cdot 60'}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfb1f7b912a038813ebbcab9ccdb2d4929d4ac1f)
![{\displaystyle \alpha (d)=180^{\circ }-\operatorname {arccot} \left[{\frac {\sin \varphi _{1}\cdot \sin \delta }{\cos \varphi _{1}\cdot \sin \alpha _{0}}}-{\frac {\cos \delta }{\tan \alpha _{0}}}\right]\qquad {\mbox{wobei}}\qquad \delta ={\frac {d(km)}{1.852{\frac {km}{'}}\cdot 60'}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e4965fff0611180e44005069927cf60cab1559e)































![{\displaystyle \alpha _{SR}=\arccos \left[{\frac {\sin(\delta )}{\cos(\varphi )}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2aab3dccd3308333ff767e0be2f72edacae4512e)
![{\displaystyle \beta =\arctan \left[\cot(\varphi ){\sqrt {1-\sin ^{2}(\delta )\sec ^{2}(\varphi )}}\right]=\arctan \left[{\frac {\sin(\alpha _{SR})}{\tan(\varphi )}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/591f21b9afc9d10e3242d866a2f259fb931e65cf)


![{\displaystyle \cos \alpha ={\frac {\cos[a]-\cos[b]\cos[c]}{\sin[b]\sin[c]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaba4bd4c33eb8b1742b1f8b958d2bf3546d3816)



![{\displaystyle \alpha =\arccos[\sec(h)\sec(\varphi )(\sin(\delta )-\sin(h)\sin(\varphi ))]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb190efeba524af8b1f7b61b70509c6522fc1e69)

![{\displaystyle \tan(\beta )=\left[\cot(\varphi ){\sqrt {1-\sin ^{2}(\delta )\sec ^{2}(\varphi )}}\right]={\frac {\sin(\alpha _{SR})}{\tan(\varphi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/460123eb5d4f6e665b5fc0ffee57e3c686a25681)







































![{\displaystyle x={\sqrt[{3}]{3hH^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53141cb3e5391d5c2b7e1f15ebb73c3dca380e59)






