Ormelignende kæde

Den ormelignende kæde (engelsk: worm-like chain (WLC)) er en matematisk model, der beskriver en relativt stiv polymers konformationer.^[1]

Modellen

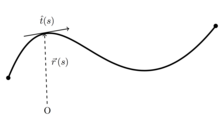
I modellen beskrives en polymer som en linje, hvor hvert punkt $s$ langs polymeren har en position i rummet samt en tangentiel vektor ${\vec {t}}(s)$ , der angiver linjens orientering i det punkt. I et andet punkt $u$ har linjen også en orientering ${\vec {t}}(u)$ ; da polymeren er stiv, vil orienteringerne være stortset ens, hvis $u$ er tæt på $s$ , mens orienteringerne er fuldstændigt ukorrelerede, hvis $u$ er langt på $s$ . For et gennemsnit af alle mulige konformationer vil prikproduktet mellem de to tangentielle vektorer altså være henholdsvis 1 og 0:

\langle {\vec {t}}(s)\cdot {\vec {t}}(u)\rangle =\left\{{\begin{matrix}1&{\mbox{for }}|u-s|=0\\0&{\mbox{       for }}|u-s|\rightarrow \infty \end{matrix}}\right.

Dette er korrelationsfunktionen, og det antages, at faldet fra 1 til 0 er eksponentielt:

\langle {\vec {t}}(s)\cdot {\vec {t}}(u)\rangle =\mathrm {e} ^{-{\frac {|u-s|}{l_{\mathrm {p} }}}}

hvor $l_{\mathrm {p} }$ er persistenslængden, der er den karakteristiske afstand for korrelationen mellem to punkter i polymeren. Det ses, at stivere polymere har større persistenslængder.

Den samlede vektor ${\vec {R}}$ fra den ene ende af polymeren til den anden er blot givet ved integralet langs hele polymerens kædelængde $L$ :

{\vec {R}}=\int _{0}^{L}{\vec {t}}(s)\mathrm {d} s

Fordi den samlede polymer kan være orienteret i en hvilken som helst retning, er gennemsnittet af ${\vec {R}}$ lig med nul. For at finde et mål for polymerens udstrækning benyttes i stedet den gennemsnitlige kvadrerede værdi, da den ikke kan være negativ:

\langle {\vec {R}}^{2}\rangle =\left\langle \left(\int _{0}^{L}{\vec {t}}(s)\mathrm {d} s\right)\cdot \left(\int _{0}^{L}{\vec {t}}(u)\mathrm {d} u\right)\right\rangle =\left\langle \int _{0}^{L}\int _{0}^{L}{\vec {t}}(s)\cdot {\vec {t}}(u)\mathrm {d} s\mathrm {d} u\right\rangle =\int _{0}^{L}\int _{0}^{L}\langle {\vec {t}}(s)\cdot {\vec {t}}(u)\rangle \mathrm {d} s\mathrm {d} u=\int _{0}^{L}\int _{0}^{L}\mathrm {e} ^{-{\frac {|u-s|}{l_{\mathrm {p} }}}}\mathrm {d} s\mathrm {d} u

Pga. den absolutte værdi kan integralerne skrives som

\langle {\vec {R}}^{2}\rangle =2\int _{0}^{L}\int _{u}^{L}\mathrm {e} ^{-{\frac {|u-s|}{l_{\mathrm {p} }}}}\mathrm {d} s\mathrm {d} u=2\int _{0}^{L}\int _{0}^{L-u}\mathrm {e} ^{-{\frac {x}{l_{\mathrm {p} }}}}\mathrm {d} x\mathrm {d} u

hvilket giver:

\langle {\vec {R}}^{2}\rangle =2\int _{0}^{L}\left[-l_{\mathrm {p} }\mathrm {e} ^{-{\frac {x}{l_{\mathrm {p} }}}}\right]_{0}^{L-u}\mathrm {d} u=2l_{\mathrm {p} }\int _{0}^{L}\left(1-\mathrm {e} ^{-{\frac {L}{l_{\mathrm {p} }}}}\mathrm {e} ^{\frac {u}{l_{\mathrm {p} }}}\right)\mathrm {d} u=2l_{\mathrm {p} }\left(L-l_{\mathrm {p} }\mathrm {e} ^{-{\frac {L}{l_{\mathrm {p} }}}}\left(\mathrm {e} ^{\frac {L}{l_{\mathrm {p} }}}-1\right)\right)=2l_{\mathrm {p} }L\left(1-{\frac {l_{\mathrm {p} }}{L}}\left(1-\mathrm {e} ^{-{\frac {L}{l_{\mathrm {p} }}}}\right)\right)

Hvis kædelængden er meget større end persistenslængden, reducerer udtrykket til:

\langle {\vec {R}}^{2}\rangle =2l_{\mathrm {p} }L

hvilket vil sige, at root-mean-square-længden er:

${\sqrt {\langle {\vec {R}}^{2}\rangle }}={\sqrt {2l_{\mathrm {p} }L}}$

Det ses, at polymerens udstrækning vokser med kvadratroden af kædelængden. Dvs at lange polymerer har tendens til at krølle sig sammen; denne tilstand kaldes for en polymer coil. Det ses desuden, at skaleringsloven minder om den ideelle kæde

{\sqrt {\langle {\vec {R}}^{2}\rangle }}={\sqrt {aL}}

hvor $a$ er længden af hvert enkelt led i den ideelle kæde. Ved sammenligning ses det, at den ormelignende kæde har samme størrelse som den ideele kæde, hvis

a=2l_{\mathrm {p} }

Denne længde kaldes for Kuhn-længden, og for den ormelignende kæde er Kuhn-længden altså lig med den dobbelte persistenslængde.

Tilsvarende er gyrationsradiussen $R_{\mathrm {G} }$ derfor givet ved:

R_{\mathrm {G} }={\sqrt {\frac {aL}{6}}}={\sqrt {\frac {l_{\mathrm {p} }L}{3}}}

Den gennemsnitlige afstand til massemidtpunktet stiger altså også med kvadratroden af kædelængden.^[1]

Kildehenvisninger

^ ^a ^b ^c Phillips, Rob; Kondev, Jane; Theriot, Julie; Garcia, Hernan G. (2003). "Ch. 8 - Random Walks and the Structure of Macromolecules". Physical Biology of the Cell (engelsk) (2. udgave). Garland Science. s. 319-321. ISBN 978-0-8153-4450-6.

[phillips_319-1] Phillips, Rob; Kondev, Jane; Theriot, Julie; Garcia, Hernan G. (2003). "Ch. 8 - Random Walks and the Structure of Macromolecules". Physical Biology of the Cell (engelsk) (2. udgave). Garland Science. s. 319-321. ISBN 978-0-8153-4450-6.

[1]

Fahrer / Team für die Suche eingeben:

Fahrer / Team für die Suche eingeben:

Langbahn Team – Weltmeisterschaft

Ormelignende kæde

Modellen

Kildehenvisninger