Naturtone
Naturtoner er de toner, man kan frembringe på en messingblæser uden brug af ventiler eller lignende hjælpemidler. Tonerne fremkommer ved at tvinge luftsøjlen til at svinge dobbelt så hurtig, tre gange så hurtig osv. På et jagthorn kan der kun spilles naturtoner. Der er stor afstand mellem de dybeste naturtoner, mens de høje ligger tættere og tættere.
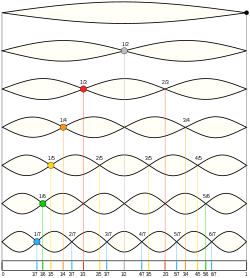
Man kan også frembringe naturtonerne på en udspændt streng. Normalt vil den svinge med en bestemt frekvens, men hvis man fx deler den på midten med en forsigtig finger, vil hver af strengens to halvdele svinge dobbelt så hurtig. På samme måde kan man tredele den (en forsigtig finger en tredjedel inde), så de tre tredjedele vil svinge med tredobbelte frekvens, osv.
Den dybeste tone hedder grundtonen, de højere naturtoner overtoner eller partialtoner. På de fleste instrumenter vil man altid sammen med grundtonen kunne høre nogle af overtonerne. Tilsammen danner alle de hørlige toner instrumentets klang.
Ud fra grundtonen C, bliver de første naturtoner:
- 1: C (66 Hz). Grundtonen. Man kalder intervallet fra grundtonen til grundtonen en prim.
- 2: c (132 Hz). Intervallet fra 1. til 2. naturtone kaldes en oktav. De to toner opfattes som den samme, blot i et andet leje. Fx vil en voksen mand og en voksen kvinde ofte synge en melodi sammen med en oktavs forskel. Ved en oktav multipliceres frekvensen med 2.
- 3: g (198 Hz). Intervallet fra 2. til 3. naturtone kaldes en kvint. Det opfattes som et meget rent interval, som det er meget nemt at stemme et instrument efter ved hørelsen. Frekvensen multipliceres med 3/2 = 1,5.
- 4: c1 (264 Hz). Intervallet fra 3. til 4. naturtone kaldes en kvart, og det opfattes ligesom en kvint som et rent interval. Frekvensen multipliceres med 4/3 = 1,3333... Intervallet fra 2. til 4. naturtone er (ligesom fra 1. til 2.) en oktav, hvor frekvensen multipliceres med 2.
- 5: e1 (330 Hz). Intervallet fra 4. til 5. naturtone kaldes en stor terts. Det er et afgørende interval i en durskala. Frekvensen multipliceres med 5/4 = 1,25.
- 6: g1 (396 Hz). Intervallet fra 5. til 6. tone kaldes en lille terts, som er et afgørende interval i en molskala. Frekvensen multipliceres med 6/5 = 1,2. Intervallet fra 4. til 6. naturtone er (ligesom fra 2. til 3.) en kvint, hvor frekvensen multipliceres med 3/2. Intervallet fra 3. til 6. naturtone er en oktav.
- 7: Et lavt b1 (462 Hz). Den 7. naturtone opfattes som falsk i de mest anvendte skalaer, men intervallet fra 4. til 7. grundtone ligger tæt på det interval, som kaldes en lille septim.
- 8: c2 (528 Hz). Intervallet fra 6. til 8. naturtone er også en kvart, hvor frekvensen multipliceres med 4/3 = 1,3333... Intervallet fra 4. til 8. grundtone er en oktav.
- 9: d2 (594 Hz). Intervallet fra 8. til 9. naturtone kaldes en (stor) sekund, som også kaldes en heltone. Frekvensen multipliceres med 9/8 = 1,125. Intervallet fra 6. til 9. naturtone er en kvint. En sekund findes altså ved fra en given tone at gå to kvinter op og en oktav ned (eller en kvint op og en kvart ned).
Stemninger
Ovenstående oversigt over naturtonerækken viser, hvordan centrale intervaller forekommer naturligt. Det gælder de rene intervaller oktav, kvint og kvart gennem de fire første naturtoner. Derudover finder man gennem de to næste naturtoner intervallerne stor terts og lille terts, som bruges til at farve musikken. Endelig findes intervallet sekund gennem den 9. grundtone, som desuden har den egenskab, at den kan fremkaldes ved hjælp af de rene intervaller (oktav, kvint og kvart).
Pythagoræisk stemning


Disse sammenhænge kendte man allerede i antikken, og den pythagoræiske skole tillægges ofte opdagelsen af dem. Op igennem middelalderen anvendte man de rene intervaller til at stemme instrumenterne, og dette kalder man i dag pythagoræisk stemning. I denne stemmer man vha. kvintcirklen, idet man ud fra grundtonen stemmer den næste tone en kvint op (og evt. en oktav ned, dvs. alt i alt en kvart ned). Med udgangspunkt i tonen F er den næste tone et C (der både er en kvint over og en kvart under). Den næste tone er et G, som netop er en sekund (med faktor 9/8) over F. Dette interval kalder man en heltone. På den måde fyldes mellemrummene mellem F'et og C'et ud med heltoner, indtil de "møder" hinanden, og man får fremstillet følgende diatoniske skala med i alt 7 forskellige toner:
| Rækkefølge i 'kvintcirklen' (F = 1) | Tone | Frekvens, faktor i forhold til C |
|---|---|---|
| 2 | C | 1 |
| 4 | D | 9/8 = 1,125 |
| 6 | E | 81/64 = 1,2656... |
| 1 | F | 4/3 = 1,3333... |
| 3 | G | 3/2 = 1,5 |
| 5 | A | 27/16 = 1,6875 |
| 7 | H | 243/128 = 1,8984... |
| 2 | C | 2 |
Den diatoniske skala er grundlaget i den vestlige verdens musik, og dens udgangspunkt var altså oprindeligt de naturlige rene intervaller oktav, kvint og kvart. Desuden er en heltone også et naturligt interval, nemlig intervallet fra den. 8. til den 9. naturtone med faktoren 9/8 = 1,125. I den pythagoræiske stemning kommer der således 5 steder en heltone. De to sidste steder, fra E til F og fra H til C, er der et interval med en faktor på 256/243 ≈ 1,05350, og dette interval kalder man en diatonisk halvtone (i den pythagoræiske stemning). De 5 mellemrum i heltonerne kan herefter videre fyldes ud med halvtoner, som enten bliver forsænkede toner (Bb, Eb, Ab, Db, Gb), hvis man går fra F og baglæns i kvintcirklen, eller hævede toner (F# ≈ Gb, C# ≈ Db, G# ≈ Ab, D# ≈ Eb, A# ≈ Bb), hvis man går fra H og forlæns i kvintcirklen. Her må vælge, hvilke af halvtonerne, man vil stemme "oppefra" (med b) eller "nedefra" (med #). Intervallet fra en heltone til dens forsænkede eller hævede halvtone kaldes en kromatisk halvtone (i den pythagoræiske stemning), og den har en faktor på 2187/2048 ≈ 1,06787. Halvtonerne mellem heltonerne vil altså komme til at ligge forskelligt afhængigt af, hvilken stemning man vælger.
Forskellen skyldes, at 12 kvinter op justeret med 7 oktaver ned ikke giver 1, men (3/2)^12 : 2^7 = 3^12/2^19 ≈ 1,01364. Denne forskel finder man også som forholdet mellem faktorerne for den kromatiske halvtone og den diatoniske halvtone. Forskellen kaldes et pythagoræisk komma og er årsag til, at man må vælge mindst en af kvinterne i kvintcirklen til at være uren, den såkaldte ulvekvint. Det betyder ikke så meget for en akkord, at et interval på en halv tone ikke er ens hver gang, fordi de i forvejen kun indgår i en dissonans. Derimod er det vigtigt, at en kvint er ren. Resultatet er, at man ikke kan bruge en akkord i en melodi, hvis ulvekvinten indgår.
Den pythagoræiske stemning har også det problem, at den store terts er for stor. I følge den 5. naturtone skulle faktoren være 5/4 = 1,25 i stedet for 81/64 ≈ 1,2656, og tertsen vil lyde lidt falsk. Når man udelukkende stemmer vha. de rene intervaller, bliver det altså på bekostning af, at tertserne ikke stemmer. Denne forskel på (81/64) : (5/4) = 81/80 = 1,0125 kaldes et syntonisk komma, og den giver en hørlig urenhed.
Ren stemning
I nyere tid har man ønsket at have rene store tertser, og man er gået over til en såkaldt ren stemning, hvor det er sikret, at akkorderne tonika (i C-dur-skalaen tonerne C, E og G), dominant (tonerne G, H og D) og subdominant (tonerne F, A og C) er rene. Det gør man ved at stemme F, C, G og D på samme måde som i pythagoræisk stemning, men i stedet for at stemme A som en ren kvint oven på D, stemmes den som en ren stor terts oven på F. Herefter stemmes E, H og F# videre fra A i kvintcirklen. Det giver følgende diatoniske skala (suppleret med tritonus, F#).
| Rækkefølge i 'kvintcirklen' | Tone | Frekvens, faktor i forhold til C |
|---|---|---|
| …… 0 | C | 1 |
| ……………… 2 | D | 9/8 = 1,125 |
| ………………………… 4 | E | 5/4 = 1,25 |
| -1 | F | 4/3 = 1,3333... |
| …………………………………… 6 | F# | 45/32 = 1,40625 |
| ………… 1 | G | 3/2 = 1,5 |
| …………………… 3 | A | 5/3 = 1,6666... |
| ……………………………… 5 | H | 15/8 = 1,875 |
| …… 0 | C | 2 |
Nu er det syntoniske komma på 81/80 = 1,0125 fjernet fra tertserne i de nævnte akkorder. Til gengæld er den opstået som forskelle i heltonerne. Mellem C og D er intervallet en (stor) sekund på 9/8 = 1,125, og det samme gælder intervallerne mellem F og G og mellem A og H. Men intervallerne mellem D og E og mellem G og A er begge på kun 10/9 = 1,1111..., selvom man også kalder dette interval en stor sekund. Forskellen på de to størrelser sekund bliver (9/8) : (10/9) = 81/80, altså det syntoniske komma.
Tre store tertser oveni hinanden skulle give en oktav, altså en faktor på 2, men (5/4)^3 = 125/64 = 1,953125. Denne forskel på 2 : (125/64) = 128/125 = 1,024 kaldes en diësis, og den får betydning, når man skal afgøre om én af de resterende halvtoner skal stemmes en stor terts oppefra eller nedefra. Den næste tone i kvintcirklen efter F# er C#/Db. Hvis man vælger, at A skal have en ren stor terts, bliver faktoren for C# 25/24 = 1,041666... Hvis man derimod vælger den som et Db som en ren stor terts under F, bliver faktoren for Db 16/15 = 1,0666... Forskellen på de to stemninger for hhv. Db og C#, altså (16/15) : (25/24) bliver netop en diësis på 128/125 = 1,024.
Den første måde at stemme halvtonen C# på med en faktor på 25/24 i forhold til C kaldes en kromatisk halvtone. Dette er også forskellen på en stor terts (dur-terts) og en lille terts (mol-terts). C hhv. C# stemmer jo netop som en lille hhv. stor terts over A. Den anden måde at stemme halvtonen Db med en faktor på 16/15 i forhold til C kaldes en diatonisk halvtone, fordi det faktisk er det samme interval som de to halvtonetrin, der er opstået i ovenstående rene diatoniske skala, nemlig intervallerne mellem E og F og mellem H og C, begge på 16/15 = 1,0667... Den diatoniske halvtone er et "naturligt" interval, fordi det netop er intervallet fra den 15. til den den 16. naturtone, og da den 16. naturtone er den samme som grundtonen forhøjet med 4 oktaver, kan man opfatte dette interval som en naturlig ledetone.
En diêsis er altså det samme som forskellen på en diatonisk halvtone (16/15) og en kromatisk halvtone (25/24).
Ligesvævet stemning
Man kan således ikke stemme fx et klaver ved hjælp af naturtonerne. Her bruger man i stedet en stemning med såkaldt ligesvævende temperatur, hvor alle halvtonetrin er defineret ved faktoren 21/12 ≈ 1,0595, hvilket giver et heltonetrin med faktor 1,1225. I den tempererede stemning får en kvint så faktoren 1,4983 i stedet for den rene stemning 1,5.
Ved ligesvævende temperatur fastholder man frekvensen på kammertonen a1 på 440 Hz og justerer de andre toner i forhold til den.
| Tone | Frekvens |
|---|---|
| c1 | 261,6 |
| cis1 = des1 | 277,2 |
| d1 | 293,7 |
| dis1 = es1 | 311,1 |
| e1 | 329,6 |
| f1 | 349,2 |
| fis1 = ges1 | 370,0 |
| g1 | 392,0 |
| gis1 = as1 | 415,3 |
| a1 | 440,0 |
| ais1 = b1 | 466,2 |
| h1 | 493,9 |
| c2 | 523,3 |
