Funktion (matematik)
 For alternative betydninger, se Funktion. (Se også artikler, som begynder med Funktion)
For alternative betydninger, se Funktion. (Se også artikler, som begynder med Funktion)
En funktion eller afbildning er i matematisk forstand et redskab, der beskriver sammenhængen mellem en såkaldt uafhængig variabel og en anden, såkaldt afhængig variabel. Et hverdagseksempel på en funktion, er sammenhængen mellem hvor meget man bruger sin telefon i løbet af en måned, og hvad man betaler for det: Her er den forbrugte taletid den uafhængige variabel, mens prisen er den afhængige variabel – »afhængig« fordi den afhænger af forbruget. Operator og transformation[1][2] er andre navne anvendt for funktion.
Funktioner er specialtilfælde af det matematiske begreb relation: Det særlige ved en funktion er, at der til en bestemt værdi af den uafhængige variabel hører én og kun én værdi for den afhængige variabel[3] – andre relationer "har lov til" at knytte mere end én værdi for den afhængige variabel, til hver mulig værdi af den uafhængige variabel. Set i forhold til eksemplet med telefonen betyder det, at der kun er knyttet én pris (værdi af den afhængige variabel) til et bestemt forbrug (værdi af den uafhængige variabel); hvis man brugte den samme mængde taletid i løbet af hver måned, ville man få en telefonregning på det samme beløb måned efter måned (her ses bort fra udlands-takster, prisændringer m.v.).
Notation
Kalder man den uafhængige variabel for x og den afhængige variabel for y, skrives en funktion helt kort som
- y = f(x)
Denne notation blev første gang brugt af matematikeren Leonhard Euler. Bogstaverne x og y skal blot betragtes som "pladsholdere" for tal, mens f er et "navn", der gør det muligt at kende flere funktioner fra hinanden; navnet kan være et eller flere bogstaver. Nogle funktioner har "vedtagne" navne (som f.eks. cos for cosinus) I mere generelle situationer, f.eks. opgaver og eksempler i lærebøger, bruges oftest f, g, h osv., på samme måde som generelle eksempler på ligninger traditionelt bruger bogstavet x for den ubekendte størrelse.
Forskrift
Den nøjere sammenhæng mellem den uafhængige og afhængige variabel kan være givet ved det der kaldes funktionens forskrift: Det er regneudtryk, der direkte beregner værdien af den afhængige variabel ud fra en given værdi af den uafhængige. Hvis telefonen i ovenstående eksempel koster 25 kr. om måneden i abonnement, plus 50 øre (½ krone) pr. samtaleminut, kan man opstille en forskrift for en funktion f, der beregner den månedlige telefonregning:
- f(x) = ½·x + 25
Her står x for det antal minutter man har talt i telefon i en given måned: Hvis man erstatter x'et i regneudtrykket til højre for lighedstegnet med antallet af samtaleminutter, får man et ganske almindeligt regnestykke – resultatet af det regnestykke er det beløb der står på telefonregningen for den måned. En funktion kan have flere forskellige forskrifter som giver de samme værdier for funktionen og det er derfor i den sammenhæng bedre at kalde forskrifterne for repræsentationer af funktionen. En repræsentation af en funktion kan fx være en sum af uendelig mange tal, som ofte er det eneste man kan finde. Det er ikke nødvendigvis sådan at summen er et endeligt tal for alle x værdier af interesse, summen kan blive uendelig. Summen skal så omformes til en anden repræsentation, et endeligt udtryk eller en sum der summeres op til et endeligt tal. Dette er meget ofte muligt.
Definitions-, dispositions- og værdimængde
For en given funktion findes der tre mængder med særlig relevans: Definitionsmængden til en funktion f, der ofte skrives som Dm(f), dispositionsmængden, og værdimængden til f, der tilsvarende skrives som Vm(f). Funktionen f siges at være "defineret på mængden Dm(f)".
Definitionsmængde
Definitionsmængden til en funktion er mængden af samtlige de værdier for den uafhængige variabel x, som kan bruges med den pågældende funktion. Eksempelvis giver det i ovenstående eksempel med telefonregningen ikke mening at bruge negative tal for antallet af samtaleminutter x. Af den grund må man forlange, at x ikke er et negativt tal, når man bruger telefonregnings-funktionen f; dette gøres ved at begrænse definitionsmængden til alle reelle tal større end eller lig med nul. I dette tilfælde skyldes begrænsningen, at visse tal ikke giver mening i forhold til den virkelighed, funktionen bruges til at beskrive: Selv om man ikke kan tale i telefon i negativ tid, er der ingen aritmetiske hindringer for at erstatte x med −5 i føromtalte forskrift for funktionen f.
Andre funktioner benytter sig af operationer med begrænsede definitionsmængder, som f.eks.
som er defineret på ℝ\{0}, eller
som ikke er defineret for negative tal, hvis der ses bort fra komplekse tal.
Dispositionsmængde
Dispositionsmængden er den mængde, som funktionen afbilder definitionsmængden ind i, og er dermed altid en overmængde til værdimængden. Givet en funktions forskrift og definitionsmængde, men ikke dens dispositionsmængde, er det ikke nødvendigvis muligt at bestemme denne.
Værdimængde
Værdimængden til en funktion er mængden af samtlige værdier som den afhængige variabel kan antage for den funktion. I eksemplet med telefonregningen betaler man som minimum et vist beløb (det faste abonnement) hver måned for at have telefonen – uanset hvor meget eller lidt man bruger telefonen, kommer regningerne aldrig ned under denne minimumsgrænse. Værdimængden Vm(f) til telefonregningsfunktionen f er dermed alle reelle tal, der er større end eller lig med abonnementsprisen.
Som for definitionsmængden kan der også være aritmetiske årsager til, at visse tal ikke optræder i en funktions værdimængde. I tilfældet med findes der ikke noget tal x, som i den viste forskrift giver resultatet nul – af den grund hører nul ikke til værdimængden for funktionen g.
In-, sur- og bijektivitet

En funktion kaldes injektiv, hvis hvert element i dispositionsmængden bliver afbildet af højst ét element i definitionsmængden, dvs. hvis
f(x) = f(x') ⇒ x = x'
En funktion kaldes surjektiv, hvis der til ethvert y i dispositionsmængden eksisterer mindst ét element x i definitionsmængden, der opfylder f(x) = y. For en surjektiv funktion er dispositionsmængde og værdimængde en og samme ting. En funktion, der er både injektiv og surjektiv, kaldes bijektiv.[4]
Monotoni
Visse funktioner, som eksemplet med f(x) = ½·x + 25, har den egenskab, at uanset hvilken værdi man vælger for den uafhængige variabel x, så vil en lille stigning i x's værdi medføre en stigning i den afhængige størrelse y = f(x): Sådan en funktion siges at være monotont voksende – »monotont« eftersom den afhængige variabel aldrig "laver andet" end at stige, uanset hvilken værdi af den uafhængige variabel x man går ud fra.
Med andre funktioner, f.eks. y = g(x) = 1/x vil y konsekvent falde hvis man forøger x en kende: Sådanne funktioner omtaler matematikerne tilsvarende som monotont aftagende. Atter andre funktioner, som f.eks. sinus og cosinus er voksende indenfor bestemte intervaller for x, og aftagende når x falder imellem disse intervaller.
I forbindelse med funktionsanalyse gør man ofte rede for i hvilke intervaller den analyserede funktion er hhv. voksende og aftagende; denne redegørelse kaldes almindeligvis for funktionens monotoniforhold. Disse monotoniforhold bestemmes ofte ved hjælp af differentialregning, idet den afledede funktions fortegn er positivt, nul og negativt, når den oprindelige funktion er hhv. voksende, konstant og aftagende.
Graf for en funktion
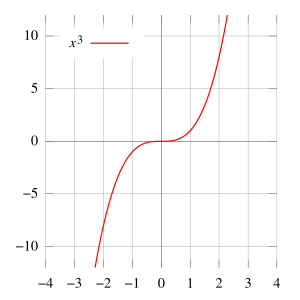
f(x) = x3
Ofte kan man skabe et hurtigt, visuelt overblik over en funktion, ved at tegne en graf (ofte kaldet en kurve) over, hvordan den afhængige variabel udvikler sig hen over et interval.
Til højre er vist et eksempel på en graf, i dette tilfælde over en funktion f(x) = x³ Her kan man med et enkelt blik se hvordan den afhængige variabel generelt stiger ret kraftigt – undtagen i området omkring x=0, hvor "væksten" tilsyneladende tager en kort "pause".
Invers funktion
Hvis en funktion f(x) er bijektiv, findes der en invers eller omvendt funktion til den pågældende funktion, som skrives f-1(x): Denne inverse funktion kan tage imod et tal der er beregnet med f(x), og så at sige "regne baglæns" for at finde tilbage til x; Hvis f(x) = y, så vil f -1(y) være lig med x.
Heraf ses, at definitionsmængden til f, bliver værdimængden til f -1, og vice versa. Altså:
Dm(f) = Vm(f -1), og Vm(f) = Dm(f -1).
Hvis en funktion ikke er injektiv, kan den ikke umiddelbart inverteres, idet nogle elementer i dens værdimængde vil blive afbildet af mere end ét element; en afbildning af en mængde, derimod, har altid en modsat afbildning. Dog kan man ved at begrænse funktionens definitionsmængde gøre funktionen invertibel, som det er tilfældet med sinusfunktionen. Sinusfunktionen er monotont tiltagende i [-π/2, π/2], som den afbilder i [-1, 1]; derfor kan den her inverteres, hvorved arcsin-funktionen er defineret. sin-1 er en udbredt måde på hvilken at udtrykke det samme.
Regning med funktioner
Når f og g er funktioner med samme (eller i det mindste overlappende) definitionsmængder kan man indføre nye funktioner f+g, f-g, f·g og f/g ved punktvise operationer. Det vil sige at de nye funktioner er defineret ved
- (f+g)(x) = f(x) + g(x)
- (f−g)(x) = f(x) − g(x)
- (f·g)(x) = f(x)·g(x)
- (f/g)(x) = f(x)/g(x)
Bemærk at den sidste funktion ikke er defineret for x sådan at g(x)=0, også selvom både f og g er; et forhold mellem funktioner er ikke nødvendigvis defineret alle de steder de funktioner den består af er.
Særlig agtpågivenhed må udvises når skrivemåder som f3 anvendes, altså potenser af en funktion. Notationen kan nemlig fortolkes på to måder: enten som punktvis multiplikation (som ovenfor) eller som funktionssammensætning. Eksplicit kan f3 betyde
eller
Hvilken betydning der bruges må forstås af sammenhængen.
Særlige funktioner
I det følgende nævnes en række funktioner og kategorier af funktioner, som behandles i særskilte artikler:
- Trigonometriske funktioner, herunder sinus, cosinus og tangens.
- Logaritmer
- Polynomier
- Potensfunktioner
- Eksponentialfunktioner
Se også
Bog
- Holth, Klaus m.fl. (1987): Matematik Grundbog 1. Forlaget Trip, Vejle. ISBN 87-88049-18-3
Kildehenvisninger
- ^ Fra en:Transformation (function) Citat: "...In other areas of mathematics, a transformation may simply be any function, regardless of domain and codomain...."
- ^ P. R. Halmos (1960). Naive Set Theory. Springer Science & Business Media. s. 30–. ISBN 978-0-387-90092-6. Arkiveret fra originalen 21. juli 2020. Hentet 21. september 2019.
- ^ Holth (1987) s. 71
- ^ Peter Bollerslev: Matematik i læreruddannelsen: Kultur, Kundskab og Kompetence 2, ss. 69-71. Nordisk Forlag A.S. Copenhagen, 1998
 |
Wikimedia Commons har medier relateret til: |




