ZFK equation
ZFK equation, abbreviation for Zeldovich–Frank-Kamenetskii equation, is a reaction–diffusion equation that models premixed flame propagation. The equation is named after Yakov Zeldovich and David A. Frank-Kamenetskii who derived the equation in 1938 and is also known as the Nagumo equation.[1][2] The equation is analogous to KPP equation except that is contains an exponential behaviour for the reaction term and it differs fundamentally from KPP equation with regards to the propagation velocity of the traveling wave. In non-dimensional form, the equation reads
with a typical form for given by
where is the non-dimensional dependent variable (typically temperature) and is the Zeldovich number. In the ZFK regime, . The equation reduces to Fisher's equation for and thus corresponds to KPP regime. The minimum propagation velocity (which is usually the long time asymptotic speed) of a traveling wave in the ZFK regime is given by
whereas in the KPP regime, it is given by
Traveling wave solution
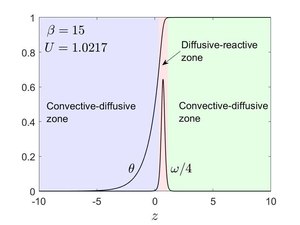
Similar to Fisher's equation, a traveling wave solution can be found for this problem. Suppose the wave to be traveling from right to left with a constant velocity , then in the coordinate attached to the wave, i.e., , the problem becomes steady. The ZFK equation reduces to
satisfying the boundary conditions and . The boundary conditions are satisfied sufficiently smoothly so that the derivative also vanishes as . Since the equation is translationally invariant in the direction, an additional condition, say for example , can be used to fix the location of the wave. The speed of the wave is obtained as part of the solution, thus constituting a nonlinear eigenvalue problem.[3] Numerical solution of the above equation, , the eigenvalue and the corresponding reaction term are shown in the figure, calculated for .
Asymptotic solution[4]
The ZFK regime as is formally analyzed using activation energy asymptotics. Since is large, the term will make the reaction term practically zero, however that term will be non-negligible if . The reaction term will also vanish when and . Therefore, it is clear that is negligible everywhere except in a thin layer close to the right boundary . Thus the problem is split into three regions, an inner diffusive-reactive region flanked on either side by two outer convective-diffusive regions.
Outer region
The problem for outer region is given by
The solution satisfying the condition is . This solution is also made to satisfy (an arbitrary choice) to fix the wave location somewhere in the domain because the problem is translationally invariant in the direction. As , the outer solution behaves like which in turn implies
The solution satisfying the condition is . As , the outer solution behaves like and thus .
We can see that although is continuous at , has a jump at . The transition between the derivatives is described by the inner region.
Inner region
In the inner region where , reaction term is no longer negligible. To investigate the inner layer structure, one introduces a stretched coordinate encompassing the point because that is where is approaching unity according to the outer solution and a stretched dependent variable according to Substituting these variables into the governing equation and collecting only the leading order terms, we obtain
The boundary condition as comes from the local behaviour of the outer solution obtained earlier, which when we write in terms of the inner zone coordinate becomes and . Similarly, as . we find . The first integral of the above equation after imposing these boundary conditions becomes
which implies . It is clear from the first integral, the wave speed square is proportional to integrated (with respect to ) value of (of course, in the large limit, only the inner zone contributes to this integral). The first integral after substituting is given by
KPP–ZFK transition

In the KPP regime, For the reaction term used here, the KPP speed that is applicable for is given by[5]
whereas in the ZFK regime, as we have seen above . Numerical integration of the equation for various values of showed that there exists a critical value such that only for , For , is greater than . As , approaches thereby approaching the ZFK regime. The region between the KPP regime and the ZFK regime is called the KPP–ZFK transition zone.
The critical value depends on the reaction model, for example we obtain
Clavin–Liñán model
To predict the KPP–ZFK transition analytically, Paul Clavin and Amable Liñán proposed a simple piecewise linear model[6]
where and are constants. The KPP velocity of the model is , whereas the ZFK velocity is obtained as in the double limit and that mimics a sharp increase in the reaction near .
For this model there exists a critical value such that
See also
References
- ^ Zeldovich, Y. B., & Frank-Kamenetskii, D. A. (1938). The theory of thermal propagation of flames. Zh. Fiz. Khim, 12, 100-105.
- ^ Biktashev, V.N.; Idris, I. (2008). "Initiation of excitation waves: An analytical approach". 2008 Computers in Cardiology. pp. 311–314. doi:10.1109/CIC.2008.4749040. ISBN 978-1-4244-3706-1. S2CID 15607806.
- ^ Evans, L. C. (2010). Partial differential equations (Vol. 19). American Mathematical Soc.
- ^ Williams, F. A. (2018). Combustion theory. CRC Press.
- ^ Clavin, P., & Searby, G. (2016). Combustion waves and fronts in flows: flames, shocks, detonations, ablation fronts and explosion of stars. Cambridge University Press.
- ^ Clavin, P., & Liñán, A. (1984). Theory of gaseous combustion. In Nonequilibrium Cooperative Phenomena in Physics and Related Fields (pp. 291-338). Springer, Boston, MA.




![{\displaystyle \theta \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fead1e7dceab4be5ab2e91f5108144722daa8c36)





























































