User:Homunq/If after all there is a vote
Wikipedia is not about voting. Consensus is preferred, whenever possible.
However, there are still some cases in which voting is the only answer. When two or more sides each have a strong interest and a reasonable argument from policy, at some point the slow-motion (hopefully) edit war has to stop. That's what happened with the Ireland article; and it will surely happen again some day.
In this case, the voting system (or at least, !voting system) used is important. It is well-known that, depending on the voting method, there is always some possibility that voting strategy could change the result. Furthermore, many voting systems have obvious strategy problems. For instance, Felsenthal and Machover [1] found, using real-world election data, that plurality voting, the most commonly-used voting system, was also the most likely to elect the candidate who would have lost a runoff.
Desirable characteristics
The election system used by wikipedia should have the following general characteristics (many of which are associated with one or more formal voting criteria in this table):
- It should be easy, even "foolproof", for !voters; and compatible with existing !voting behavior on wikipedia
- That is, it should be easy to interpret a comment like "I strongly favor options B and D. I don't like E, and I hate A and G" as a valid ballot.
- There should be no arbitrary restrictions on the form of the ballot (say, to be a full preference ordering of the options).
- (This generally corresponds to the colums ">2 ranks" and "= ranks" in the table. If skipped ranks must also be allowed, it corresponds to "scores" in the "ballot type" column)
- It should not encourage any obvious strategy by which a partisan minority could easily try to sway the result
- In as many cases as possible, naive !voters should have as much power as sophisticated, strategic ones.
- It should be monotonic, so there is never a case where one more !vote for the current winning option could cause it to lose. (Such a situation could cause crazy strategies and/or recriminations.)
- (This generally corresponds to the colums "Later-no-harm/Later-no-help" and "FBC:No favorite betrayal" in the table. The "monotone" and "cloneproof" columns are also desirable)
- As much as possible, it should encourage, or at least allow for, compromise and consensus
- (Insofar as this shows up in the table, it is in the "MMC" column)
- It should be as easy to count as possible for volunteer administrators, and give a clear answer.
- (Insofar as this shows up in the table, it is in the "Summable" and "Polytime/Resolvable" columns)
- The results should be as comprehensible as possible for editors unversed in the details of voting theory
- (This is not covered in the criteria table)
- The system should be well-understood by voting theorists, so that its coherence with the above criteria is agreed-on by all.
- (This is true of all systems in the criteria table. Systems not in the table may or may not meet this criterion.)
Process characteristics independent of voting system
A wikipedia !vote should tend to discourage sockpuppets and meatpuppets, and to take account of strength of arguments and not just sheer numbers. However, it is impossible for any voting system to inherently accomplish this; this is dependent on the judgment of the closing administrator(s). The term "!vote" (read as "not-vote") is used in this essay to remind readers of this fact.
Solution
There is no single !voting system which meets all of these desiderata. However, by combining two closely-related systems, you can (almost always) satisfy them all. Majority Judgment (MJ) meets criteria 1-4 and 6; and Graduated Majority Judgment (GMJ), a small adjustment which gives the same result in all but exceptional circumstances, meets criteria 1-5. So if the actual system used is MJ, but the results are reported based on GMJ, then all 6 criteria will be met — except in the rare cases where these two systems disagree.
After explaining how and why this would work, this essay will consider other voting system options, and show why none meet these criteria nearly as well.
Please note that this is not a one-size-fits-all solution. While Majority Judgment is a good system overall, there are situations where I'd recommend others even more highly. For US president, I'd recommend Approval; for US Senate, SODA Voting; for most congressional and parliamentary systems, a biproportional system such as PAL voting; in Robert's Rules situations, approval with runoffs; and in loose internet voting, Score Voting. Such flexibility is the spirit of the Declaration of Election Method Reform Advocates.[2][3]
If options are on a scale
If there is a poll between options like no pie, a small slice of pie, a whole pie, and nothing but pie, these should be considered as an ordinal scale. In this case, in order to find consensus, it helps to look at the median option. If that option has a significant number of !votes in its own right, then that-much-or-more will have a majority against less-than-that, while that-much-or-less also has a majority against more-than-that.
(This subsection, unlike the rest of this essay, is only given as guidance in finding consensus, as it is unlikely that a disagreement of this sort would fail to be resolved eventually by normal discussion processes.)
Mechanics
!Voters would be instructed as follows:
(A shorthand format for votes would be easy to work out and include in the instructions.)
Any !voters who didn't explicitly assign the options to categories would have their votes interpreted as if they had (unless they specifically ask not). Interpretations will attempt to preserve any distinctions and groupings that the voter made, and to assign at least one option each the two "strongly" categories. Any options not mentioned in a !vote would be counted as the non-strong option as far from the explicitly-given options as possible (so a vote that only mentions "support" will have unmentioned items classed as "oppose")
Each type of !vote for each option will be tallied. Say that option A has (1,2,4,3,5) !votes (ordered from opposition to support), and option B has (2,1,2,6,4). These tallies are enough to find the medians for each option - in this case, "support" for both. If one option has the highest median, that option !wins.
To calculate the Majority Judgment tiebreaker, drop 1 median !vote at a time from all tied candidates at once until they differ. In the example, after dropping 1 "support" from A and B, they have (1,2,4,2,5) and (2,1,2,5,4) respectively, leaving A with a rounded-down median of "neutral" and B still with "support". B !wins.
To calculate the Continuous Majority Judgment score, you use the formula:
- Median + ((Votes_above_median - Votes_below_median) / (2 * Votes_at_median))
(Median is a number between 0 and 4)
A's CMJ score is 3+((5-7)/(2*3)) or 2.67. B's is 3+((4-5)/(2*6)) or 2.92. As with MJ, B !wins.
So the verdict in this case would be that B wins, because of MJ. The CMJ scores would be posted, to give an easily-understandable measure of how much B had !won by. It would also be reasonable to multiply by 25 in order to map the 0—4 range of the CMJ scores onto a 0—100 range, and say that in this case A got 66.7 and B got 72.9.
Full Example
Say the options are 1-5, and the following !votes are cast:
- Support 2 and 4, because roses are red. Romantic (talk) 12:42, 19 September 2012 (UTC)
- Oppose 2, because the sky is blue. Realist (talk) 13:37, 19 September 2012 (UTC)
- Strongly support 1; grass is green. Support 3; fifty shades of grey. Strongly oppose 5; oranges are not the only fruit. Novelist (talk) 14:07, 19 September 2012 (UTC)
- Strongly support 4; violets are blue. Support 1, per Novelist. Neutral on 2. Oppose 3; grey poupon. Strongly oppose 5, again per Novelist. Me22 (talk) 16:47, 19 September 2012 (UTC)
- Strongly support 5; support 3. Laconic (talk) 17:40, 19 September 2012 (UTC)
These !votes would be interpreted as: (using SO, O, N, S, SS for grades, and giving the grades of the 5 options in order)
- O, SS, O, SS, O
- S, SO, S, S, S
- SS, N, S, N, SO
- S, N, O, SS, SO
- O, O, S, O, SS
So the tallies and CMJ scores for each option would be:
- O1: (0, 2, 0, 2, 1) CMJ 2.75
- O2: (1, 1, 1, 0, 2) CMJ 2
- O3: (0, 2, 0, 3, 0) CMJ 2.67
- O4: (0, 1, 1, 1, 2) CMJ 3
- O5: (2, 1, 0, 2, 0) CMJ 1
Option 4 is the winner with both MJ and CMJ.
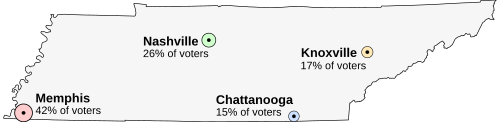
Standard example
Suppose that Tennessee is holding an election on the location of its capital. The population is concentrated around four major cities. All voters want the capital to be as close to them as possible. The options are:
- Memphis, the largest city, but far from the others (42% of voters)
- Nashville, near the center of the state (26% of voters)
- Chattanooga, somewhat east (15% of voters)
- Knoxville, far to the northeast (17% of voters)
The preferences of each region's voters are:
| 42% of voters Far-West |
26% of voters Center |
15% of voters Center-East |
17% of voters Far-East |
|---|---|---|---|
|
|
|
|
Suppose voters assigned their ratings to the four cities by giving their own city the rating "Strongly support", the farthest city the rating "Strongly oppose" and the other cities "Support", "Neutral", or "Oppose" depending on whether they are less than a hundred, less than two hundred, or over two hundred miles away:
City Choice |
Memphis voters |
Nashville voters |
Chattanooga voters |
Knoxville voters |
Median rating[4] |
|---|---|---|---|---|---|
| Memphis | SS | SO | SO | SO | SO+ |
| Nashville | N | SS | N | N | N+ |
| Chattanooga | O | N | SS | S | N- |
| Knoxville | SO | N | S | SS | N- |
Then the sorted scores would be as follows:
| City |
|
||||||||||||
| Memphis |
|
||||||||||||
| Nashville |
|
||||||||||||
| Chattanooga |
|
||||||||||||
| Knoxville |
|
||||||||||||
|
The median ratings for Nashville, Chattanooga, and Knoxville are all "Fair"; and for Memphis, "Poor". Since there is a tie between Nashville, Chattanooga, and Knoxville, Majority Judgment breaks this tie by removing "Fair" ratings from all three, until their medians become different. This is essentially the same as looking for each candidate's rating transition closest to the middle, and breaking median ties by choosing the candidate where that's furthest to the right.
| City |
|
||||||||||||||||||||
| Memphis |
|
||||||||||||||||||||
| Nashville |
|
||||||||||||||||||||
| Chattanooga |
|
||||||||||||||||||||
| Knoxville |
|
||||||||||||||||||||
|
The CMJ tiebreaker effectively looks a little further out than that. Instead of focusing on the closest transition to the center, it effectively takes a weighted average of a balanced central region which includes all of the median votes (that is, extending out as far as the second-closest transition to the center). To take this average, all votes in this region are treated as if they were within one category of the median.
In the table below, votes changed by this assumption are shown in their actually-cast versions as well as the virtual within-1-step-of-the-median versions used for the average. Three of the four cities have such "virtual" votes, because their ratings jump discontinuously over some rating that no voters gave them. That's an effect of this artificial example, where all the voters live in the cities. In a more realistic example, where voters varied more in where they lived and/or their threshold between levels of support, the necessity for "virtual votes" would be far less common.
| City |
|
||||||||||||||||||||
| Memphis |
|
||||||||||||||||||||
| Nashville |
|
||||||||||||||||||||
| Chattanooga |
|
||||||||||||||||||||
| Knoxville |
|
Option
After tallying the !votes, but before finding the !result, a number of "strongly negative" !votes could be added to all the options. This has the effect of moving the median point to a supermajority requirement; and thus encouraging consensus and compromise (desirable characteristic #3 above). For instance, if 20% of the real !votes were added as "strongly negative" virtual !votes, the effective median point would be moved from 50% to 60% (since 40+20=60). That is, each option would be given the grade that 60% of the !voters could agree it at least deserved.
I believe using a number around 20% would give a better, "more wikepedian" result. If there were two roughly equal factions, they would both be forced to seek a compromise, instead of everyone knowing that whichever faction was larger would be able to steamroll the other. The disadvantage of this option is that it adds a "free parameter" which could be argued about in and of itself. Therefore, if this option is used, I think it should be decided by some arbitrary authority/ benevolent dictator (ie, ArbCom). If I were such a dictator, I'd use 20%; but if there is no such dictator to be had, I wouldn't use this option.
If this option were used at 20% with the example above, the tallies and CMJ scores for each option would be:
- O1: (1, 2, 0, 2, 1) CMJ 2
- O2: (2, 1, 1, 0, 2) CMJ 1.5
- O3: (1, 2, 0, 3, 0) CMJ 2
- O4: (1, 1, 1, 1, 2) CMJ 2.5
- O5: (3, 1, 0, 2, 0) CMJ 0.5
Option 4 is still the winner with both MJ and CMJ.
Compliance
How does this system do on the desirable criteria listed above?
- Easy for voters
- Majority judgment, a "scored" system which uses verbal grades by preference, passes with flying colors, as the example above shows.
- It should not encourage any obvious strategy by which a partisan minority could easily try to sway the result
- No voter or minority subset of voters who agree on the rating an option deserves can do anything strategically to bring the median closer to that rating.
- Specifically, it would NOT help a minority of voters to either exaggerate a vote (by adding "strong"), or to vote a less-preferred option above a more-preferred one.
- (Strategy is still a possibility, but it can only work by making an option get a median higher or lower than you think it deserves, in order to beat/lose to an option whose median you think is even further out of line. Thus, in general, the only people able to use strategy - those who rated the winner above the winning median, or a loser below the winning median - are the ones with the weakest motives to do so.)
- It is monotonic and cloneproof.
- As much as possible, it should encourage, or at least allow for, compromise and consensus
- By allowing "all options good" and "neutral" votes, this system does pretty well. With the optional supermajority threshold, it does even better.
- It should be as easy to count as possible for volunteer administrators, and give a clear answer.
- This system is polytime, resolvable, and summable at O(N).
- The results should be as comprehensible as possible for editors unversed in the details of voting theory
- GMJ assigns a single number to each option, and the highest number wins. That's pretty easy to follow. There could be rare cases when the MJ winner did not agree with the GMJ winner, but even then, GMJ would show that the MJ winner had been close.
- The system should be well-understood by voting theorists, so that its coherence with the above criteria is agreed-on by all.
- This is true of MJ, but there has been little study of GMJ.
Inferior alternatives for this use case
This badly fails almost all the desirable criteria except #5.
Instant runoff voting / Alternative Vote / Hare
This badly fails 1, 2, and 4, and doesn't do as well as MJ on 3.
These don't do as well as MJ on 2, and clearly fail 4 and 5.
This does well on 4, 5, and 6, but is barely acceptable on 1, 2, and 3.
Range voting / Score voting
Score voting and MJ are actually quite similar on the whole; as similar as the mean and the median. Thus, even though there is not a huge difference on the desirable characteristics, what difference there is is directly comparable. This allows us to see that MJ is detectably better on 1 and 3, and considerably better on 2.
Specifically, in Score voting, strategic exaggeration is always a viable strategy for any voter whose honest vote isn't already fully exaggerated; in MJ, it almost never is.
This is the system (with some modifications) that was used in the initial round of the abortion article naming debate, and it was a total failure. As the person who did the count, I can personally attest that without a doubt it badly failed 1 and 4, and in my opinion it also badly failed 2 and 3.
This is unacceptable, as it completely fails criterion 4 by not giving a usable answer after a single round of voting. It's hard enough for the admins to handle one round; stretching the process to two rounds of voting is unacceptable.
Though this can be an excellent voting system in some cases, for Wikipedia it would simply be a bureaucratic nightmare which overtly encourages vote-stuffing.
References
- ^ Felsenthal, D. S., and M. Machover. “Who Ought to Be Elected and Who Is Actually Elected? An Empirical Investigation of 92 Elections Under Three Procedures.” Electoral Studies 14, no. 2 (1995): 143–169.
- ^ Quinn, Jameson. "Declaration of Election-Method Reform Advocates". Retrieved April 22 2012.
{{cite web}}: Check date values in:|accessdate=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Tawfik, Adrian (April 22, 2012). "Democracy Chronicles Interviews Election Experts". Democracy Chronicles. Retrieved April 22 2012.
{{cite web}}: Check date values in:|accessdate=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ A "+" or "-" is added depending on whether the median would rise or fall if median ratings were removed, as in the tiebreaking procedure.