Wedge (geometry)
| Wedge | |
|---|---|
 | |
| Faces | 2 triangles, 3 quadrilaterals |
| Edges | 9 |
| Vertices | 6 |
In solid geometry, a wedge is a polyhedron defined by two triangles and three trapezoid faces. A wedge has five faces, nine edges, and six vertices.
Properties
A wedge is a polyhedron of a rectangular base, with the faces are two isosceles triangles and two trapezoids that meet at the top of an edge.[1]. A prismatoid is defined as a polyhedron where its vertices lie on two parallel planes, with its lateral faces are triangles, trapezoids, and parallelograms;[2] the wedge is an example of prismatoid because of its top edge is parallel to the rectangular base.[3] The volume of a wedge is where the base rectangle is by , is the apex edge length parallel to , and is the height from the base rectangle to the apex edge.[1]
Examples
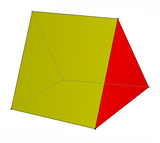
In some special cases, the wedge is the right prism if all edges connecting triangles are equal in length, and the triangular faces are perpendicular to the rectangular base.[3]
Wedges can be created from decomposition of other polyhedra. For instance, the dodecahedron can be divided into a central cube with 6 wedges covering the cube faces. The orientations of the wedges are such that the triangle and trapezoid faces can connect and form a regular pentagon.
Two obtuse wedges can be formed by bisecting a regular tetrahedron on a plane parallel to two opposite edges.
 Obtuse wedge as a bisected regular tetrahedron |
 A wedge constructed from 8 triangular faces and 2 squares. It can be seen as a tetrahedron augmented by two square pyramids. |
 The regular dodecahedron can be decomposed into a central cube and 6 wedges over the 6 square faces. |
References
- ^ a b Harris, J. W.; Stocker, H. (1998). ""Wedge". §4.5.2". Handbook of Mathematics and Computational Science. New York: Springer. p. 102. ISBN 978-0-387-94746-4.
- ^ Alsina, Claudi; Nelsen, Roger B. (2015), A Mathematical Space Odyssey: Solid Geometry in the 21st Century, Mathematical Association of America, p. 85, ISBN 978-0-88385-358-0.
- ^ a b Haul, Wm. S. (1893). Mensuration. Ginn & Company. p. 45.





