User talk:Wcherowi/Archive 4
| Archive 1 | Archive 2 | Archive 3 | Archive 4 | Archive 5 | Archive 6 |
Is multiplication recursive addition?
Howdy. You recently removed my claim from this article that the multiplication sign "symbolizes repeated (i.e., recursive) addition", calling it "ambiguous and technically not correct". I hope this question isn't too bothersome, but would you mind explaining to me how that statement is ambiguous or incorrect? For what it's worth, the source I cited (written by Barbara Oakley, a professor of engineering) states that "the multiplication sign symbolizes repeated addition." While she doesn't use the term recursive, isn't that the same thing? If it isn't, I'm happy to be corrected. I'm not a mathematician so I run the risk of inadvertently misusing math jargon. Thanks. Lord Bolingbroke (talk) 05:52, 21 October 2017 (UTC)
- Here's the longer version of why I removed the sentence. The ambiguity comes from the fact that there are many symbols used in mathematics to indicate multiplication: ×, ⋅, ⊗, nothing (juxtaposition), come to mind immediately and there are other more esoteric symbols used. The sentence read as if there were only one, and, depending on the background of the reader, this could lead to confusion. That, however, is a minor point and the more serious problem is stating that multiplication is repeated addition. This is only true in a very limited setting. Consider trying to explain the product 1/2 × 3/4 as a repeated addition! We actually have an article on this topic (Multiplication and repeated addition). To make the sentence correct would require far more technical verbiage than an article at this level could support. Since the sentence didn't seem to be supporting any point being made, I felt that removing it made more sense than trying to fix it. I hope this helps. --Bill Cherowitzo (talk) 16:28, 21 October 2017 (UTC)
- That makes sense. Thanks for taking the time to explain the rationale behind your edit. The reason I wanted to include that sentence was to illustrate the idea of mathematical symbols being more highly encrypted than regular words. Is there a better example you can think of to make that idea more tangible? Lord Bolingbroke (talk) 05:27, 22 October 2017 (UTC)
- That seems like a good idea. Although examples abound, I am having a hard time coming up with one that is both convincing and at the right level for this article. A good example, although one that I'm afraid might be too advanced for the article, is the prime (') used as a differential operator for single variable functions (as in, f', the derivative of the function f). This simple stroke stands for the limit of a complicated looking quotient involving the function and its variable–quite a lot of packing for the money. --Bill Cherowitzo (talk) 16:51, 22 October 2017 (UTC)
- Yeah, that might be a little too complex to describe succinctly. As I'm not coming up with any better examples, I'll plan on leaving the article in its current state for now. But if a good example comes to mind please do add it into the article. I'll plan on doing the same. Cheers, Lord Bolingbroke (talk) 01:15, 23 October 2017 (UTC)
Descartes
Well, I really don't give a damn. So now you have it and it may stay as you like it. FYI: The original edit was by a learned, highly regarded User, who is also a translator, and obviously a native speaker of French. As I said: go on, flush it all down the drain! - The language and content of the articel is absolutely awful, lots of things are still missing, and the lack of knowledge for many parts is plain to see for all (as eg. the blunder of confounding cognoscere and cogitare etc.) But I don't care to improve that anymore. As I already guessed before: language skills equals "original research", what a shame! That's all. Bye! --89.15.239.196 (talk) 22:41, 12 November 2017 (UTC)
- I am sorry that you feel that way. My request for a citation was meant to clear up the issue, not challenge the translation. As I do not have access to the Routledge Encyclopedia of Philosophy I could not ascertain if they discussed the translation or merely used it. While this translation may be perfectly correct, Wikipedia does not operate on the say-so of its editors, no matter how qualified they may be. It is imperative that the entries be based on published sources so that editors are not in the position of judging the contributions of other editors. Also, the art of translation depends on more than just language skills and the ability to read a source. Historical context plays a major role in getting the translation right, and this requires a specialist. For instance, your concern about confounding cognoscere and cogitare – is this a problem with the translation from Latin to English or is it a problem with the translation from French to Latin? Descartes didn't write this work in Latin and urged others to do the translation for him. You can't deal with this issue without knowing the appropriate context.--Bill Cherowitzo (talk) 23:18, 12 November 2017 (UTC)
- I just added that ref. and it is accessible online. (I don't think, that there are any copyright problems, since they also mention how to quote their article. And it is an official Routledge Website.) Your kind reply gives me some conscience about my rant in the edit note, but sry it's technically impossible to delete it. - Greetings --89.15.239.196 (talk) 00:00, 13 November 2017 (UTC)
The Getting to Philosophy "game"
FYI: I suspect that this edit somehow has something to do with the WP:Getting to Philosophy "game". See for example the edit history at Quantity. Paul August ☎ 16:08, 7 November 2017 (UTC)
- Thanks for bringing that to my attention. I was wondering why someone would choose to mangle the language in that way. --Bill Cherowitzo (talk) 17:48, 7 November 2017 (UTC)
I've been looking into this a bit more and I'm uncovering many more edits related to this "game". You may remember these edits which you reverted. These, just like the one to Element (mathematics) mentioned above, which you also reverted, were intended to break the loop: Mathematics -> Quantity -> Counting -> Element (mathematics) -> Mathematics, and insure that articles, which link to these articles will instead "get to Philosophy". Looking at User Sjtumlin16 edit history, you can see other edits intended to break other such loops, like the Sand fence -> Snow fence -> Sand fence loop, and the Household -> Dwelling -> Household loop. Paul August ☎ 22:03, 15 November 2017 (UTC)
- So the question now is what can we do to discourage this game, other than reverting it when we see it? --Bill Cherowitzo (talk) 22:36, 15 November 2017 (UTC)
I don't have a good answer to that. Paul August ☎ 23:35, 15 November 2017 (UTC)
- Do you think there might be some value in bringing this up on the Wikiproject page? --Bill Cherowitzo (talk) 18:04, 16 November 2017 (UTC)
I suppose it couldn't hurt. Paul August ☎ 18:44, 16 November 2017 (UTC)
Multiplying by 100 to get percents
Regarding my changes you reverted on Relative change and difference: https://en.wikipedia.org/w/index.php?title=Relative_change_and_difference&diff=prev&oldid=744507896
You wrote "To obtain a percentage you multiply by 100 not 100%, check any reliable source; discuss this on the talk page if you must.". I must :). Your comment is incorrect. Just like Percentage states in it's introduction and "Examples" section, the expression "45%" is equal to "0.45", and therefore not equal to "0.45 x 100". An easy way to get around this problem is to multiply by "100%" instead of "100". This is what I edited. This workaround is mathematically correct and is still useful for beginners.
The page currently states that "By multiplying these ratios by 100 they can be expressed as percentages". This is incorrect. Un-multiplied ratios can be expressed perfectly fine as percentages. Most examples on Relative change and difference get this right and do not contain the incorrect "x 100".
These perhaps reliable sources (?) claim that the percent sign stands for "1/100", which is consistent with my viewpoint and inconsistent with yours:
--212.35.11.31 (talk) 23:53, 12 November 2017 (UTC)
- I really do not know what you are talking about.
- So multiplying by 100% is multiplying by 1 and doesn't change anything. To take any number x and write it as a percentage you must first convert it to hundredths, that is, x = 100x/100 and the percentage is the number of hundredths, i.e., 100x. So to convert a number to a percentage, you multiply by 100 and then attach the % sign to indicate the fact that you are expressing the number in terms of hundredths. Your so-called work around is not mathematically correct and blurs what is really going on. This is not something that you should do to beginners since they would have to "unlearn" this as their mathematical ability matures. Also, those sources do not say that the percentage sign stands for 1/100, they say that percent stands for parts per hundred. The symbol has no numerical value. --Bill Cherowitzo (talk) 03:30, 13 November 2017 (UTC)
- The important part is "you multiply by 100 AND THEN ATTACH THE % SIGN". Attaching the % sign is achieved by multiplying by "100%". Only mentioning the multiplication by 100, without attaching a "%" is incorrect. You convert a number to hundredths, not by multiplying by 100, but by extending the fraction: Multiply the nominator AND denominator by 100. If we can agree that 1% = 0.01, it follows that it is wrong to write 1% = 0.01 x 100, yet this is what the page does.
- Could you elaborate why you think my work around is mathematically incorrect?--212.35.11.31 (talk) 10:06, 13 November 2017 (UTC)
- You attach a % sign by attaching the % sign. It is not a number, it is a symbolic abbreviation of a word = percent. The number 0.5 is 50 percent. Are you now telling me that I obtain this by multiplying 0.5 by 100 percent. I know how to multiply numbers, but 0.5 of a word is a bit perplexing (is it perc? or perhaps cent?) If the percent sign had a numerical value, then we would be perfectly happy writing things like (5%)(10%) = 50(%)2!!! Returning to your statement above that attaching the % sign is achieved by multiplying by 100%. If true, then the rule for converting a number to a percentage is to multiply the number by 100 and then multiply by 100% – awkward but at least mathematically sound, but I doubt that anyone would wish to explain this formulation to beginners. --Bill Cherowitzo (talk) 17:39, 13 November 2017 (UTC)
- As I have been thinking about this a little more, I have realized that this is a bit subtler than I first imagined and what I have said above would probably not convince you. So let me take another tack. Yes, 1% = 0.01, no argument there. However, you want to conclude from that that % = 1% = 0.01 or, in the vernacular, % operationally means divide by 100. If "%" were a number I would agree with that, but 1 is the multiplicative identity only in the realm of numbers and if "%" is not a number then this would not make any sense. Consider the following from an operational point of view. Using your concept, 15 × 100% = 1500% = 15 since % means divide by 100. Mathematically correct, but not very useful. What you really want to do is stop at 1500%. In terms of operations, you first multiply 15 by 100 and then adjoin a % sign. The % sign thus gets the operational interpretation of "you ought to divide by 100, BUT YOU DON'T". In other words, it means just the opposite of what it would mean if it were a number.--Bill Cherowitzo (talk) 23:00, 13 November 2017 (UTC)
Just my 2 cents: This problem stems from the very unlucky, but wide spread use of the terms unitless and dimensionless, which are, additionally, used mostly in a sort of synonymous way. Both should be replaced (who am I to demand this!) by unit and dimension of unity. Maybe the abstract notion of numbers in pure math deserves the "xxx-less". However, as soon as there is something real under consideration, some dimension gets involved, e.g., length, quantity (of entities), rank (in a list), ratio (of measures), ... To make things still more complicated, the resulting quantities of these considerations are expressed by an absolute measure (a pure number) times some arbitrary(!) unit, e.g., for length in meter or inch, for quantitiy in dozens(dz) or gross(gr) or in unit unity, the denotation of which by e.g. is generally considered nonessential. Another unit, fitting to the dimension unity, is the , the denotation of a specific unit defined by , analogous to The task under discussion is the adaption of the absolute measure to various units, so that the same quantity is addressed.
I beg pardon, if I missed the generic terms of the English language. For some more examples of units fitting the dimension of unity, please see the German WPZählmaße. Purgy (talk) 09:01, 14 November 2017 (UTC)
- Thanks Purgy, this whole dimension unity thing strikes me as a kludge for the sake of uniformity without much substance. Having grown up with dimensionless, unitless and pure numbers I find it hard to accept these new platitudes. I don't think that this changes the essentials of my argument above.--Bill Cherowitzo (talk) 17:29, 14 November 2017 (UTC)
Bill, I think I understand your viewpoint (and still don't agree) - but I don't think that it's important to agree. My point is this: If , this implies . Only one of the two expressions can be correct. In Relative change and difference#Percentage_change the first formula does not include , the second formula does. Can we agree that the notation on the page is inconsistent? Additionally, if we assume that "%" means "percent", which is a word, not to be used in calculations, then the subtraction and division of percentages in "Example of percentages of percentages" does not make sense. --212.35.11.31 (talk) 19:06, 14 November 2017 (UTC)
- As I mentioned above, this can be a bit subtle. First of all, to clear the air, I never made the claim that 1% = 0.01 × 100, that was something that the IP said I was saying. 0.01 × 100 = 1 = 100% is the only true statement. Here is the subtle part, 1% = 0.01 = ( 0.01 × 100 ) % = (0.01 × 100) percent = (0.01 × 100) pc or any other way you have of indicating that you are talking about the number of hundredths. The % sign is acting as the name of a unit in the sense that you have described above. As to the examples in Relative change and difference, they are both correct-ish and follow the usual conventions. In the first, using numbers, the quantity is calculated as a number and then converted to a percentage (the details of which are not given). In the second formula, the generic calculation is given, but this time the formula is labelled as the percentage change meaning that the result needs to be a percentage which is why the multiplication by 100 is present and no percentage sign is needed because that would be redundant. What would be incorrect here is to write × 100% because that means you are multiplying by 1. Of the two examples it is actually the first one that isn't quite right since it is calculating a percentage change without writing it as a percent (that part being done as a second step). Since percentage is just a way to represent a number I see nothing wrong in subtracting or dividing percentages since it is the numbers that these algebraic manipulations are being applied to.--Bill Cherowitzo (talk) 20:15, 14 November 2017 (UTC)
- Just adding one other platitude:
- In the future I'll try to avoid mentioning further platitudes (like any hint to the dimensional analysis or even the pi-theorem by some ancients), in the vain course of explaining so called trivialities from first principles. Perhaps, mentioning transforming as co- and contra-variant would have spiced up the story. I deeply regret having done so! All Math is trivial tautologies. Purgy (talk) 07:27, 15 November 2017 (UTC)
- Now, now ... don't get your feathers ruffled. I respect, and use, formal generalized systematic concepts all the time. Where we might differ is along pedagogical grounds. I do not believe that that approach is always the best for introducing new concepts or explaining things to an audience not familiar with this way of thinking. You can counter that by saying that we are writing an encyclopedia and not a textbook and I will agree with that. However, for an encyclopedia to be useful, it must achieve understanding before it broadens to generalization. In other words, even though it is an encyclopedia, I believe that you need to work up to the most generalized statements and not start out with them. An encyclopedia that people can't use effectively is not much of an encyclopedia in my opinion. --Bill Cherowitzo (talk) 16:57, 15 November 2017 (UTC)
- To my IP friend. My apologies for my penultimate response; I thought I was responding to Purgy and not you. I am going to make one more attempt to show you that you are wrong (in the way you are thinking about this). If this approach does work, I am going to have to eat some crow and concede a few points to Purgy, so please let me know. Consider converting 1.5 to a percentage. You would want to write 1.5 × 100% = 150%. I would counter and say that 1.5 × 100% = 1.5. Now let's look at your computation in more detail. What you are doing is (1.5)(100%) = (1.5 × 100)% = 150%. I look at that and say that you are using the associative property of multiplication, namely a(bc) = (ab)c, and in order to do that you have to be considering % as a number. But, the point that Purgy is making (and I agree with, I just don't like the terminology) is that % is not a number but a unit, like sec., hr., mi., ounce, etc. In a computation, the units interact with other units and the numbers with other numbers and the twain shall never meet (this is a fundamental principle in dimensional analysis). So, in this computation we are considering, what is really going on is that 1.5 is being multiplied by 100 and then the unit (%) is attached. The fact that you can close your eyes to this, do it your way and get the right answer is just one of those schoolboy tricks where you do some bizarre manipulation of an expression and end up with a correct statement (there are tons of these). You can not justify the correctness of these tricks by claiming that you get the right answer! --Bill Cherowitzo (talk) 23:23, 15 November 2017 (UTC)
- Yay, we're friends! You apparently misunderstood me. I'm not trying to use the associative property of multiplication. I'm saying . I'm saying .
- The other points are interesting to debate, but not particularly important. If "%" can be used like units, then from follows that . Or, "%" can be used like a number, which would have to be defined as . I think my suggestion is correct for both schools of thought. By the way, you might want to read the first two sentences of dimensional analysis#Percentages_and_derivatives. --212.35.11.31 (talk) 23:01, 16 November 2017 (UTC)
- @212.35.11.31: Just to record my opinion: The first sentence pointed to, wrongly, reduces percentages to ratios of two dimensionally equal quantities, i.e. fails to mention rates, and, additionally, brushes over ratios with indeed equal dimension, but involving different units for this. The second sentence I dislike for involving the notion "add" wrt dimensions.
- Any expression validly equating "real" entities can be separated in one equation for their absolute measures and an other one for equating the employed units. Sometimes one or both equations are trivial. The use of percentages in pure math appears to me as negligible compared to the some (unit) interval.
- I insist on estimating a discussion about different units for the dimension of unity more satisfactory than talking about different units (see link above to "Zählmaße") for dimensionless quantities. Apologies to the landlord if this is considered intrusive. Friendly regards. Purgy (talk) 07:41, 17 November 2017 (UTC)
- Well it looks like I'll be having turkey (instead of crow) for Thanksgiving after all. --Bill Cherowitzo (talk) 19:50, 18 November 2017 (UTC)
- ... Enjoy! :) Purgy (talk) 08:01, 19 November 2017 (UTC)
- Bon appetit! Honestly, I still don't see how one can both write AND . If the is required in the first equation, the second equation would have to be written as , no? Which would be obviously wrong! Now, you could say that "% Error" describes a unitless number, expressed in percentages. Using that notation, if we're dealing with an error of 5% we'd have to write . It follows that and thus , which would be very unintuitive notation for me. But perhaps I'm a weirdo not understanding notation - so maybe it'd be simpler to just ignore me :). --147.86.223.242 (talk) 20:29, 20 November 2017 (UTC)
- Apologies to 147.86.223.242, for not ignoring you, and to Bill Cherowitzo, for usurping (hopefully only slightly) your talk page. From my perspective there are primarily two ways to clean up the mess in the above denotation:
- First, is to write and remarking that this is an equation involving only absolute measures (with names in quotes), with the LHS denoting an absolute measure wrt the unit and the RHS involving absolute measures wrt the unit .
- Second, is to start at the definition in explicit units of "unity" (parenthesizing units)
- and only afterwards to convert the result to the desired unit according to its definition, like to yield
- Certainly, one is free to define
- Obviously, I am an afficionado of the second method, especially when it comes to make things crystal clear. Gobble-gobble. Purgy (talk) 14:32, 21 November 2017 (UTC)
- Addendum: Please, note that for a reasonable evaluation of the above subtraction the involved measures must refer to the same unit, and in this here case this very same unit is assumed for the denominator too, and such the units in enumerator and denominator cancel in a meaningful way to the unit , they do not vanish to nada, as is suggested by the highly traditional, but never the less misleading unitless. Purgy (talk) 14:50, 21 November 2017 (UTC)
- Apologies to 147.86.223.242, for not ignoring you, and to Bill Cherowitzo, for usurping (hopefully only slightly) your talk page. From my perspective there are primarily two ways to clean up the mess in the above denotation:
ArbCom 2017 election voter message
Hello, Wcherowi. Voting in the 2017 Arbitration Committee elections is now open until 23.59 on Sunday, 10 December. All users who registered an account before Saturday, 28 October 2017, made at least 150 mainspace edits before Wednesday, 1 November 2017 and are not currently blocked are eligible to vote. Users with alternate accounts may only vote once.
The Arbitration Committee is the panel of editors responsible for conducting the Wikipedia arbitration process. It has the authority to impose binding solutions to disputes between editors, primarily for serious conduct disputes the community has been unable to resolve. This includes the authority to impose site bans, topic bans, editing restrictions, and other measures needed to maintain our editing environment. The arbitration policy describes the Committee's roles and responsibilities in greater detail.
If you wish to participate in the 2017 election, please review the candidates and submit your choices on the voting page. MediaWiki message delivery (talk) 18:42, 3 December 2017 (UTC)
director circle
Hi, I just noticed two different definitions of director circle (= orthoptic of an ellipse). The second usage: ellipse (definition of an ellipse via a circle). May be, that I caused this confusion. Please, could You check and put it right ? --Ag2gaeh (talk) 15:19, 16 January 2018 (UTC)
- All the English references to director circle that I have found refer to the orthoptic of an ellipse. I did find one reference to this other usage where it was called a circular directrix (a special case of a more general construct involving two focal circles where one has zero radius). I can fix this, but was wondering if there is a more specific German equivalent that should be mentioned. --Bill Cherowitzo (talk) 22:34, 16 January 2018 (UTC)
- In German WIKI the circle used for the alternative definition of an ellipse is called "Leitkreis", in French "cercle directeur", in Spanish: "circunferencia principal", which all mean director circle. In German books "Leitkreis" is commonly used for the alternative definition of an ellipse, for example: Kleine Enzyklopädie Mathematik, 1977, Harri Deutsch Verlag, p. 194. Perhaps one should skip the term "director circle" within the (en:Wiki) ellipse definition in order to prevent confusion. --Ag2gaeh (talk) 07:39, 17 January 2018 (UTC)
- add.: The same problem exists for hyperbola, too. --Ag2gaeh (talk) 09:06, 17 January 2018 (UTC)
- In German WIKI the circle used for the alternative definition of an ellipse is called "Leitkreis", in French "cercle directeur", in Spanish: "circunferencia principal", which all mean director circle. In German books "Leitkreis" is commonly used for the alternative definition of an ellipse, for example: Kleine Enzyklopädie Mathematik, 1977, Harri Deutsch Verlag, p. 194. Perhaps one should skip the term "director circle" within the (en:Wiki) ellipse definition in order to prevent confusion. --Ag2gaeh (talk) 07:39, 17 January 2018 (UTC)
 Done ---Bill Cherowitzo (talk) 22:38, 17 January 2018 (UTC)
Done ---Bill Cherowitzo (talk) 22:38, 17 January 2018 (UTC)
Argument?
"Not an improvement; trying to make an argument in a caption.", improvement can be using different descriptive semantic variations to convey meaning when literally true in form. It's not arguing for or against any point. You said the above from my (Zeno's paradox article addition of) "Showing an infintesimal 'syncopation' to the remainder of distance or distance made", I think that is more of a description, we're speaking of a literal dictionary definition; it's a semantic variation of the literal context. Whether or not it indicates the fact at hand may be the argument. So that logically, I made no argument, it is up to you to argue that such statement is an argument, and how. So may I ask how it poses an argument? Nagelfar (talk) 17:25, 18 January 2018 (UTC)
- A diagram is a diagram, and a caption is a verbal description of what is indicated by the diagram. The use of abstruse terminology in a caption is indicative of trying to impose a particular viewpoint, that is, an interpretation, on the visual image. Advocating a viewpoint is making an argument. This was a useless addition in a caption. If you have a point to make, it belongs in the body of the article with appropriate citations. --Bill Cherowitzo (talk) 20:40, 18 January 2018 (UTC)
Similarity of the Parabolas
Hi, someone placed the mark "unreferenced" to the section on the similarity of the parabolas. If there is really need of a citation, please, could You add one ? I have no access to English books. Thank You ! --Ag2gaeh (talk) 16:29, 23 January 2018 (UTC)
Template:General geometry
I think the image for Template:General geometry should be removed because it doesn't add any comprehensible information to the template. It doesn't tell the reader how to project a sphere onto a plane (the reader probably wasn't interested in this anyway). Brian Everlasting (talk) 04:02, 28 January 2018 (UTC)
- I've responded on the appropriate talk page. --Bill Cherowitzo (talk) 04:08, 28 January 2018 (UTC)
Marx's "independent discoveries"
Marx's mathematical manuscripts are available at:
https://www.marxists.org/archive/marx/works/download/Marx_Mathematical_Manuscripts_1881.pdf
Judge for yourself the accuracy of "Engels' claim that Marx made "independent discoveries" is certainly justified."
Best, JS (talk) 14:46, 1 February 2018 (UTC)
- This should really have been put on talk page for the article and I will copy it there, but respond here. By asking that I judge the accuracy of a statement by looking at the primary source, you are asking me violate a basic Wikipedia principle. Editors are not to make judgments, only report on judgments made by experts in the secondary literature. I could not tell if the statement you objected to was an editor's opinion or a paraphrase of a secondary source. In the first case, removal is appropriate but not in the second case. Given the ambiguity, the appropriate response would have been to add the {{dubious}} maintenance tag to the passage and discuss the concern on the talk page. --Bill Cherowitzo (talk) 19:21, 1 February 2018 (UTC)
- I have copied your reply to the article talk page, and also replied. Best, JS (talk) 13:11, 2 February 2018 (UTC)
Reversion of Generating function edits
Did you intend to revert both of my edits, in different sections of the article made days apart? If you find any part of either edit to be an improvement, please do let me know, as I don't wish to be in an edit war. Please know that I tried hard to make these edits as appropriate as I could and am feeling somewhat dispirited that your response did not permit even a smidgen. 64.132.59.226 (talk) 12:55, 21 February 2018 (UTC)
- While I initially didn't realize that I would be reverting two edits, when I became aware of that I examined both edits separately. In the earlier edit, your attempt to provide clarification didn't really work as you introduced a new function without definition (unless your lowercase gamma was meant to be the gamma function) and appeared to change the intention of the section rather than clarify it. The other edit involved a curiosity that didn't really rise above the level of trivia. As neither edit was supported by a citation I had no way to correct or improve these additions and reverting was the most reasonable approach. --Bill Cherowitzo (talk) 18:37, 21 February 2018 (UTC)
- Thank you for your quick response and constructive criticism. The γ was intended to be an arbitrary constant. I did not intend to change the intention of that section, though I will work with your criticism that the new wording is not as clear as the text that it replaced. The current text in that section doesn't seem clear enough to me, so I will mull it over; hopefully coming up with some text that you will view favorably. For the decimal-expansion edit, I will see if I can locate a citation. 64.132.59.226 (talk) 20:44, 21 February 2018 (UTC)
My undo
You know the only reason I caught that revert of yours was because, only a few minutes before, I almost reverted that IP's edit myself, thinking somehow it was a ref tag ;-) Paul August ☎ 18:39, 23 February 2018 (UTC)
- And that was exactly what I did (thinking it was a ref tag), how embarrassing ;^( Thanks again for catching it. --Bill Cherowitzo (talk) 18:43, 23 February 2018 (UTC)
Ternary relation
From Ternary relation: An example of a ternary relation in elementary geometry is the collinearity of points.
But neither Line (geometry) nor Collinearity are operators. Should I create an isCollinear(p1, p2, p3) redirect with the Category:Ternary operations? The problem with many articles is that they cover operations, properties, etc. and the title obscures one aspect of the concept. Perhaps the collinearity article could state that it would at least be a ternary relation. Dpleibovitz (talk) 21:59, 24 February 2018 (UTC)
- You would need to keep the distinction between relations and operators much clearer. Your "isCollinear" example is a ternary relation, probably the one meant in the Ternary relation article, but it is not an operator or operation. Also, ternary really does mean three, isCollinear with four inputs is not a ternary relation. Relations have a boolean output while operations have an output in the set that the inputs come from (there is some disagreement about this but it is generally accepted). The only time the two concepts get confused is when you are operating on boolean inputs. I think the fix here would be to correct the Ternary relation article to make this example clearer, and I will do that.
- Might I ask what your modus operandi is for assigning these categories? As you may have noticed, I sometimes find your selections to be inappropriate and if I understood the method you are using I could probably be a bit more constructive with my edits. --Bill Cherowitzo (talk) 22:49, 24 February 2018 (UTC)
I updated my User:Dpleibovitz page to give a better idea of what I try to do as a Wikipedian. I like to unify (to the extent possible under WP:NOR), especially in my areas of cognitive science, computing science, mathematics (& logic and digital electronics), philosophy, and ever-so-slightly, physics - my father was a physicist. This topic presents a case study. Firstly, I have excellent skills as a systems architect in complex systems (telecommunications, software). This requires generalizing (over similar things) and often, refactoring. The word operator is ambiguous with Operator (computer programming), Operator (physics), Logical operator, Operator (mathematics) & Operation (mathematics). In these cases, there is much behind the concepts which is more similar than different. Same is true for words such as function, method, (sub)routine, and relation; and indirectly tuples. For example, a computing function with two parameters could be seen as being a binary operator (in programming), or taking a single two-tuple and relating it to the returned value - all computing functions (or operators) can be seen as defining a relation between the result and the n-tuple - how we view these realizations is up to interpretation or implementation. The function need not be boolean nor represent a predicate. In any case, the notions of arity runs across all these concepts in very similar ways. I'm working on a table to capture these. That is also why I like general (discipline/formality independent) categories to capture the similarities (understanding that formal categories must also exist that have specific formal properties). So, much of my work is in adding see also and disambiguation entries, as well as more general categories. I get into trouble when I step over formal properties (which I thank you and other editors for spotting). But I also like to complete existing categories. These are hard if an article mentions that colinearity could be a ternary relation, but has no entry in the general Category:ternary operations. Somehow, I want to add the entry into that category, if not by the original article, then perhaps by an appropriate redirect. Dpleibovitz (talk) 19:49, 26 February 2018 (UTC)
- I think that one of the difficulties you may be facing is that you are working from imperfect data. There is a huge variation in how well some of our articles are written and you are making choices based on the good faith assumption that the articles are accurate. I probably don't have to remind you of the difficulty in dealing with GIGO. In the ternary relation article, that example left out so much detail (I'm sure that the editor who put that in felt that the example was so obvious that only a hint needed to be given!) that I am not surprised that you couldn't find appropriate categorization. I hope that my rewrite makes this clearer. Also, you are operating on relatively thin NOR ice. It is my understanding that assigning categories requires the same kind of sourcing as articles do. I would suggest that when in some grey areas you might ask other editors for some input on the talk pages. --Bill Cherowitzo (talk) 04:23, 28 February 2018 (UTC)
Bisection method math style changes reverted
Hi, I have noticed that you reverted my changes in the Bisection method article. I have done those because I consider math symbols rendered as math instead of as plain text more readable. What is your reasoning behind the revert?
- This has been an issue, hotly debated, for many years. The use of inline <math>...</math> has been discouraged by many established math editors for several reasons. Due to the imperfect implementation of the LaTeX code, the rendering is not scaled to the surrounding text, the baseline does not correspond and the emphasis is overdone. This also changes dramatically depending upon the viewer's browser options (whether MathJax is enabled or not, for example) and the platform (desktop, mobile, etc.). These problems are fixable, but no one sees this happening at any point in the near future. I do understand your concern and I also do not like the sans serif font used for mathematical symbols. My solution is to use the math template {{math|...}} which changes the font and doesn't have the other problems mentioned above (but this is not a perfect solution as there are limitations on what can be done) for inline math and LaTeX for displayed math only. --Bill Cherowitzo (talk) 18:38, 4 March 2018 (UTC)
- Thank you for a thorough explanation. I was not aware of the debate and the existing best practices. I fully agree that the baseline for inline math could be misaligned and as a result the emphasis might be overdone. While I hope that LaTeX code rendering is going to improve, I will employ your suggestions meanwhile.
ref
greetings... You and the other editor are merely asserting "not reliable" source, for that ref, but not offering just how. Also, that source was already discussed and agreed upon, with consensus, and established some time ago. It seems more that you just don't like the ref cuz it doesn't seem to meet up to something like "Britannica" or something...but Wikipedia does not stipulate that it necessarily has to be so well-known to be "reliable". Learning.com is simply a teaching and student and academic website. And WP does not forbid such sites as sources, necessarily. And the statement is unsourced. So what's the big issue here? I always kneel to consensus (even if provably wrong), but let's not let "I don't like" be the real motivation to remove this thing. And forgetting that this is a WIKI...and no one editor "owns" any article...and respect other people's contributions. Regardless of personal tastes or likes. The burden is on YOU to prove that this site is so obviously "unreliable" and just an "advertisement"...and totally not usable. You simply have not done that. Assertions without actual facts and proof don't cut it. Regards. 71.246.98.233 (talk) 18:33, 20 March 2018 (UTC)
that source was already discussed and agreed upon, with consensus, and established some time ago
- and exactly where was that. I was certainly part of at least one discussion of this, and there was no consensus, in fact only the editor who put it in had anything positive to say and most of that sounded just like your diatribe above. As for being a reliable source, look at WP:RSVETTING. This will give you an idea of what I look at to determine if a source is reliable. The source you insist on fails in almost all categories. All your huffing and puffing does not change the fact that this is a "teaser ad" for the website and that is unacceptable for Wikipedia. --Bill Cherowitzo (talk) 18:54, 20 March 2018 (UTC)- I agree with that analysis. The talk page discussion was most definitely not in favour of including this ref, this IP does sound much like that previous supporter (and somewhat suspiciously added the ref with the old access date still intact), and the ref is not reliable. Meters (talk) 05:17, 21 March 2018 (UTC)
- since when is a learning academic website, with credentialed teachers on the site, forbidden outright on Wikipedia, and dogmatically considered an "unreliable source"? 71.246.98.233 (talk) 16:47, 21 March 2018 (UTC)
- I agree with that analysis. The talk page discussion was most definitely not in favour of including this ref, this IP does sound much like that previous supporter (and somewhat suspiciously added the ref with the old access date still intact), and the ref is not reliable. Meters (talk) 05:17, 21 March 2018 (UTC)
I am copying this discussion to the Talk:Sphere page where it belongs. --Bill Cherowitzo (talk) 18:00, 22 March 2018 (UTC)
What's your problem ?
Recently I shared my proves at "Regualr Polygon"
What's your problem? What's poorly written? Are you stupid or what? I took 2 hours to write stuff and you delete it in one second. Here what: Go to hell and piss of! I don't care if Ill be banned from Wiki. If this is the community of wikipedia, then it sucks. Because I came here not for spending time on nothing! — Preceding unsigned comment added by Anatoly Wein (talk • contribs) 18:01, 21 April 2018 (UTC)
- I am sorry that you feel that way, but you really should have taken some time to read Wikipedia policies before plunging right in to add material. One of those policies is WP:NOR which in essence says that we do not accept material that is not published in reliable sources already. If you want your "proofs" to appear on Wikipedia you would need to get them published first and accepted by the mathematical community. As to the quality of your English, I count at least 6 mistakes in the short entry above and the article was much worse. Non-native speakers of English contribute to Wikipedia all the time and this causes no problems in general because other editors will smooth out the language problems. This requires a certain amount of understanding and cooperation on both sides and a willingness to learn from our mistakes. --Bill Cherowitzo (talk) 18:25, 21 April 2018 (UTC)
Why? Wikipedia is just worse if you don't allow my proves to appear. I spend 2 hours time on releasing my proves. All you do is reverting them. Congratulations! You're all bad. "Ill delete your stuff you took 15 hours on editing. Sorry." Sorry but Wikipedia is idiotically bad.
Reversion of Squaring the circle
The edit I added filled in a missing step in my understanding of why this is impossible. If I received permission from my professor to post the transcript online (e.g. a blog) and I refer to that would it be acceptable? He is a professor at a major state university after all. His credibility is important to him so he wouldn’t take the claim lightly. Does Wikipedia ironically only accept traditionally published experts? Chidedneck (talk) 06:21, 28 April 2018 (UTC)
- One of the pillars of Wikipedia is verifiability. Readers need to be able to find the source of a statement in reliable secondary sources and an editor's job is to direct readers to these. Blogs, which is what your posting of this interview would be as you say, create problems in this regard and are generally to be avoided (see WP:BLOGS). That is not to say that they necessarily contain errors or are not to be trusted, far from it, most blogs have good quality information. The problem is that in order to trust the information in a blog one has to trust the author of the blog. How is this trust to be established? A recognized authority (recognized by many people in the appropriate field) can be given this trust, but a person who just claims that they know the material has not earned this trust unless their work has been vetted by the, in this case, mathematical community. In academia these bona fides are established by publication in scholarly outlets. So the answer to your last question is yes in any academic area.
- Turning now to the specifics of my edit, there were two statements made in the sentence. One was that this information was known years before Lindemann proved the transcendental nature of π and the second was the mathematical framework of that information. For a quote of an individual to support the first claim, they would have to be a mathematical historian. The second claim is considerably easier and can be found in many texts, so referring to a specialist would seem to be overkill.--Bill Cherowitzo (talk) 20:41, 28 April 2018 (UTC)
I think you may have misread my edit. It did not claim that "this information was known years before Lindemann proved the transcendental nature of π". It did confirm that a geometric diagram starting with a unit circle which would otherwise demonstrate that squaring the circle is possible, is in fact not possible due to the fact that since 1 is an algebraic number it can only lead to other algebraic numbers. The reverted text makes an unsupported claim when it says: "It had been known for some decades before then that the construction would be impossible if π were transcendental". My edit was an attempt to close the logical gap left by "it was known" by citing my math professor. I concede the point about vetted secondary sources being the ideal sources, you're right. The geometric figure was: Chidedneck (talk) 06:14, 29 April 2018 (UTC)
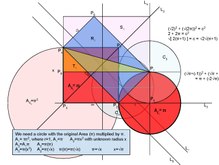
- Augustus De Morgan's A Budget of Paradoxes contains many "proofs" of circle squaring, all of which are of course flawed in some way. The reasoning you've applied above can be used for each of these, so the question arises, in what way does the argument of this diagram rise above these others? While your edit did remove the specific time duration (years), it did not eliminate the sense of the statement and would still need a citation. --Bill Cherowitzo (talk) 04:28, 29 April 2018 (UTC)
Center
Stop spelling center wrong. I know it is the British way, but the makes no pronunciation sense. The Clorax (talk) 00:27, 30 April 2018 (UTC)
- Wrong is in the eye of the beholder! We try to respect the fact that English comes in different varieties and none of them is better or worse than another. I do not use British spellings, but when I come across it I respect the work of other editors who do. I'd suggest that you learn how to be more tolerant of these differences.--Bill Cherowitzo (talk) 02:46, 30 April 2018 (UTC)
Ignoring is not a way.
https://en.wikipedia.org/w/index.php?title=Regular_polygon&oldid=837566468
revert it finally. I took myself 2 hours! How can you tell me that you have any idea in maths. If you really rejected this, then you're noobish in maths! You're helpless. Old veteran finding it funny to remove my proves...
STUPID!
- Anatoly, please remember to sign your posts (by typing four tildes ~~~~). We try to remain civil in our posts; name-calling and rudeness are just signs of immaturity. I have explained (above) why I reverted your edit, and as far as I can tell nothing has changed in that regard. The only thing that I find funny in this situation is your continued misspelling of the word proof. --Bill Cherowitzo (talk) 19:41, 1 May 2018 (UTC)
Trusting Sources
You have reverted the inclusion of two books ("best sellers" in France) dealing with the problem of the Infinite in Sciences (mathematics and astronomy). I am new in Wikipedia, after using it for many years as a passive reader I decided that now is time to help other readers. I have a PhD in Physics, professor at the University, and also working a lot with history of sciences. Instead of reverting again your deletion, I prefer you get convinced of my modification and include it again in the article. The books have an ISBN, and I verified that they are at WorldCat, and even for sale in Amazon (USA, France, Canada). So, please, tell me what are the factors that make you believe are not verified sources. Start from the title, contributors, references, etc. You can argue they are in French and this article is in English, but nowadays you need to understand many languages if you want to know more about science. I myself understand/write/read in English, Spanish, and French. Thank you for any advice you can give me. And, after you are convinced, please revert my modifications in the article on Infinite. Thank you! Triboscience (talk) 00:49, 4 May 2018 (UTC) — Preceding unsigned comment added by Triboscience (talk • contribs) 00:42, 4 May 2018 (UTC)
- We generally put new comments at the end of a talk page (unlike most other places on the web) so I have taken the liberty of moving yours here.
- As to the books. Firstly, anyone can obtain an ISBN for a book, so having one says nothing about the quality of the work. Secondly, I also checked OpenCat and their listing claimed that the author was unknown and this made me very suspicious. Finally, and perhaps most importantly, references are listed that provide support for statements made in the article, and there was nothing in the article that these books were being used for. Wikipedia is not an indiscriminate collection of facts or references, there must be a reason to refer to something. The fact that the books are in French is not a problem, but because they are I was unable to use other factors that I normally rely upon to determine if a source is reliable. Given the nature of the topic and the fact that it attracts many crank publications I felt that it was safest to revert until more information was available. The books were listed in a ==Further reading== section (which was unfortunately called ==Sources==), but to do that it would be necessary to have a scholarly review of the books to show that they contain important information concerning the topic. The WorldCat listings had no ratings and no reviews for either book. If you can shed more light on this I will be happy to reconsider.--Bill Cherowitzo (talk) 03:36, 4 May 2018 (UTC)
- @Triboscience: see also [1]. - DVdm (talk) 08:09, 4 May 2018 (UTC)
{{subst:DRN-notice|topic|noticeboard=noticeboard|reason=a very important statement, supported by numerous outside reliable sources and by Wikipedia itself. the section i added described the important work of Sharaf al-Dīn al-Ṭūsī and his contribution to the development of the function.ive added the sources as requested but the subject was Abandoned. the sources show clearly,the early stages of the method.i also want to add al Bruni contribution at the same section supported by another source ill provide.|thread=https://en.wikipedia.org/wiki/Talk:History_of_the_function_concept#Sharaf_al-D%C4%ABn_al-%E1%B9%AC%C5%ABs%C4%AB}}--~~~~
Reversion of Binomial coefficient:Identities
Dear Wcherowi, was there anything wrong with the formula I added to the section Binomial coefficient:Identities involving binomial coefficients ?
In the formula m is an integer less or equal to n, as h few lines above (it is also unspecified). Also, I don't see any citation for the formulae above.
--Gim²y (talk) 15:15, 1 May 2018 (UTC)
- I did not claim that there was anything wrong with the formula you provided, my objection was primarily that this looked like your own work. One of the things that led me to that suspicion was the use of m that appears only on the LHS of the formula and so needs to be specified (or quantified). This is unlike the h of an earlier formula that appears on both sides of the identity and is therefore a free variable. Published work would not be so sloppy in their presentations. Wikipedia does not publish the original work of its editors (see WP:NOR)–a fact that Anatoly (below) does not seem to appreciate). While you correctly point out that earlier identities did not have citations, this is not a reason why your entry should not have a citation. These earlier formulae are all standard identities and could easily (and should) be cited. If I am wrong about this being original work, a simple citation would clarify that situation. --Bill Cherowitzo (talk) 19:19, 1 May 2018 (UTC)
- Dear Bill Cherowitzo, you are completely right. I am sorry, I was a bit sloppy. I first looked up for such a formula in the literature, but I was not able to find it quickly. Then I computed it, and I realized that it follows quite immediately from the definition of binomial coefficient. As you said, it should easily be cited, or, at least, verified. Let me explain the first formula first. Clearly for every . Writing in this way immediately gives the first formula I added, from the one at the beginning of the section. For the second one, let m be an integer such that . Then, by definition of binomial coefficient, we have and the factor is exactly what is missing in order to obtain . Of course, if now these formulae turn out to be too obvious for the article, I apologie for my previous edit. Gim²y (talk) 23:40, 13 May 2018 (UTC)
- He removed even my proves: He has no idea about maths. — Preceding unsigned comment added by Anatoly Wein (talk • contribs) 16:21, 1 May 2018 (UTC)
Revert of combinatorial proof for Chu–Vandermonde identity (alternative form)
Hi Bill, thanks for your review of my edits to Binomial coefficient.
This is one of my first edits, so not sure what is appropriate where. I see you reverted the change, marking it as "good faith" (which if I understand correctly is saying you believe the edits were done in good faith) and with the comment "Unsourced and not quite correct".
As background, what happened was that I came across a math problem that required an application of the above identity, which I was not familiar with, and which I then found on this wikipedia page. However, I could not find a simple combinatorial proof for it even though I thought it seemed like there should be one. I searched for Chu-Vandermonde identity and could not even find other references to this form of the identity but only the main one (Identity 9 - the one marked as an alternate form of the main Chu-Vandermonde identity). So I found a combinatorial proof of the hockey stick identity and then constructed a combinatorial proof of identity 9 myself, along similar lines, because I thought it could be helpful to others. I also asked a friend to verify my proof for readability and correctness, to lower the risk of posting something wrong (though I knew it would be reviewed).
So, my questions are:
- What were the errors you saw in the proof? (this would be useful to me even if the end result is not publishing the changes to the page)
- As you see above, I cannot cite a source for the proof because I couldn't find one and had to construct it myself (which is why I thought it might be helpful to others). Does this mean the material should not be added to the page, or should it be re-added once I fix any errors you point out?
- Assuming the material should be added, maybe a better place for it would be under the "Identities with combinatorial proofs" section?
thanks Ronnie Ronniemaor (talk) 14:43, 4 June 2018 (UTC)
- Hi Ronnie, the mistake I saw in the proof had to do with the condition "if the j + 1-st item selected for the subset is m ...". For this to make sense you have to be constructing ordered subsets and that would throw the whole count off (you could try imposing an order and then dividing out by the appropriate factorial to get back to unordered sets, a technique that sometimes works well but can be a bit delicate). Putting aside the math question, your proof, even if corrected, could not be used in a Wikipedia article. Being unsupported by the literature means that it would be considered original research (see WP:OR) and Wikipedia does not publish such–this is one of the core principles underlying Wikipedia. The identity itself (although probably not under this name) appears frequently in combinatorics texts, although often as an exercise. --Bill Cherowitzo (talk) 17:09, 4 June 2018 (UTC)
- Thanks Bill, I probably wasn't clear about the wording. I impose an arbitrary ordering on the original group's elements and then use that ordering to partition the counting of unordered subsets (I think that's what you mention above, and I think that's what I did). Anyway, it's a shame I can't share it to make the material more understandable, but I guess I can understand where those rules come from. Cheers and thanks again for the comments Ronniemaor (talk) 18:21, 4 June 2018 (UTC)
A series of facts.
A series of facts is what you deleted while calling it "undocumented opinion". Definitions of "===" in the Ruby programming language are not opinions, they are definitions. There is no use of the "===" operator in the standard classes that matches the mathematical definition of "set inclusion". If you can't verify that fact using the interpreter, there is also a reference manual. If citation is needed, then add a "citation needed" tag. :-((( Matju2 (talk) 01:05, 26 June 2018 (UTC)
- To be precise, your "series of facts" that I deleted is
In reality, === does not do "set inclusion". What's Gillette's ("why's") book actually means is that it tests for membership in some set, for some classes of left-hand values. By default, === does the same as ==, and this default also applies to many types that otherwise could have been considered as sets of some kind, such as Arrays and Hashes. The reason for the existence of === is as way to define case...when...else...end expressions (called "switch statements" in several other languages) in a more convenient way than if it had used ==, but that possibility was only really used for a small portion of classes, chiefly Range, Regexp, Module/Class, though it can be extended at will to user-defined types.
Now,
- "
In reality, === does not do set inclusion.
" implies that you are claiming something in a written source is not true in practice. This is not a paraphrase of what is in the source, it is your opinion. - "
What's Gillette's ("why's") book actually means is...
", again you are interpreting what is in a given source, ... that is opinion and not fact. - "
The reason for the existence of === is as way to define ...
", unless you are an originator of the Ruby language or are sourcing such a person, this is your interpretation of why this symbol was introduced, again opinion, not fact. - I am not saying that your contribution was incorrect, but just supplying a citation would not be enough to fix the problems that I see with it. This needs to be written better and a source that says these things must be cited. Just interpreting the user manual does not suffice.--Bill Cherowitzo (talk) 03:31, 26 June 2018 (UTC)
« Case Equality – For class Object, effectively the same as calling #==, but typically overridden by descendants to provide meaningful semantics in case statements. »[2] ; « Returns true if obj is an element of the range, false otherwise. Conveniently, === is the comparison operator used by case statements. » [3] which means set membership, not set inclusion. If you test (2..5)===(3..4), it returns false, because the subrange 3..4 is not an element of 2..5. The output of the interpreter is not my opinion. Gillette's book has an error in it and Wikipedia is citing this error. Also, the easiest way to look at the list of all standard definitions of === is to install Ruby and look for just "===" in ri (in a Linux or OSX terminal you'd type just "ri ==="). There you see that all of them are either plain equality, or set membership for some definition of set. But there seems to be no online (http url) equivalent. BTW, I got no notification, I was just making sure you hadn't replied and found you had done so days ago already. Matju2 (talk) 20:12, 29 June 2018 (UTC)
- @Matju2: Let me state again, perhaps more positively, I do not disagree with anything you have said. The problems here involve how you write for an encyclopedia and how you support what you've written. You are not writing for fellow specialists but for a more general readership. This means that you have to be more careful in how you say things, so as not to accidentally slip into jargon or make the usual assumptions you would make in typical writing for your peers. The voice you use in Wikipedia can not be your own voice, it must be that of some reliable source. You can not just tell the reader to "go do this and you will clearly see that ..." as this is asking readers to make their own conclusions and is not reporting, as an encyclopedia should, on what the experts have concluded. You have stated that Why's book has an error in it (I believe you are correct in that) and there are two ways to go about correcting this. The first is to find a reliable source that points out this error and cite that source, or, if that doesn't seem possible, discuss on the talk page of the article the problem and ask for consensus to remove the incorrect statement. --Bill Cherowitzo (talk) 20:08, 30 June 2018 (UTC)
reversion
I don't agree with this revert[4]: can you explain? I don't understand the significance of the edit summary and the Cramér model being "conjecture". Of course the distribution of primes isn't really random. The link to the Cramér model was just to show that the "random" model has some history and is used for some calculations like this. The section is about a heuristic guess about Fermat primes that doesn't pretend to be rigorous. The Cramér model is not "conjectured": it's outright false if taken as a precise statement. It's simply being used as a heuristic approximation, and is the usual name for the random model described in the Fermat prime article.
The Cramér conjecture (about gaps between primes) is not the same thing as the Cramér model, if that's the "conjecture" you were objecting to. Rather, the model is heuristic evidence for the conjecture (and similarly for there being a finite number of Fermat primes). The pipelink to Cramér model was the right thing because that's a more precise name for the heuristic presumption that the primes are distributed randomly according to the PNT. 173.228.123.166 (talk) 03:50, 17 July 2018 (UTC)
Added: see here for more info. 173.228.123.166 (talk) 03:56, 17 July 2018 (UTC)
- Ok. First an apology, I didn't mean to say "conjectured model", what I had in mind was "a conjecture's model", but it didn't come out that way. But the real underlying reason for the revert had two components. The first was the issue of the link being too technical and the second, somewhat related issue was the principle of "least surprise". As I read the passage, the level of exposition seemed to call for an elementary link to the concept of randomness and a reader hitting that link with that expectation would clearly be befuddled by a description of a heuristic that happens to be used in these circumstances. The way to fix this would be to leave the link to randomness and then briefly expand on how randomness is dealt with in the Fermat prime setting. This discussion would probably be better placed on the article's talk page, where other editors could toss in their two cents worth. --Bill Cherowitzo (talk) 02:07, 20 July 2018 (UTC)
































