Snub order-8 triangular tiling
| Snub order-8 triangular tiling | |
|---|---|
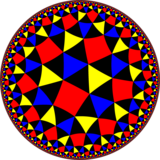
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | 3.3.3.3.3.4 |
| Schläfli symbol | s{3,8} s(4,3,3) |
| Wythoff symbol | | 4 3 3 |
| Coxeter diagram | |
| Symmetry group | [8,3+], (3*4) [(4,3,3)]+, (433) |
| Dual | Order-4-3-3 snub dual tiling |
| Properties | Vertex-transitive |
In geometry, the snub tritetratrigonal tiling or snub order-8 triangular tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbols of s{(3,4,3)} and s{3,8}.
Images
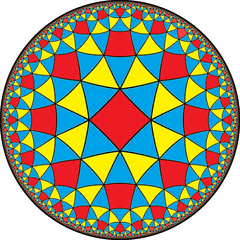
Drawn in chiral pairs:
Symmetry
The alternated construction from the truncated order-8 triangular tiling has 2 colors of triangles and achiral symmetry. It has Schläfli symbol of s{3,8}.
Related polyhedra and tiling
| Symmetry: [(4,3,3)], (*433) | [(4,3,3)]+, (433) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

| |||
| h{8,3} t0(4,3,3) |
r{3,8}1/2 t0,1(4,3,3) |
h{8,3} t1(4,3,3) |
h2{8,3} t1,2(4,3,3) |
{3,8}1/2 t2(4,3,3) |
h2{8,3} t0,2(4,3,3) |
t{3,8}1/2 t0,1,2(4,3,3) |
s{3,8}1/2 s(4,3,3) | |||
| Uniform duals | ||||||||||

|

|

|

|

|

|

|

| |||
| V(3.4)3 | V3.8.3.8 | V(3.4)3 | V3.6.4.6 | V(3.3)4 | V3.6.4.6 | V6.6.8 | V3.3.3.3.3.4 | |||
| Uniform octagonal/triangular tilings | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [8,3], (*832) | [8,3]+ (832) |
[1+,8,3] (*443) |
[8,3+] (3*4) | ||||||||||
| {8,3} | t{8,3} | r{8,3} | t{3,8} | {3,8} | rr{8,3} s2{3,8} |
tr{8,3} | sr{8,3} | h{8,3} | h2{8,3} | s{3,8} | |||
| Uniform duals | |||||||||||||
| V83 | V3.16.16 | V3.8.3.8 | V6.6.8 | V38 | V3.4.8.4 | V4.6.16 | V34.8 | V(3.4)3 | V8.6.6 | V35.4 | |||
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.