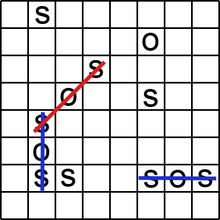
SOS is paper and pencil game for two or more players. It is similar to tic-tac-toe and dots and boxes, but has much greater complexity.^[1]

SOS is a combinatorial game when played with two players. In terms of game theory, it is a zero-sum, sequential game with perfect information.

Before play begins, a square grid of at least 3×3 squares in size is drawn. Players take turns to add either an "S" or an "O" to any square, with no requirement to use the same letter each turn. The object of the game is for each player to attempt to create the straight sequence S-O-S among connected squares (either diagonally, horizontally, or vertically), and to create as many such sequences as they can. If a player succeeds in creating an SOS, that player immediately takes another turn, and continues to do so until no SOS can be created on their turn. Otherwise turns alternate between players after each move.^[2][3]

Keeping track of who made which SOSs can be done by, e.g., one player circling their SOSs and the other player drawing a line through theirs. Once the grid has been filled up, the winner is the player who made the most SOSs.^[3][4][5] If the grid is filled up and the number of SOSs for each player is the same, then the game is a draw.

The game can also be played where the player who creates an SOS is the winner and if no SOSs are created the game is a draw.^[6]

• "An Assortment of Combinatorial Games," pg. 8, at Prof. Hugh L. Montgomery's University of Michigan website. Also available in PostScript format.