Lute of Pythagoras
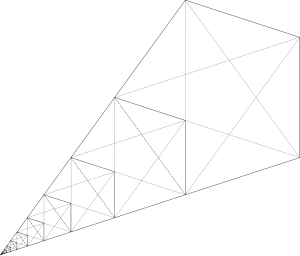
The lute of Pythagoras is a self-similar geometric figure made from a sequence of pentagrams.
Constructions
The lute may be drawn from a sequence of pentagrams. The centers of the pentagrams lie on a line and (except for the first and largest of them) each shares two vertices with the next larger one in the sequence.[1][2]
An alternative construction is based on the golden triangle, an isosceles triangle with base angles of 72° and apex angle 36°. Two smaller copies of the same triangle may be drawn inside the given triangle, having the base of the triangle as one of their sides. The two new edges of these two smaller triangles, together with the base of the original golden triangle, form three of the five edges of the polygon. Adding a segment between the endpoints of these two new edges cuts off a smaller golden triangle, within which the construction can be repeated.[3][4]
Some sources add another pentagram, inscribed within the inner pentagon of the largest pentagram of the figure. The other pentagons of the figure do not have inscribed pentagrams.[3][4][5]
Properties
The convex hull of the lute is a kite shape with three 108° angles and one 36° angle.[2] The sizes of any two consecutive pentagrams in the sequence are in the golden ratio to each other, and many other instances of the golden ratio appear within the lute.[1][2][3][4][5]
History
The lute is named after the ancient Greek mathematician Pythagoras, but its origins are unclear.[3] An early reference to it is in a 1990 book on the golden ratio by Boles and Newman.[6]
See also
References
- ^ a b Gullberg, Jan (1997), Mathematics: From the Birth of Numbers, W. W. Norton & Company, p. 420, ISBN 9780393040029.
- ^ a b c Darling, David (2004), The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes, John Wiley & Sons, p. 260, ISBN 9780471667001.
- ^ a b c d Lamb, Evelyn (May 29, 2013), "Strumming the Lute of Pythagoras", Scientific American.
- ^ a b c Ellison, Elaine Krajenke (2008), "Create a Mathematical Banner Using the Lute, the Sacred Cut, and the Spidron", Bridges Leeuwarden: Mathematics, Music, Art, Architecture, Culture, pp. 467–468, ISBN 9780966520194.
- ^ a b Pickover, Clifford A. (2011), A Passion for Mathematics: Numbers, Puzzles, Madness, Religion, and the Quest for Reality, John Wiley & Sons, pp. 331–332, ISBN 9781118046074.
- ^ Boles, Martha; Newman, Rochelle (1990), The Golden Relationship: Universal patterns, Pythagorean Press, pp. 86–87, ISBN 9780961450434.
