Lattice Miner
Lattice Miner [1] is a formal concept analysis software tool for the construction, visualization and manipulation of concept lattices. It allows the generation of formal concepts and association rules as well as the transformation of formal contexts via apposition, subposition, reduction and object/attribute generalization, and the manipulation of concept lattices via approximation, projection and selection. Lattice Miner allows also the drawing of nested line diagrams.
Introduction
Formal concept analysis (FCA) is a branch of applied mathematics based on the formalization of concept and concept hierarchy and mainly used as a framework for conceptual clustering and rule mining.[2] Over the last two decades, a collection of tools have emerged to help FCA users visualize and analyze concept lattices.[3][4] They range from the earliest DOS-based implementations (e.g., ConImp and GLAD) to more recent implementations in Java like ToscanaJ,[5] Galicia,[6] ConExp [7] and Coron.[8] A main issue in the development of FCA tools is to visualize large concept lattices and provide efficient mechanisms to highlight patterns (e.g., concepts, associations) that could be relevant to the user. The initial objective of the FCA tool called Lattice Miner [9] was to focus on visualization mechanisms for the representation of concept lattices, including nested line diagrams. Later on, many other interesting features were integrated into the tool.
Functional architecture of Lattice Miner
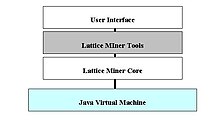
Lattice Miner is a Java-based platform whose functions are articulated around a core. The Lattice Miner core provides all low-level operations and structures for the representation and manipulation of contexts, lattices and association rules. Mainly, the core of Lattice Miner consists of three modules: context, concept and association rule modules. The user interface offers a context editor and concept lattice manipulator to assist the user in a set of tasks. The architecture of Lattice Miner is open and modular enough to allow the integration of new features and facilities in each one of its components.
Context module

The context module offers all the basic operations and structures to manipulate binary and valued contexts as well as context decomposition to produce nested line diagrams. Basic context operations include apposition, subposition, generalization, clarification, reduction as well as the complementary context computation. The module provides also the arrow relations (for context reduction and decomposition) [2]. The tool has an input LMB format and recognizes the binary format SLF found in Galicia and the format CEX produced by ConExp.
Concept module

The main function of the concept module is to generate the concepts of the current binary context and construct the corresponding lattice and nested structure (see Figures 2 and 3). It provides the user with basic operators such as projection, selection, and exact search as well as advanced features like pair approximation. Some known algorithms are included in this module such as Bordat’s procedure, Godin’s algorithm and NextClosure algorithm.[10] The approximation feature implemented in Lattice Miner is based on the following idea: given a pair (X,Y) where X ⊆ G, and Y ⊆ M, is there a set of formal concepts (Ai,Bi) which are “close to” (X,Y)? To answer this question, The tool starts to identify the type of couple that the pair (X,Y) represents.[11] It can be a formal concept, a protoconcept, a semiconcept or a preconcept. In the last case, the approximation is given by the interval [(X",X′),(Y′,Y")] and highlighted in the line diagram.
Association rule module
This module includes procedures for computing the (stem) Guigues–Duquenne base using NextClosure algorithm [3], as well as the generic and informative bases. Implications with negation can be obtained using the apposition of a context and its complementary. This module embeds also procedures for the computation of a non-redundant family C of implications and the closure of a set Y of attributes for the given implication set C.
User interface
The initial objective of Lattice Miner was to focus on lattice drawing and visualization either as a flat or nested structure by taking into account the cognitive process of human beings and known principles for lattice drawing (e.g., reducing the number of edge intersections, ensuring diagram symmetry). Some well-known visualization techniques were implemented such as focus & context and fisheye view. The basic idea behind focus & context visualization paradigm is to allow a viewer to see key (important) objects in full detail in the foreground (focus) while at the same time an overview of all the surrounding information (context) remains available in the background. Lattice Miner translates the focus & context paradigm into clear and blurred elements while the size of nodes and the intensity of their color were used to indicate their importance. Various forms of highlighting, labelling and animation are also provided.

In order to better handle the display of large lattices, nested line diagrams are offered in the tool. Figure 3 shows the third level of the nested line diagram corresponding to the binary context of Figure 1 where three levels of nesting are defined. Each one of the inner nodes of this diagram represents a combination of attributes from the previous two (outer) levels. Real inner concepts (see the node on the left hand-side of the diagram) are identified by colored nodes while void elements are in grey color. Each node of levels 1 and 2 can be expanded to exhibit its internal line diagram. Both flat and nested diagrams can be saved as an image. Simple (flat) lattices can also be saved as an XML format file.
References
- ^ Boumedjout Lahcen and Leonard Kwuida. Lattice Miner: A Tool for Concept Lattice Construction and Exploration. In Supplementary Proceeding of International Conference on Formal concept analysis (ICFCA'10), 2010
- ^ Bernhard Ganter and Rudolf Wille. Formal Concept Analysis: Mathematical Foundations. Springer-Verlag New York, Inc., 1999.
- ^ Thomas Tilley. Tool support for fca. In ICFCA, pages 104–111, 2004.
- ^ Pascal Hitzler and Henrik Schärfe. Conceptual Structures in Practice. studies in informatics series. CRC Press, 2009.
- ^ Peter Becker and Joachim Hereth Correia. The toscanaj suite for implementing conceptual information systems. In Bernhard Ganter and Gerd Stumme, editors, Formal Concept Analysis, volume 3626 of Lecture Notes in Computer Science, pages 324–348. Springer Berlin / Heidelberg, July 2005.
- ^ Petko Valtchev, David Grosser, Cyril Roume, and Mohamed Rouane Hacene. Galicia: An open platform for lattices. In In Using Conceptual Structures: Contributions to the 11th Intl. Conference on Conceptual Structures (ICCS03, pages 241–254. Shaker Verlag, Herzogenrath 2003.
- ^ Concept explorer. http://conexp.sourceforge.net/license.html.
- ^ Laszlo Szathmary and Amedeo Napoli. Coron: A framework for levelwise itemset mining algorithms. In Supplementary Proceedings of the Third International Conf. on Formal Concept Analysis (ICFCA’05), Lens, pages 110–113, 2005.
- ^ Geneviève Roberge. Visualisation des résultats de la fouille des données dans les treillis des concepts. Master’s thesis, Université du Québec en Outaouais, 2007.
- ^ Bernhard Ganter. Two basic algorithms in concept analysis. Preprint 831, Technische Hochschule Darmstadt, June 1984.
- ^ Rokia Missaoui, L´eonard Kwuida, Mohamed Quafafou, and Jean Vaillancourt. Algebraic operators for querying pattern bases. CoRR, abs/0902.4042, 2009. Also published in the Supplementary proceedings of ICFCA’2009, pp. 1–17, Darmstadt, Germany, May 2009.
