Langbahn Team – Weltmeisterschaft

Knowledge graph embedding

Embedding of a knowledge graph. The vector representation of the entities and relations can be used for different machine learning applications.

In representation learning, knowledge graph embedding (KGE), also referred to as knowledge representation learning (KRL), or multi-relation learning,[1] is a machine learning task of learning a low-dimensional representation of a knowledge graph's entities and relations while preserving their semantic meaning.[1][2][3] Leveraging their embedded representation, knowledge graphs (KGs) can be used for various applications such as link prediction, triple classification, entity recognition, clustering, and relation extraction.[1][4]

Definition

A knowledge graph is a collection of entities , relations , and facts .[5] A fact is a triple that denotes a link between the head and the tail of the triple. Another notation that is often used in the literature to represent a triple (or fact) is . This notation is called resource description framework (RDF).[1][5] A knowledge graph represents the knowledge related to a specific domain; leveraging this structured representation, it is possible to infer a piece of new knowledge from it after some refinement steps.[6] However, nowadays, people have to deal with the sparsity of data and the computational inefficiency to use them in a real-world application.[3][7]

The embedding of a knowledge graph translates each entity and relation of a knowledge graph, into a vector of a given dimension , called embedding dimension.[7] In the general case, we can have different embedding dimensions for the entities and the relations .[7] The collection of embedding vectors for all the entities and relations in the knowledge graph can then be used for downstream tasks.

A knowledge graph embedding is characterized by four different aspects:[1]

  1. Representation space: The low-dimensional space in which the entities and relations are represented.[1]
  2. Scoring function: A measure of the goodness of a triple embedded representation.[1]
  3. Encoding models: The modality in which the embedded representation of the entities and relations interact with each other.[1]
  4. Additional information: Any additional information coming from the knowledge graph that can enrich the embedded representation.[1] Usually, an ad hoc scoring function is integrated into the general scoring function for each additional information.[5][1][8]

Embedding procedure

All the different knowledge graph embedding models follow roughly the same procedure to learn the semantic meaning of the facts.[7] First of all, to learn an embedded representation of a knowledge graph, the embedding vectors of the entities and relations are initialized to random values.[7] Then, starting from a training set until a stop condition is reached, the algorithm continuously optimizes the embeddings.[7] Usually, the stop condition is given by the overfitting over the training set.[7] For each iteration, is sampled a batch of size from the training set, and for each triple of the batch is sampled a random corrupted fact—i.e., a triple that does not represent a true fact in the knowledge graph.[7] The corruption of a triple involves substituting the head or the tail (or both) of the triple with another entity that makes the fact false.[7] The original triple and the corrupted triple are added in the training batch, and then the embeddings are updated, optimizing a scoring function.[5][7] At the end of the algorithm, the learned embeddings should have extracted the semantic meaning from the triples and should correctly predict unseen true facts in the knowledge graph.[5]

Pseudocode

The following is the pseudocode for the general embedding procedure.[9][7] 

algorithm Compute entity and relation embeddings is
    input: The training set , 
           entity set , 
           relation set ,     
           embedding dimension 
    output: Entity and relation embeddings

    initialization: the entities  and relations  embeddings (vectors) are randomly initialized

    while stop condition do
         // From the training set randomly sample a batch of size b
        for each  in  do
              // sample a corrupted fact of triple
             
        end for
        Update embeddings by minimizing the loss function
    end while

Performance indicators

These indexes are often used to measure the embedding quality of a model. The simplicity of the indexes makes them very suitable for evaluating the performance of an embedding algorithm even on a large scale.[10] Given as the set of all ranked predictions of a model, it is possible to define three different performance indexes: Hits@K, MR, and MRR.[10]

Hits@K

Hits@K or in short, H@K, is a performance index that measures the probability to find the correct prediction in the first top K model predictions.[10] Usually, it is used .[10] Hits@K reflects the accuracy of an embedding model to predict the relation between two given triples correctly.[10]

Hits@K

Larger values mean better predictive performances.[10]

Mean rank (MR)

Mean rank is the average ranking position of the items predicted by the model among all the possible items.[10]

The smaller the value, the better the model.[10]

Mean reciprocal rank (MRR)

Mean reciprocal rank measures the number of triples predicted correctly.[10] If the first predicted triple is correct, then 1 is added, if the second is correct is summed, and so on.[10]

Mean reciprocal rank is generally used to quantify the effect of search algorithms.[10]

The larger the index, the better the model.[10]

Applications

Machine learning tasks

Knowledge graph completion (KGC) is a collection of techniques to infer knowledge from an embedded knowledge graph representation.[11] In particular, this technique completes a triple inferring the missing entity or relation.[11] The corresponding sub-tasks are named link or entity prediction (i.e., guessing an entity from the embedding given the other entity of the triple and the relation), and relation prediction (i.e., forecasting the most plausible relation that connects two entities).[11]

Triple Classification is a binary classification problem.[1] Given a triple, the trained model evaluates the plausibility of the triple using the embedding to determine if a triple is true or false.[11] The decision is made with the model score function and a given threshold.[11] Clustering is another application that leverages the embedded representation of a sparse knowledge graph to condense the representation of similar semantic entities close in a 2D space.[4]

Real world applications

The use of knowledge graph embedding is increasingly pervasive in many applications. In the case of recommender systems, the use of knowledge graph embedding can overcome the limitations of the usual reinforcement learning.[12][13] Training this kind of recommender system requires a huge amount of information from the users; however, knowledge graph techniques can address this issue by using a graph already constructed over a prior knowledge of the item correlation and using the embedding to infer from it the recommendation.[12] Drug repurposing is the use of an already approved drug, but for a therapeutic purpose different from the one for which it was initially designed.[14] It is possible to use the task of link prediction to infer a new connection between an already existing drug and a disease by using a biomedical knowledge graph built leveraging the availability of massive literature and biomedical databases.[14] Knowledge graph embedding can also be used in the domain of social politics.[4]

Models

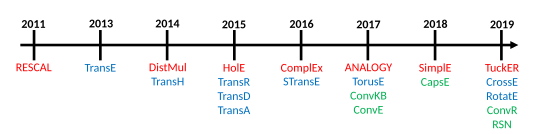
Publication timeline of some knowledge graph embedding models. In red the tensor decomposition models, in blue the geometric models, and in green the deep learning models. RESCAL[15] (2011) was the first modern KGE approach. In[16] it was applied to the YAGO knowledge graph. This was the first application of KGE to a large scale knowledge graph.

Given a collection of triples (or facts) , the knowledge graph embedding model produces, for each entity and relation present in the knowledge graph a continuous vector representation.[7] is the corresponding embedding of a triple with and , where is the embedding dimension for the entities, and for the relations.[7] The score function of a given model is denoted by and measures the distance of the embedding of the head from the embedding of tail given the embedding of the relation, or in other words, it quantifies the plausibility of the embedded representation of a given fact.[5]

Rossi et al. propose a taxonomy of the embedding models and identifies three main families of models: tensor decomposition models, geometric models, and deep learning models.[5]

Tensor decomposition model

The tensor decomposition is a family of knowledge graph embedding models that use a multi-dimensional matrix to represent a knowledge graph,[1][5][17] that is partially knowable due to the gaps of the knowledge graph describing a particular domain thoroughly.[5] In particular, these models use a three-way (3D) tensor, which is then factorized into low-dimensional vectors that are the entities and relations embeddings.[5][17] The third-order tensor is a suitable methodology to represent a knowledge graph because it records only the existence or the absence of a relation between entities,[17] and for this reason is simple, and there is no need to know a priori the network structure,[15] making this class of embedding models light, and easy to train even if they suffer from high-dimensional and sparsity of data.[5][17]

Bilinear models

This family of models uses a linear equation to embed the connection between the entities through a relation.[1] In particular, the embedded representation of the relations is a bidimensional matrix.[5] These models, during the embedding procedure, only use the single facts to compute the embedded representation and ignore the other associations to the same entity or relation.[18]

  • DistMult[19]: Since the embedding matrix of the relation is a diagonal matrix,[5] the scoring function can not distinguish asymmetric facts.[5][18]
  • ComplEx[20]: As DistMult uses a diagonal matrix to represent the relations embedding but adds a representation in the complex vector space and the hermitian product, it can distinguish symmetric and asymmetric facts.[5][17] This approach is scalable to a large knowledge graph in terms of time and space cost.[20]
  • ANALOGY[21]: This model encodes in the embedding the analogical structure of the knowledge graph to simulate inductive reasoning.[21][5][1] Using a differentiable objective function, ANALOGY has good theoretical generality and computational scalability.[21] It is proven that the embedding produced by ANALOGY fully recovers the embedding of DistMult, ComplEx, and HolE.[21]
  • SimplE[22]: This model is the improvement of canonical polyadic decomposition (CP), in which an embedding vector for the relation and two independent embedding vectors for each entity are learned, depending on whether it is a head or a tail in the knowledge graph fact.[22] SimplE resolves the problem of independent learning of the two entity embeddings using an inverse relation and average the CP score of and .[7][17] In this way, SimplE collects the relation between entities while they appear in the role of subject or object inside a fact, and it is able to embed asymmetric relations.[5]

Non-bilinear models

  • HolE:[23] HolE uses circular correlation to create an embedded representation of the knowledge graph,[23] which can be seen as a compression of the matrix product, but is more computationally efficient and scalable while keeping the capabilities to express asymmetric relation since the circular correlation is not commutative.[18] HolE links holographic and complex embeddings since, if used together with Fourier, can be seen as a special case of ComplEx.[1]
  • TuckER:[24] TuckER sees the knowledge graph as a tensor that could be decomposed using the Tucker decomposition in a collection of vectors—i.e., the embeddings of entities and relations—with a shared core.[24][5] The weights of the core tensor are learned together with the embeddings and represent the level of interaction of the entries.[25] Each entity and relation has its own embedding dimension, and the size of the core tensor is determined by the shape of the entities and relations that interact.[5] The embedding of the subject and object of a fact are summed in the same way, making TuckER fully expressive, and other embedding models such as RESCAL, DistMult, ComplEx, and SimplE can be expressed as a special formulation of TuckER.[24]
  • MEI:[26] MEI introduces the multi-partition embedding interaction technique with the block term tensor format, which is a generalization of CP decomposition and Tucker decomposition. It divides the embedding vector into multiple partitions and learns the local interaction patterns from data instead of using fixed special patterns as in ComplEx or SimplE models. This enables MEI to achieve optimal efficiency—expressiveness trade-off, not just being fully expressive.[26] Previous models such as TuckER, RESCAL, DistMult, ComplEx, and SimplE are suboptimal restricted special cases of MEI.
  • MEIM:[27] MEIM goes beyond the block term tensor format to introduce the independent core tensor for ensemble boosting effects and the soft orthogonality for max-rank relational mapping, in addition to multi-partition embedding interaction. MEIM generalizes several previous models such as MEI and its subsumed models, RotaE, and QuatE.[27] MEIM improves expressiveness while still being highly efficient in practice, helping it achieve good results using fairly small model sizes.

Geometric models

The geometric space defined by this family of models encodes the relation as a geometric transformation between the head and tail of a fact.[5] For this reason, to compute the embedding of the tail, it is necessary to apply a transformation to the head embedding, and a distance function is used to measure the goodness of the embedding or to score the reliability of a fact.[5]

Geometric models are similar to the tensor decomposition model, but the main difference between the two is that they have to preserve the applicability of the transformation in the geometric space in which it is defined.[5]

Pure translational models

This class of models is inspired by the idea of translation invariance introduced in word2vec.[7] A pure translational model relies on the fact that the embedding vector of the entities are close to each other after applying a proper relational translation in the geometric space in which they are defined.[18] In other words, given a fact, when the embedding of head is added to the embedding of relation, the expected result should be the embedding of the tail.[5] The closeness of the entities embedding is given by some distance measure and quantifies the reliability of a fact.[17]

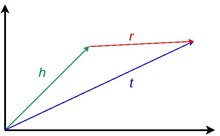
TransE embedding model. The vector representation (embedding) of the head plus the vector representation of the relation should be equal to the vector representation of the tail entity.
  • TransE[9]: This model uses a scoring function that forces the embeddings to satisfy a simple vector sum equation in each fact in which they appear: .[7] The embedding will be exact if each entity and relation appears in only one fact, and, for this reason, in practice does not well represent one-to-many, many-to-one, and asymmetric relations.[5][7]
  • TransH[28]: It is an evolution of TransE introducing a hyperplane as geometric space to solve the problem of representing correctly the types of relations.[28] In TransH, each relation has a different embedded representation, on a different hyperplane, based on which entities it interacts with.[7] Therefore, to compute, for example, the score function of a fact, the embedded representation of the head and tail need to be projected using a relational projection matrix on the correct hyperplane of the relation.[1][7]
  • TransR[29]: TransR is an evolution of TransH because it uses two different spaces to represent the embedded representation of the entities and the relations,[1][18] and separate completely the semantic space of entities and relations.[7] Also TransR uses a relational projection matrix to translate the embedding of the entities to the relation space.[7]
  • TransD:[30] Given a fact, in TransR, the head and the tail of a fact could belongs to two different types of entities, for example, in the fact, Obama and USA are two entities but one is a person and the other is a country.[30][7] The matrix multiplication also is an expensive procedure in TransR to compute the projection.[7][30] In this context, TransD employs two vector for each entity-relation pair to compute a dynamic mapping that substitutes the projection matrix while reducing the dimensional complexity.[1][7][30] The first vector is used to represent the semantic meaning of the entities and relations, the second one to compute the mapping matrix.[30]
  • TransA:[31] All the translational models define a score function in their representation space, but they oversimplify this metric loss.[31] Since the vector representation of the entities and relations is not perfect, a pure translation of could be distant from , and a spherical equipotential Euclidean distance makes it hard to distinguish which is the closest entity.[31] TransA, instead, introduces an adaptive Mahalanobis distance to weights the embedding dimensions, together with elliptical surfaces to remove the ambiguity.[1][7][31]

Translational models with additional embeddings

It is possible to associate additional information to each element in the knowledge graph and their common representation facts.[1] Each entity and relation can be enriched with text descriptions, weights, constraints, and others in order to improve the overall description of the domain with a knowledge graph.[1] During the embedding of the knowledge graph, this information can be used to learn specialized embeddings for these characteristics together with the usual embedded representation of entities and relations, with the cost of learning a more significant number of vectors.[5]

  • STransE:[32] This model is the result of the combination of TransE and of the structure embedding[32] in such a way it is able to better represent the one-to-many, many-to-one, and many-to-many relations.[5] To do so, the model involves two additional independent matrix and for each embedded relation in the KG.[32] Each additional matrix is used based on the fact the specific relation interact with the head or the tail of the fact.[32] In other words, given a fact , before applying the vector translation, the head is multiplied by and the tail is multiplied by .[7]
  • CrossE:[33] Crossover interactions can be used for related information selection, and could be very useful for the embedding procedure.[33] Crossover interactions provide two distinct contributions in the information selection: interactions from relations to entities and interactions from entities to relations.[33] This means that a relation, e.g.'president_of' automatically selects the types of entities that are connecting the subject to the object of a fact.[33] In a similar way, the entity of a fact inderectly determine which is inference path that has to be choose to predict the object of a related triple.[33] CrossE, to do so, learns an additional interaction matrix , uses the element-wise product to compute the interaction between and .[5][33] Even if, CrossE, does not rely on a neural network architecture, it is shown that this methodology can be encoded in such architecture.[1]

Roto-translational models

This family of models, in addition or in substitution of a translation they employ a rotation-like transformation.[5]

  • TorusE:[34] The regularization term of TransE makes the entity embedding to build a spheric space, and consequently loses the translation properties of the geometric space.[34] To address this problem, TorusE leverages the use of a compact Lie group that in this specific case is n-dimensional torus space, and avoid the use of regularization.[1][34] TorusE defines the distance functions to substitute the L1 and L2 norm of TransE.[5]
  • RotatE:[35] RotatE is inspired by the Euler's identity and involves the use of Hadamard product to represent a relation as a rotation from the head to the tail in the complex space.[35] For each element of the triple, the complex part of the embedding describes a counterclockwise rotation respect to an axis, that can be describe with the Euler's identity, whereas the modulus of the relation vector is 1.[35] It is shown that the model is capable of embedding symmetric, asymmetric, inversion, and composition relations from the knowledge graph.[35]

Deep learning models

This group of embedding models uses deep neural network to learn patterns from the knowledge graph that are the input data.[5] These models have the generality to distinguish the type of entity and relation, temporal information, path information, underlay structured information,[18] and resolve the limitations of distance-based and semantic-matching-based models in representing all the features of a knowledge graph.[1] The use of deep learning for knowledge graph embedding has shown good predictive performance even if they are more expensive in the training phase, data-hungry, and often required a pre-trained embedding representation of knowledge graph coming from a different embedding model.[1][5]

Convolutional neural networks

This family of models, instead of using fully connected layers, employs one or more convolutional layers that convolve the input data applying a low-dimensional filter capable of embedding complex structures with few parameters by learning nonlinear features.[1][5][18]

  • ConvE:[36] ConvE is an embedding model that represents a good tradeoff expressiveness of deep learning models and computational expensiveness,[17] in fact it is shown that it used 8x less parameters, when compared to DistMult.[36] ConvE uses a one-dimensional -sized embedding to represent the entities and relations of a knowledge graph.[5][36] To compute the score function of a triple, ConvE apply a simple procedure: first concatenes and merge the embeddings of the head of the triple and the relation in a single data , then this matrix is used as input for the 2D convolutional layer.[5][17] The result is then passed through a dense layer that apply a linear transformation parameterized by the matrix and at the end, with the inner product is linked to the tail triple.[5][18] ConvE is also particularly efficient in the evaluation procedure: using a 1-N scoring, the model matches, given a head and a relation, all the tails at the same time, saving a lot of evaluation time when compared to the 1-1 evaluation program of the other models.[18]
  • ConvR:[37] ConvR is an adaptive convolutional network aimed to deeply represent all the possible interactions between the entities and the relations.[37] For this task, ConvR, computes convolutional filter for each relation, and, when required, applies these filters to the entity of interest to extract convoluted features.[37] The procedure to compute the score of triple is the same as ConvE.[5]
  • ConvKB:[38] ConvKB, to compute score function of a given triple , it produces an input of dimension without reshaping and passes it to series of convolutional filter of size .[38] This result feeds a dense layer with only one neuron that produces the final score.[38] The single final neuron makes this architecture as a binary classifier in which the fact could be true or false.[5] A difference with ConvE is that the dimensionality of the entities is not changed.[17]

Capsule neural networks

This family of models uses capsule neural networks to create a more stable representation that is able to recognize a feature in the input without losing spatial information.[5] The network is composed of convolutional layers, but they are organized in capsules, and the overall result of a capsule is sent to a higher-capsule decided by a dynamic process routine.[5]

  • CapsE:[39] CapsE implements a capsule network to model a fact .[39] As in ConvKB, each triple element is concatenated to build a matrix and is used to feed to a convolutional layer to extract the convolutional features.[5][39] These features are then redirected to a capsule to produce a continuous vector, more the vector is long, more the fact is true.[39]

Recurrent neural networks

This class of models leverages the use of recurrent neural network.[5] The advantage of this architecture is to memorize a sequence of fact, rather than just elaborate single events.[40]

  • RSN:[40] During the embedding procedure is commonly assumed that, similar entities has similar relations.[40] In practice, this type of information is not leveraged, because the embedding is computed just on the undergoing fact rather than a history of facts.[40] Recurrent skipping networks (RSN) uses a recurrent neural network to learn relational path using a random walk sampling.[5][40]

Model performance

The machine learning task for knowledge graph embedding that is more often used to evaluate the embedding accuracy of the models is the link prediction.[1][3][5][6][7][18] Rossi et al.[5] produced an extensive benchmark of the models, but also other surveys produces similar results.[3][7][18][25] The benchmark involves five datasets FB15k,[9] WN18,[9] FB15k-237,[41] WN18RR,[36] and YAGO3-10.[42] More recently, it has been discussed that these datasets are far away from real-world applications, and other datasets should be integrated as a standard benchmark.[43]

Table summary of the characteristics of the datasets used to benchmark the embedding models.
Dataset name Number of different entities Number of different relations Number of triples
FB15k[9] 14951 1345 584,113
WN18[9] 40943 18 151,442
FB15k-237[41] 14541 237 310,116
WN18RR[36] 40943 11 93,003
YAGO3-10[42] 123182 37 1,089,040
Table summary of the memory complexity and the link prediction accuracy of the knowledge graph embedding models according to Rossi et al.[5] in terms of Hits@10, MR, and MRR. Best results on each metric for each dataset are in bold.
Model name Memory complexity FB15K (Hits@10) FB15K (MR) FB15K (MRR) FB15K - 237 (Hits@10) FB15K - 237 (MR) FB15K - 237 (MRR) WN18 (Hits@10) WN18 (MR) WN18 (MRR) WN18RR (Hits@10) WN18RR (MR) WN18RR (MRR) YAGO3-10 (Hits@10) YAGO3-10 (MR) YAGO3-10 (MRR)
DistMul[19] 0.863 173 0.784 0.490 199 0.313 0.946 675 0.824 0.502 5913 0.433 0.661 1107 0.501
ComplEx[20] 0.905 34 0.848 0.529 202 0.349 0.955 3623 0.949 0.521 4907 0.458 0.703 1112 0.576
HolE[23] 0.867 211 0.800 0.476 186 0.303 0.949 650 0.938 0.487 8401 0.432 0.651 6489 0.502
ANALOGY[21] 0.837 126 0.726 0.353 476 0.202 0.944 808 0.934 0.380 9266 0.366 0.456 2423 0.283
SimplE[22] 0.836 138 0.726 0.343 651 0.179 0.945 759 0.938 0.426 8764 0.398 0.631 2849 0.453
TuckER[24] 0.888 39 0.788 0.536 162 0.352 0.958 510 0.951 0.514 6239 0.459 0.680 2417 0.544
MEI[26] 0.552 145 0.365 0.551 3268 0.481 0.709 756 0.578
MEIM[27] 0.557 137 0.369 0.577 2434 0.499 0.716 747 0.585
TransE[9] 0.847 45 0.628 0.497 209 0.310 0.948 279 0.646 0.495 3936 0.206 0.673 1187 0.501
STransE[32] 0.796 69 0.543 0.495 357 0.315 0.934 208 0.656 0.422 5172 0.226 0.073 5797 0.049
CrossE[33] 0.862 136 0.702 0.470 227 0.298 0.950 441 0.834 0.449 5212 0.405 0.654 3839 0.446
TorusE[34] 0.839 143 0.746 0.447 211 0.281 0.954 525 0.947 0.535 4873 0.463 0.474 19455 0.342
RotatE[35] 0.881 42 0.791 0.522 178 0.336 0.960 274 0.949 0.573 3318 0.475 0.570 1827 0.498
ConvE[36] 0.849 51 0.688 0.521 281 0.305 0.956 413 0.945 0.507 4944 0.427 0.657 2429 0.488
ConvKB[38] 0.408 324 0.211 0.517 309 0.230 0.948 202 0.709 0.525 3429 0.249 0.604 1683 0.420
ConvR[37] 0.885 70 0.773 0.526 251 0.346 0.958 471 0.950 0.526 5646 0.467 0.673 2582 0.527
CapsE[39] 0.217 610 0.087 0.356 405 0.160 0.950 233 0.890 0.559 720 0.415 0 60676 0.000
RSN[40] 0.870 51 0.777 0.444 248 0.280 0.951 346 0.928 0.483 4210 0.395 0.664 1339 0.511

Libraries

See also

References

  1. ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa Ji, Shaoxiong; Pan, Shirui; Cambria, Erik; Marttinen, Pekka; Yu, Philip S. (2021). "A Survey on Knowledge Graphs: Representation, Acquisition, and Applications". IEEE Transactions on Neural Networks and Learning Systems. PP (2): 494–514. arXiv:2002.00388. doi:10.1109/TNNLS.2021.3070843. hdl:10072/416709. ISSN 2162-237X. PMID 33900922. S2CID 211010433.
  2. ^ Mohamed, Sameh K; Nováček, Vít; Nounu, Aayah (2019-08-01). Cowen, Lenore (ed.). "Discovering Protein Drug Targets Using Knowledge Graph Embeddings". Bioinformatics. 36 (2): 603–610. doi:10.1093/bioinformatics/btz600. hdl:10379/15375. ISSN 1367-4803. PMID 31368482.
  3. ^ a b c d Lin, Yankai; Han, Xu; Xie, Ruobing; Liu, Zhiyuan; Sun, Maosong (2018-12-28). "Knowledge Representation Learning: A Quantitative Review". arXiv:1812.10901 [cs.CL].
  4. ^ a b c Abu-Salih, Bilal; Al-Tawil, Marwan; Aljarah, Ibrahim; Faris, Hossam; Wongthongtham, Pornpit; Chan, Kit Yan; Beheshti, Amin (2021-05-12). "Relational Learning Analysis of Social Politics using Knowledge Graph Embedding". Data Mining and Knowledge Discovery. 35 (4): 1497–1536. arXiv:2006.01626. doi:10.1007/s10618-021-00760-w. ISSN 1573-756X. S2CID 219179556.
  5. ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai aj ak al am an ao ap aq ar as Rossi, Andrea; Barbosa, Denilson; Firmani, Donatella; Matinata, Antonio; Merialdo, Paolo (2020). "Knowledge Graph Embedding for Link Prediction: A Comparative Analysis". ACM Transactions on Knowledge Discovery from Data. 15 (2): 1–49. arXiv:2002.00819. doi:10.1145/3424672. hdl:11573/1638610. ISSN 1556-4681. S2CID 211011226.
  6. ^ a b Paulheim, Heiko (2016-12-06). Cimiano, Philipp (ed.). "Knowledge graph refinement: A survey of approaches and evaluation methods". Semantic Web. 8 (3): 489–508. doi:10.3233/SW-160218. S2CID 13151033.
  7. ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab Dai, Yuanfei; Wang, Shiping; Xiong, Neal N.; Guo, Wenzhong (May 2020). "A Survey on Knowledge Graph Embedding: Approaches, Applications and Benchmarks". Electronics. 9 (5): 750. doi:10.3390/electronics9050750.
  8. ^ Guo, Shu; Wang, Quan; Wang, Bin; Wang, Lihong; Guo, Li (2015). "Semantically Smooth Knowledge Graph Embedding". Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers). Association for Computational Linguistics. pp. 84–94. doi:10.3115/v1/P15-1009. S2CID 205692.
  9. ^ a b c d e f g Bordes, Antoine; Usunier, Nicolas; Garcia-Durán, Alberto; Weston, Jason; Yakhnenko, Oksana (May 2013). "Translating embeddings for modeling multi-relational data". NIPS'13: Proceedings of the 26th International Conference on Neural Information Processing Systems. Curran Associates Inc. pp. 2787–2795.
  10. ^ a b c d e f g h i j k l Chen, Zhe; Wang, Yuehan; Zhao, Bin; Cheng, Jing; Zhao, Xin; Duan, Zongtao (2020). "Knowledge Graph Completion: A Review". IEEE Access. 8: 192435–192456. Bibcode:2020IEEEA...8s2435C. doi:10.1109/ACCESS.2020.3030076. ISSN 2169-3536. S2CID 226230006.
  11. ^ a b c d e Cai, Hongyun; Zheng, Vincent W.; Chang, Kevin Chen-Chuan (2018-02-02). "A Comprehensive Survey of Graph Embedding: Problems, Techniques and Applications". arXiv:1709.07604 [cs.AI].
  12. ^ a b Zhou, Sijin; Dai, Xinyi; Chen, Haokun; Zhang, Weinan; Ren, Kan; Tang, Ruiming; He, Xiuqiang; Yu, Yong (2020-06-18). "Interactive Recommender System via Knowledge Graph-enhanced Reinforcement Learning". arXiv:2006.10389 [cs.IR].
  13. ^ Liu, Chan; Li, Lun; Yao, Xiaolu; Tang, Lin (August 2019). "A Survey of Recommendation Algorithms Based on Knowledge Graph Embedding". 2019 IEEE International Conference on Computer Science and Educational Informatization (CSEI). pp. 168–171. doi:10.1109/CSEI47661.2019.8938875. ISBN 978-1-7281-2308-0. S2CID 209459928.
  14. ^ a b Sosa, Daniel N.; Derry, Alexander; Guo, Margaret; Wei, Eric; Brinton, Connor; Altman, Russ B. (2020). "A Literature-Based Knowledge Graph Embedding Method for Identifying Drug Repurposing Opportunities in Rare Diseases". Pacific Symposium on Biocomputing. Pacific Symposium on Biocomputing. 25: 463–474. ISSN 2335-6936. PMC 6937428. PMID 31797619.
  15. ^ a b Nickel, Maximilian; Tresp, Volker; Kriegel, Hans-Peter (2011-06-28). "A three-way model for collective learning on multi-relational data". ICML'11: Proceedings of the 28th International Conference on International Conference on Machine Learning. Omnipress. pp. 809–816. ISBN 978-1-4503-0619-5.
  16. ^ Nickel, Maximilian; Tresp, Volker; Kriegel, Hans-Peter (2012-04-16). "Factorizing YAGO". Proceedings of the 21st international conference on World Wide Web. Association for Computing Machinery. pp. 271–280. doi:10.1145/2187836.2187874. ISBN 978-1-4503-1229-5. S2CID 6348464.
  17. ^ a b c d e f g h i j Alshahrani, Mona; Thafar, Maha A.; Essack, Magbubah (2021-02-18). "Application and evaluation of knowledge graph embeddings in biomedical data". PeerJ Computer Science. 7: e341. doi:10.7717/peerj-cs.341. ISSN 2376-5992. PMC 7959619. PMID 33816992.
  18. ^ a b c d e f g h i j k Wang, Meihong; Qiu, Linling; Wang, Xiaoli (2021-03-16). "A Survey on Knowledge Graph Embeddings for Link Prediction". Symmetry. 13 (3): 485. Bibcode:2021Symm...13..485W. doi:10.3390/sym13030485. ISSN 2073-8994.
  19. ^ a b Yang, Bishan; Yih, Wen-tau; He, Xiaodong; Gao, Jianfeng; Deng, Li (2015-08-29). "Embedding Entities and Relations for Learning and Inference in Knowledge Bases". arXiv:1412.6575 [cs.CL].
  20. ^ a b c Trouillon, Théo; Welbl, Johannes; Riedel, Sebastian; Gaussier, Éric; Bouchard, Guillaume (2016-06-20). "Complex Embeddings for Simple Link Prediction". arXiv:1606.06357 [cs.AI].
  21. ^ a b c d e Liu, Hanxiao; Wu, Yuexin; Yang, Yiming (2017-07-06). "Analogical Inference for Multi-Relational Embeddings". arXiv:1705.02426 [cs.LG].
  22. ^ a b c Kazemi, Seyed Mehran; Poole, David (2018-10-25). "SimplE Embedding for Link Prediction in Knowledge Graphs". arXiv:1802.04868 [stat.ML].
  23. ^ a b c Nickel, Maximilian; Rosasco, Lorenzo; Poggio, Tomaso (2015-12-07). "Holographic Embeddings of Knowledge Graphs". arXiv:1510.04935 [cs.AI].
  24. ^ a b c d Balažević, Ivana; Allen, Carl; Hospedales, Timothy M. (2019). "TuckER: Tensor Factorization for Knowledge Graph Completion". Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP). pp. 5184–5193. arXiv:1901.09590. doi:10.18653/v1/D19-1522. S2CID 59316623.
  25. ^ a b Ali, Mehdi; Berrendorf, Max; Hoyt, Charles Tapley; Vermue, Laurent; Galkin, Mikhail; Sharifzadeh, Sahand; Fischer, Asja; Tresp, Volker; Lehmann, Jens (2021). "Bringing Light into the Dark: A Large-scale Evaluation of Knowledge Graph Embedding Models under a Unified Framework". IEEE Transactions on Pattern Analysis and Machine Intelligence. PP (12): 8825–8845. arXiv:2006.13365. doi:10.1109/TPAMI.2021.3124805. PMID 34735335. S2CID 220041612.
  26. ^ a b c Tran, Hung Nghiep; Takasu, Atsuhiro (2020). "Multi-Partition Embedding Interaction with Block Term Format for Knowledge Graph Completion". Proceedings of the European Conference on Artificial Intelligence (ECAI 2020). Frontiers in Artificial Intelligence and Applications. Vol. 325. IOS Press. pp. 833–840. doi:10.3233/FAIA200173. S2CID 220265751.
  27. ^ a b c Tran, Hung-Nghiep; Takasu, Atsuhiro (2022-07-16). "MEIM: Multi-partition Embedding Interaction Beyond Block Term Format for Efficient and Expressive Link Prediction". Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence. Vol. 3. pp. 2262–2269. doi:10.24963/ijcai.2022/314. ISBN 978-1-956792-00-3. S2CID 250635995.
  28. ^ a b Wang, Zhen (2014). "Knowledge Graph Embedding by Translating on Hyperplanes". Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 28. doi:10.1609/aaai.v28i1.8870. S2CID 15027084.
  29. ^ Lin, Yankai; Liu, Zhiyuan; Sun, Maosong; Liu, Yang; Zhu, Xuan (2015-01-25). Learning entity and relation embeddings for knowledge graph completion. AAAI Press. pp. 2181–2187. ISBN 978-0-262-51129-2.
  30. ^ a b c d e Ji, Guoliang; He, Shizhu; Xu, Liheng; Liu, Kang; Zhao, Jun (July 2015). "Knowledge Graph Embedding via Dynamic Mapping Matrix". Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers). Association for Computational Linguistics. pp. 687–696. doi:10.3115/v1/P15-1067. S2CID 11202498.
  31. ^ a b c d Xiao, Han; Huang, Minlie; Hao, Yu; Zhu, Xiaoyan (2015-09-27). "TransA: An Adaptive Approach for Knowledge Graph Embedding". arXiv:1509.05490 [cs.CL].
  32. ^ a b c d e Nguyen, Dat Quoc; Sirts, Kairit; Qu, Lizhen; Johnson, Mark (June 2016). "STransE: A novel embedding model of entities and relationships in knowledge bases". Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. Association for Computational Linguistics. pp. 460–466. arXiv:1606.08140. doi:10.18653/v1/N16-1054. S2CID 9884935.
  33. ^ a b c d e f g Zhang, Wen; Paudel, Bibek; Zhang, Wei; Bernstein, Abraham; Chen, Huajun (2019-01-30). "Interaction Embeddings for Prediction and Explanation in Knowledge Graphs". Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining. pp. 96–104. arXiv:1903.04750. doi:10.1145/3289600.3291014. ISBN 9781450359405. S2CID 59516071.
  34. ^ a b c d Ebisu, Takuma; Ichise, Ryutaro (2017-11-15). "TorusE: Knowledge Graph Embedding on a Lie Group". arXiv:1711.05435 [cs.AI].
  35. ^ a b c d e Sun, Zhiqing; Deng, Zhi-Hong; Nie, Jian-Yun; Tang, Jian (2019-02-26). "RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space". arXiv:1902.10197 [cs.LG].
  36. ^ a b c d e f Dettmers, Tim; Minervini, Pasquale; Stenetorp, Pontus; Riedel, Sebastian (2018-07-04). "Convolutional 2D Knowledge Graph Embeddings". arXiv:1707.01476 [cs.LG].
  37. ^ a b c d Jiang, Xiaotian; Wang, Quan; Wang, Bin (June 2019). "Adaptive Convolution for Multi-Relational Learning". Proceedings of the 2019 Conference of the North. Association for Computational Linguistics. pp. 978–987. doi:10.18653/v1/N19-1103. S2CID 174800352.
  38. ^ a b c d Nguyen, Dai Quoc; Nguyen, Tu Dinh; Nguyen, Dat Quoc; Phung, Dinh (2018). "A Novel Embedding Model for Knowledge Base Completion Based on Convolutional Neural Network". Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 2 (Short Papers). pp. 327–333. arXiv:1712.02121. doi:10.18653/v1/N18-2053. S2CID 3882054.
  39. ^ a b c d e Nguyen, Dai Quoc; Vu, Thanh; Nguyen, Tu Dinh; Nguyen, Dat Quoc; Phung, Dinh (2019-03-06). "A Capsule Network-based Embedding Model for Knowledge Graph Completion and Search Personalization". arXiv:1808.04122 [cs.CL].
  40. ^ a b c d e f Guo, Lingbing; Sun, Zequn; Hu, Wei (2019-05-13). "Learning to Exploit Long-term Relational Dependencies in Knowledge Graphs". arXiv:1905.04914 [cs.AI].
  41. ^ a b Toutanova, Kristina; Chen, Danqi (July 2015). "Observed versus latent features for knowledge base and text inference". Proceedings of the 3rd Workshop on Continuous Vector Space Models and their Compositionality. Association for Computational Linguistics. pp. 57–66. doi:10.18653/v1/W15-4007. S2CID 5378837.
  42. ^ a b Mahdisoltani, F.; Biega, J.; Suchanek, Fabian M. (2015). "YAGO3: A Knowledge Base from Multilingual Wikipedias". CIDR. S2CID 6611164.
  43. ^ Hu, Weihua; Fey, Matthias; Zitnik, Marinka; Dong, Yuxiao; Ren, Hongyu; Liu, Bowen; Catasta, Michele; Leskovec, Jure (2021-02-24). "Open Graph Benchmark: Datasets for Machine Learning on Graphs". arXiv:2005.00687 [cs.LG].
Scholia has a topic profile for Knowledge graph embedding.
Quelle: http://en.wikipedia.org/wiki/Knowledge_graph_embedding