Nakagami distribution
Probability density function 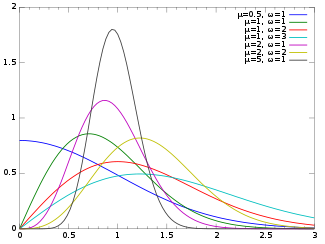 | |||
Cumulative distribution function 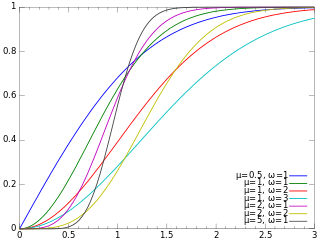 | |||
| Parameters |
shape (real) scale (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | |||
| Median | No simple closed form | ||
| Mode | |||
| Variance | |||
The Nakagami distribution or the Nakagami-m distribution is a probability distribution related to the gamma distribution. The family of Nakagami distributions has two parameters: a shape parameter and a scale parameter . It is used to model physical phenomena such as those found in medical ultrasound imaging, communications engineering, meteorology, hydrology, multimedia, and seismology.
Characterization
Its probability density function (pdf) is[1]
where and .
Its cumulative distribution function (CDF) is[1]
where P is the regularized (lower) incomplete gamma function.
Parameterization
The parameters and are[2]
and
No closed form solution exists for the median of this distribution, although special cases do exist, such as when m = 1. For practical purposes the median would have to be calculated as the 50th-percentile of the observations.
Parameter estimation
An alternative way of fitting the distribution is to re-parametrize as σ = Ω/m.[3]
Given independent observations from the Nakagami distribution, the likelihood function is
Its logarithm is
Therefore
These derivatives vanish only when
and the value of m for which the derivative with respect to m vanishes is found by numerical methods including the Newton–Raphson method.
It can be shown that at the critical point a global maximum is attained, so the critical point is the maximum-likelihood estimate of (m,σ). Because of the equivariance of maximum-likelihood estimation, a maximum likelihood estimate for Ω is obtained as well.
Random variate generation
The Nakagami distribution is related to the gamma distribution. In particular, given a random variable , it is possible to obtain a random variable , by setting , , and taking the square root of :
Alternatively, the Nakagami distribution can be generated from the chi distribution with parameter set to and then following it by a scaling transformation of random variables. That is, a Nakagami random variable is generated by a simple scaling transformation on a chi-distributed random variable as below.
For a chi-distribution, the degrees of freedom must be an integer, but for Nakagami the can be any real number greater than 1/2. This is the critical difference and accordingly, Nakagami-m is viewed as a generalization of chi-distribution, similar to a gamma distribution being considered as a generalization of chi-squared distributions.
History and applications
The Nakagami distribution is relatively new, being first proposed in 1960 by Minoru Nakagami as a mathematical model for small-scale fading in long-distance high-frequency radio wave propagation.[4] It has been used to model attenuation of wireless signals traversing multiple paths[5] and to study the impact of fading channels on wireless communications.[6]
Related distributions
- Restricting m to the unit interval (q = m; 0 < q < 1)[dubious – discuss] defines the Nakagami-q distribution, also known as Hoyt distribution, first studied by R.S. Hoyt in the 1940s.[7][8][9] In particular, the radius around the true mean in a bivariate normal random variable, re-written in polar coordinates (radius and angle), follows a Hoyt distribution. Equivalently, the modulus of a complex normal random variable also does.
- With 2m = k, the Nakagami distribution gives a scaled chi distribution.
- With , the Nakagami distribution gives a scaled half-normal distribution.
- A Nakagami distribution is a particular form of generalized gamma distribution, with p = 2 and d = 2m.
See also
References
- ^ a b Laurenson, Dave (1994). "Nakagami Distribution". Indoor Radio Channel Propagation Modelling by Ray Tracing Techniques. Retrieved 2007-08-04.
- ^ R. Kolar, R. Jirik, J. Jan (2004) "Estimator Comparison of the Nakagami-m Parameter and Its Application in Echocardiography", Radioengineering, 13 (1), 8–12
- ^ Mitra, Rangeet; Mishra, Amit Kumar; Choubisa, Tarun (2012). "Maximum Likelihood Estimate of Parameters of Nakagami-m Distribution". International Conference on Communications, Devices and Intelligent Systems (CODIS), 2012: 9–12.
- ^ Nakagami, M. (1960) "The m-Distribution, a general formula of intensity of rapid fading". In William C. Hoffman, editor, Statistical Methods in Radio Wave Propagation: Proceedings of a Symposium held June 18–20, 1958, pp. 3–36. Pergamon Press., doi:10.1016/B978-0-08-009306-2.50005-4
- ^ Parsons, J. D. (1992) The Mobile Radio Propagation Channel. New York: Wiley.
- ^ Ramon Sanchez-Iborra; Maria-Dolores Cano; Joan Garcia-Haro (2013). "Performance evaluation of QoE in VoIP traffic under fading channels". 2013 World Congress on Computer and Information Technology (WCCIT). pp. 1–6. doi:10.1109/WCCIT.2013.6618721. ISBN 978-1-4799-0462-4. S2CID 16810288.
- ^ Paris, J.F. (2009). "Nakagami-q (Hoyt) distribution function with applications". Electronics Letters. 45 (4): 210–211. Bibcode:2009ElL....45..210P. doi:10.1049/el:20093427.
- ^ "HoytDistribution".
- ^ "NakagamiDistribution".















![{\displaystyle m={\frac {\left(\operatorname {E} [X^{2}]\right)^{2}}{\operatorname {Var} [X^{2}]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e89f6d3915ba9cf5c8c0a65f2e7cf9ffca09438)
![{\displaystyle \Omega =\operatorname {E} [X^{2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5333b619dfc07cf7011c936ddaaf4290d6e94be6)


















