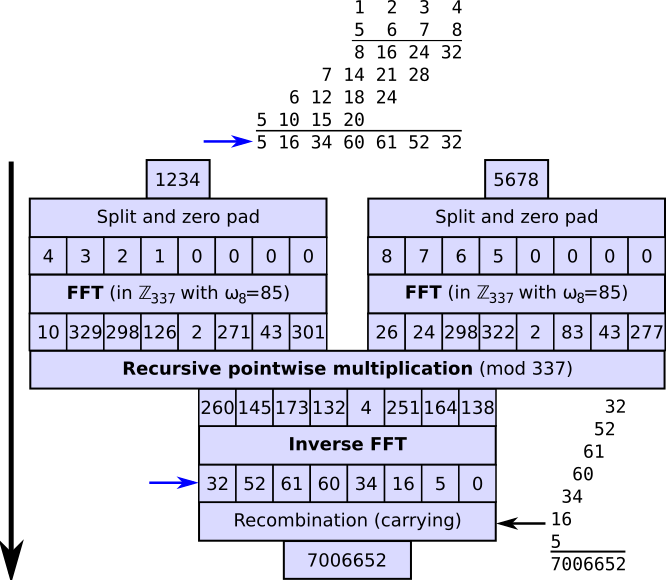
File:Integer multiplication by FFT.svg
Size of this PNG preview of this SVG file: 666 × 580 pixels. Other resolutions: 276 × 240 pixels | 551 × 480 pixels | 882 × 768 pixels | 1,176 × 1,024 pixels | 2,352 × 2,048 pixels.
Original file (SVG file, nominally 666 × 580 pixels, file size: 79 KB)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 10:37, 17 December 2011 |  | 666 × 580 (79 KB) | Dcoetzee |
File usage
The following 2 pages use this file:
Global file usage
The following other wikis use this file:
- Usage on de.wikipedia.org
- Usage on ja.wikipedia.org
- Usage on pl.wikipedia.org
- Usage on zh.wikipedia.org
