Davis's law
Davis's law is used in anatomy and physiology to describe how soft tissue models along imposed demands. It is similar to Wolff's law, which applies to osseous tissue. It is a physiological principle stating that soft tissue heal according to the manner in which they are mechanically stressed.[1]
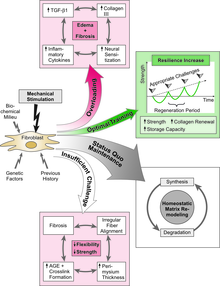
It is also an application of the Mechanostat model of Harold Frost which was originally developed to describe the adaptational response of bones; however – as outlined by Harold Frost himself – it also applies to fibrous collagenous connective tissues, such as ligaments, tendons and fascia.[2][3] The "stretch-hypertrophy rule" of that model states: "Intermittent stretch causes collagenous tissues to hypertrophy until the resulting increase in strength reduces elongation in tension to some minimum level".[4] Similar to the behavior of bony tissues this adaptational response occurs only if the mechanical strain exceeds a certain threshold value. Harold Frost proposed that for dense collagenous connective tissues the related threshold values are around 23 Newton/mm2 or 4% strain elongation.[5]
Origin
The term Davis's law is named after Henry Gassett Davis, an American orthopedic surgeon known for his work in developing traction methods. Its earliest known appearance is in John Joseph Nutt's 1913 book Diseases and Deformities of the Foot, where Nutt outlines the law by quoting a passage from Davis's 1867 book, Conservative Surgery:
- "Ligaments, or any soft tissue, when put under even a moderate degree of tension, if that tension is unremitting, will elongate by the addition of new material; on the contrary, when ligaments, or rather soft tissues, remain uninterruptedly in a loose or lax state, they will gradually shorten, as the effete material is removed, until they come to maintain the same relation to the bony structures with which they are united that they did before their shortening. Nature never wastes her time and material in maintaining a muscle or ligament at its original length when the distance between their points of origin and insertion is for any considerable time, without interruption, shortened."[6]
Davis's writing on the subject exposes a long chain of competing theories on the subject of soft tissue contracture and the causes of scoliosis. Davis's comments in Conservative Surgery were in the form of a sharp rebuke of lectures published by Louis Bauer of the Brooklyn Medical and Surgical Institute in 1862.[7] In his writing, Bauer claimed that "a contraction of ligaments is a physiological impossibility".[8] Bauer sided with work published in 1851 by Julius Konrad Werner, director of the Orthopedic Institute of Konigsberg, Prussia. Bauer and Werner, in turn, were contradicting research published by Jacques Mathieu Delpech in 1823.[9][10]
Soft tissue examples
Tendons are soft tissue structures that respond to changes in mechanical loading. Bulk mechanical properties, such as modulus, failure strain, and ultimate tensile strength, decrease over long periods of disuse as a result of micro-structural changes on the collagen fiber level. In micro-gravity simulations, human test subjects can experience gastrocnemius tendon strength loss of up to 58% over a 90-day period.[11] Test subjects who were allowed to engage in resistance training displayed a smaller magnitude of tendon strength loss in the same micro-gravity environment, but modulus strength decrease was still significant.
Conversely, tendons that have lost their original strength due to extended periods of inactivity can regain most of their mechanical properties through gradual re-loading of the tendon,[12] due to the tendon's response to mechanical loading. Biological signaling events initiate re-growth at the site, while mechanical stimuli further promote rebuilding. This 6-8 week process results in an increase of the tendon's mechanical properties until it recovers its original strength.[13] However, excessive loading during the recovery process may lead to material failure, i.e. partial tears or complete rupture. Additionally, studies show that tendons have a maximum modulus of approximately 800 MPa; thus, any additional loading will not result in a significant increase in modulus strength.[12] These results may change current physical therapy practices, since aggressive training of the tendon does not strengthen the structure beyond its baseline mechanical properties; therefore, patients are still as susceptible to tendon overuse and injuries.
See also
References
- ^ Ellenbecker, Todd, "Effective Functional Progressions in Sport Rehabilitation", Human Kinetics 2009, ISBN 0-7360-6381-1
- ^ Frost, Harold "New targets for fascial, ligament and tendon research: A perspective from the Utah paradigm of skeletal physiology" J Musculoskel Neuron Interact 2003; 3(3):201–209
- ^ Frost, Harold "The physiology of cartilagenous, fibrous, and bony tissue. C.C. Thomas, 1972
- ^ Frost, Harold "The physiology of cartilagenous, fibrous, and bony tissue. C.C. Thomas, 1972, page 176
- ^ Frost, Harold "Does the anterior cruciate have a modeling threshold? A case for the affirmative". J Musculoskel Neuron Interact 2001; 2(2):131–136
- ^ Nutt, John Joseph (1913). Diseases and Deformities of the Foot. E.B. Treat & Company.
davis's law.
- ^ Kynett, H.H.; Butler, S.W.; Brinton, D.G. (1862). Medical and Surgical Reporter. Vol. 8. p. 518. Retrieved 2017-02-23.
- ^ Bauer, L. (1868). Lectures on Orthopaedic Surgery: Delivered at the Brooklyn Medical and Surgical Institute. Wood. Retrieved 2017-02-23.
- ^ London Medical Gazette: Or, Journal of Practical Medicine. Vol. 48. 1851. Retrieved 2017-02-23.
- ^ "Whonamedit – dictionary of medical eponyms". whonamedit.com. Retrieved 2017-02-23.
- ^ N. Reeves; C. Maganaris; G. Ferretti; M. Narici (2005). "Influence of 90-day simulated microgravity on human tendon mechanical properties and the effect of resistive countermeasures" (PDF). J Appl Physiol. 98 (6): 2278–2286. doi:10.1152/japplphysiol.01266.2004. hdl:11379/25397. PMID 15705722.
- ^ a b T. Wren; S. Yerby; G. Beaupré; C. Carter (2001). "Mechanical properties of the human Achilles tendon". Clinical Biomechanics. 16 (3): 245–251. doi:10.1016/s0268-0033(00)00089-9. PMID 11240060.
- ^ R. James; G. Kesturu; G. Balian; B. Chhabra (2008). "Tendon: biology, biomechanics, repair, growth factors, and evolving treatment options". J Hand Surg. 33 (1): 102–112. doi:10.1016/j.jhsa.2007.09.007. PMID 18261674.
- Davis, Henry Gassett, Conservative Surgery New York: D. Appleton & Co.; 1867
- Nutt, John Joseph, Diseases and deformities of the foot. New York: E. B. Treat & Co.; 1915, pp. 157–158. (Out of copyright. Available as a pdf in total via Google books).
- Spencer AM, Practical podiatric orthopedic procedures. Cleveland: Ohio College of Podiatric Medicine; 1978.
- Tippett, Steven R. and Michael L. Voight, Functional Progression for Sport Rehabilitation. Champaigne IL: Human Kinetics; 1995, ISBN 0-87322-660-7, p. 4.
