Banach space
In mathematics, more specifically in functional analysis, a Banach space (pronounced [ˈbanax]) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well-defined limit that is within the space.
Banach spaces are named after the Polish mathematician Stefan Banach, who introduced this concept and studied it systematically in 1920–1922 along with Hans Hahn and Eduard Helly.[1] Maurice René Fréchet was the first to use the term "Banach space" and Banach in turn then coined the term "Fréchet space".[2] Banach spaces originally grew out of the study of function spaces by Hilbert, Fréchet, and Riesz earlier in the century. Banach spaces play a central role in functional analysis. In other areas of analysis, the spaces under study are often Banach spaces.
Definition
A Banach space is a complete normed space A normed space is a pair[note 1] consisting of a vector space over a scalar field (where is commonly or ) together with a distinguished[note 2] norm Like all norms, this norm induces a translation invariant[note 3] distance function, called the canonical or (norm) induced metric, defined for all vectors by[note 4] This makes into a metric space A sequence is called Cauchy in or -Cauchy or -Cauchy if for every real there exists some index such that whenever and are greater than The normed space is called a Banach space and the canonical metric is called a complete metric if is a complete metric space, which by definition means for every Cauchy sequence in there exists some such that where because this sequence's convergence to can equivalently be expressed as:
The norm of a normed space is called a complete norm if is a Banach space.
- L-semi-inner product
For any normed space there exists an L-semi-inner product on such that for all in general, there may be infinitely many L-semi-inner products that satisfy this condition. L-semi-inner products are a generalization of inner products, which are what fundamentally distinguish Hilbert spaces from all other Banach spaces. This shows that all normed spaces (and hence all Banach spaces) can be considered as being generalizations of (pre-)Hilbert spaces.
- Characterization in terms of series
The vector space structure allows one to relate the behavior of Cauchy sequences to that of converging series of vectors. A normed space is a Banach space if and only if each absolutely convergent series in converges to a value that lies within [3]
Topology
The canonical metric of a normed space induces the usual metric topology on which is referred to as the canonical or norm induced topology. Every normed space is automatically assumed to carry this Hausdorff topology, unless indicated otherwise. With this topology, every Banach space is a Baire space, although there exist normed spaces that are Baire but not Banach.[4] The norm is always a continuous function with respect to the topology that it induces.
The open and closed balls of radius centered at a point are, respectively, the sets Any such ball is a convex and bounded subset of but a compact ball / neighborhood exists if and only if is a finite-dimensional vector space. In particular, no infinite–dimensional normed space can be locally compact or have the Heine–Borel property. If is a vector and is a scalar then Using shows that this norm-induced topology is translation invariant, which means that for any and the subset is open (respectively, closed) in if and only if this is true of its translation Consequently, the norm induced topology is completely determined by any neighbourhood basis at the origin. Some common neighborhood bases at the origin include: where is a sequence in of positive real numbers that converges to in (such as or for instance). So for example, every open subset of can be written as a union indexed by some subset where every may be picked from the aforementioned sequence (the open balls can be replaced with closed balls, although then the indexing set and radii may also need to be replaced). Additionally, can always be chosen to be countable if is a separable space, which by definition means that contains some countable dense subset.
- Homeomorphism classes of separable Banach spaces
All finite–dimensional normed spaces are separable Banach spaces and any two Banach spaces of the same finite dimension are linearly homeomorphic. Every separable infinite–dimensional Hilbert space is linearly isometrically isomorphic to the separable Hilbert sequence space with its usual norm
The Anderson–Kadec theorem states that every infinite–dimensional separable Fréchet space is homeomorphic to the product space of countably many copies of (this homeomorphism need not be a linear map).[5][6] Thus all infinite–dimensional separable Fréchet spaces are homeomorphic to each other (or said differently, their topology is unique up to a homeomorphism). Since every Banach space is a Fréchet space, this is also true of all infinite–dimensional separable Banach spaces, including In fact, is even homeomorphic to its own unit sphere which stands in sharp contrast to finite–dimensional spaces (the Euclidean plane is not homeomorphic to the unit circle, for instance).
This pattern in homeomorphism classes extends to generalizations of metrizable (locally Euclidean) topological manifolds known as metric Banach manifolds, which are metric spaces that are around every point, locally homeomorphic to some open subset of a given Banach space (metric Hilbert manifolds and metric Fréchet manifolds are defined similarly).[6] For example, every open subset of a Banach space is canonically a metric Banach manifold modeled on since the inclusion map is an open local homeomorphism. Using Hilbert space microbundles, David Henderson showed[7] in 1969 that every metric manifold modeled on a separable infinite–dimensional Banach (or Fréchet) space can be topologically embedded as an open subset of and, consequently, also admits a unique smooth structure making it into a Hilbert manifold.
- Compact and convex subsets
There is a compact subset of whose convex hull is not closed and thus also not compact (see this footnote[note 5] for an example).[8] However, like in all Banach spaces, the closed convex hull of this (and every other) compact subset will be compact.[9] But if a normed space is not complete then it is in general not guaranteed that will be compact whenever is; an example[note 5] can even be found in a (non-complete) pre-Hilbert vector subspace of
- As a topological vector space
This norm-induced topology also makes into what is known as a topological vector space (TVS), which by definition is a vector space endowed with a topology making the operations of addition and scalar multiplication continuous. It is emphasized that the TVS is only a vector space together with a certain type of topology; that is to say, when considered as a TVS, it is not associated with any particular norm or metric (both of which are "forgotten"). This Hausdorff TVS is even locally convex because the set of all open balls centered at the origin forms a neighbourhood basis at the origin consisting of convex balanced open sets. This TVS is also normable, which by definition refers to any TVS whose topology is induced by some (possibly unknown) norm. Normable TVSs are characterized by being Hausdorff and having a bounded convex neighborhood of the origin. All Banach spaces are barrelled spaces, which means that every barrel is neighborhood of the origin (all closed balls centered at the origin are barrels, for example) and guarantees that the Banach–Steinhaus theorem holds.
- Comparison of complete metrizable vector topologies
The open mapping theorem implies that if and are topologies on that make both and into complete metrizable TVS (for example, Banach or Fréchet spaces) and if one topology is finer or coarser than the other then they must be equal (that is, if or then ).[10] So for example, if and are Banach spaces with topologies and and if one of these spaces has some open ball that is also an open subset of the other space (or equivalently, if one of or is continuous) then their topologies are identical and their norms are equivalent.
Completeness
- Complete norms and equivalent norms
Two norms, and on a vector space are said to be equivalent if they induce the same topology;[11] this happens if and only if there exist positive real numbers such that for all If and are two equivalent norms on a vector space then is a Banach space if and only if is a Banach space. See this footnote for an example of a continuous norm on a Banach space that is not equivalent to that Banach space's given norm.[note 6][11] All norms on a finite-dimensional vector space are equivalent and every finite-dimensional normed space is a Banach space.[12]
- Complete norms vs complete metrics
A metric on a vector space is induced by a norm on if and only if is translation invariant[note 3] and absolutely homogeneous, which means that for all scalars and all in which case the function defines a norm on and the canonical metric induced by is equal to
Suppose that is a normed space and that is the norm topology induced on Suppose that is any metric on such that the topology that induces on is equal to If is translation invariant[note 3] then is a Banach space if and only if is a complete metric space.[13] If is not translation invariant, then it may be possible for to be a Banach space but for to not be a complete metric space[14] (see this footnote[note 7] for an example). In contrast, a theorem of Klee,[15][16][note 8] which also applies to all metrizable topological vector spaces, implies that if there exists any[note 9] complete metric on that induces the norm topology on then is a Banach space.
A Fréchet space is a locally convex topological vector space whose topology is induced by some translation-invariant complete metric. Every Banach space is a Fréchet space but not conversely; indeed, there even exist Fréchet spaces on which no norm is a continuous function (such as the space of real sequences with the product topology). However, the topology of every Fréchet space is induced by some countable family of real-valued (necessarily continuous) maps called seminorms, which are generalizations of norms. It is even possible for a Fréchet space to have a topology that is induced by a countable family of norms (such norms would necessarily be continuous)[note 10][17] but to not be a Banach/normable space because its topology can not be defined by any single norm. An example of such a space is the Fréchet space whose definition can be found in the article on spaces of test functions and distributions.
Complete norms vs complete topological vector spaces
There is another notion of completeness besides metric completeness and that is the notion of a complete topological vector space (TVS) or TVS-completeness, which uses the theory of uniform spaces. Specifically, the notion of TVS-completeness uses a unique translation-invariant uniformity, called the canonical uniformity, that depends only on vector subtraction and the topology that the vector space is endowed with, and so in particular, this notion of TVS completeness is independent of whatever norm induced the topology (and even applies to TVSs that are not even metrizable). Every Banach space is a complete TVS. Moreover, a normed space is a Banach space (that is, its norm-induced metric is complete) if and only if it is complete as a topological vector space. If is a metrizable topological vector space (such as any norm induced topology, for example), then is a complete TVS if and only if it is a sequentially complete TVS, meaning that it is enough to check that every Cauchy sequence in converges in to some point of (that is, there is no need to consider the more general notion of arbitrary Cauchy nets).
If is a topological vector space whose topology is induced by some (possibly unknown) norm (such spaces are called normable), then is a complete topological vector space if and only if may be assigned a norm that induces on the topology and also makes into a Banach space. A Hausdorff locally convex topological vector space is normable if and only if its strong dual space is normable,[18] in which case is a Banach space ( denotes the strong dual space of whose topology is a generalization of the dual norm-induced topology on the continuous dual space ; see this footnote[note 11] for more details). If is a metrizable locally convex TVS, then is normable if and only if is a Fréchet–Urysohn space.[19] This shows that in the category of locally convex TVSs, Banach spaces are exactly those complete spaces that are both metrizable and have metrizable strong dual spaces.
Completions
Every normed space can be isometrically embedded onto a dense vector subspace of some Banach space, where this Banach space is called a completion of the normed space. This Hausdorff completion is unique up to isometric isomorphism.
More precisely, for every normed space there exist a Banach space and a mapping such that is an isometric mapping and is dense in If is another Banach space such that there is an isometric isomorphism from onto a dense subset of then is isometrically isomorphic to This Banach space is the Hausdorff completion of the normed space The underlying metric space for is the same as the metric completion of with the vector space operations extended from to The completion of is sometimes denoted by
General theory
Linear operators, isomorphisms
If and are normed spaces over the same ground field the set of all continuous -linear maps is denoted by In infinite-dimensional spaces, not all linear maps are continuous. A linear mapping from a normed space to another normed space is continuous if and only if it is bounded on the closed unit ball of Thus, the vector space can be given the operator norm
For a Banach space, the space is a Banach space with respect to this norm. In categorical contexts, it is sometimes convenient to restrict the function space between two Banach spaces to only the short maps; in that case the space reappears as a natural bifunctor.[20]
If is a Banach space, the space forms a unital Banach algebra; the multiplication operation is given by the composition of linear maps.
If and are normed spaces, they are isomorphic normed spaces if there exists a linear bijection such that and its inverse are continuous. If one of the two spaces or is complete (or reflexive, separable, etc.) then so is the other space. Two normed spaces and are isometrically isomorphic if in addition, is an isometry, that is, for every in The Banach–Mazur distance between two isomorphic but not isometric spaces and gives a measure of how much the two spaces and differ.
Continuous and bounded linear functions and seminorms
Every continuous linear operator is a bounded linear operator and if dealing only with normed spaces then the converse is also true. That is, a linear operator between two normed spaces is bounded if and only if it is a continuous function. So in particular, because the scalar field (which is or ) is a normed space, a linear functional on a normed space is a bounded linear functional if and only if it is a continuous linear functional. This allows for continuity-related results (like those below) to be applied to Banach spaces. Although boundedness is the same as continuity for linear maps between normed spaces, the term "bounded" is more commonly used when dealing primarily with Banach spaces.
If is a subadditive function (such as a norm, a sublinear function, or real linear functional), then[21] is continuous at the origin if and only if is uniformly continuous on all of ; and if in addition then is continuous if and only if its absolute value is continuous, which happens if and only if is an open subset of [21][note 12] And very importantly for applying the Hahn–Banach theorem, a linear functional is continuous if and only if this is true of its real part and moreover, and the real part completely determines which is why the Hahn–Banach theorem is often stated only for real linear functionals. Also, a linear functional on is continuous if and only if the seminorm is continuous, which happens if and only if there exists a continuous seminorm such that ; this last statement involving the linear functional and seminorm is encountered in many versions of the Hahn–Banach theorem.
Basic notions
The Cartesian product of two normed spaces is not canonically equipped with a norm. However, several equivalent norms are commonly used,[22] such as which correspond (respectively) to the coproduct and product in the category of Banach spaces and short maps (discussed above).[20] For finite (co)products, these norms give rise to isomorphic normed spaces, and the product (or the direct sum ) is complete if and only if the two factors are complete.
If is a closed linear subspace of a normed space there is a natural norm on the quotient space
The quotient is a Banach space when is complete.[23] The quotient map from onto sending to its class is linear, onto and has norm except when in which case the quotient is the null space.
The closed linear subspace of is said to be a complemented subspace of if is the range of a surjective bounded linear projection In this case, the space is isomorphic to the direct sum of and the kernel of the projection
Suppose that and are Banach spaces and that There exists a canonical factorization of as[23] where the first map is the quotient map, and the second map sends every class in the quotient to the image in This is well defined because all elements in the same class have the same image. The mapping is a linear bijection from onto the range whose inverse need not be bounded.
Classical spaces
Basic examples[24] of Banach spaces include: the Lp spaces and their special cases, the sequence spaces that consist of scalar sequences indexed by natural numbers ; among them, the space of absolutely summable sequences and the space of square summable sequences; the space of sequences tending to zero and the space of bounded sequences; the space of continuous scalar functions on a compact Hausdorff space equipped with the max norm,
According to the Banach–Mazur theorem, every Banach space is isometrically isomorphic to a subspace of some [25] For every separable Banach space there is a closed subspace of such that [26]
Any Hilbert space serves as an example of a Banach space. A Hilbert space on is complete for a norm of the form where is the inner product, linear in its first argument that satisfies the following:
For example, the space is a Hilbert space.
The Hardy spaces, the Sobolev spaces are examples of Banach spaces that are related to spaces and have additional structure. They are important in different branches of analysis, Harmonic analysis and Partial differential equations among others.
Banach algebras
A Banach algebra is a Banach space over or together with a structure of algebra over , such that the product map is continuous. An equivalent norm on can be found so that for all
Examples
- The Banach space with the pointwise product, is a Banach algebra.
- The disk algebra consists of functions holomorphic in the open unit disk and continuous on its closure: Equipped with the max norm on the disk algebra is a closed subalgebra of
- The Wiener algebra is the algebra of functions on the unit circle with absolutely convergent Fourier series. Via the map associating a function on to the sequence of its Fourier coefficients, this algebra is isomorphic to the Banach algebra where the product is the convolution of sequences.
- For every Banach space the space of bounded linear operators on with the composition of maps as product, is a Banach algebra.
- A C*-algebra is a complex Banach algebra with an antilinear involution such that The space of bounded linear operators on a Hilbert space is a fundamental example of C*-algebra. The Gelfand–Naimark theorem states that every C*-algebra is isometrically isomorphic to a C*-subalgebra of some The space of complex continuous functions on a compact Hausdorff space is an example of commutative C*-algebra, where the involution associates to every function its complex conjugate
Dual space
If is a normed space and the underlying field (either the real or the complex numbers), the continuous dual space is the space of continuous linear maps from into or continuous linear functionals. The notation for the continuous dual is in this article.[27] Since is a Banach space (using the absolute value as norm), the dual is a Banach space, for every normed space The Dixmier–Ng theorem characterizes the dual spaces of Banach spaces.
The main tool for proving the existence of continuous linear functionals is the Hahn–Banach theorem.
Hahn–Banach theorem — Let be a vector space over the field Let further
- be a linear subspace,
- be a sublinear function and
- be a linear functional so that for all
Then, there exists a linear functional so that
In particular, every continuous linear functional on a subspace of a normed space can be continuously extended to the whole space, without increasing the norm of the functional.[28] An important special case is the following: for every vector in a normed space there exists a continuous linear functional on such that
When is not equal to the vector, the functional must have norm one, and is called a norming functional for
The Hahn–Banach separation theorem states that two disjoint non-empty convex sets in a real Banach space, one of them open, can be separated by a closed affine hyperplane. The open convex set lies strictly on one side of the hyperplane, the second convex set lies on the other side but may touch the hyperplane.[29]
A subset in a Banach space is total if the linear span of is dense in The subset is total in if and only if the only continuous linear functional that vanishes on is the functional: this equivalence follows from the Hahn–Banach theorem.
If is the direct sum of two closed linear subspaces and then the dual of is isomorphic to the direct sum of the duals of and [30] If is a closed linear subspace in one can associate the orthogonal of in the dual,
The orthogonal is a closed linear subspace of the dual. The dual of is isometrically isomorphic to The dual of is isometrically isomorphic to [31]
The dual of a separable Banach space need not be separable, but:
When is separable, the above criterion for totality can be used for proving the existence of a countable total subset in
Weak topologies
The weak topology on a Banach space is the coarsest topology on for which all elements in the continuous dual space are continuous. The norm topology is therefore finer than the weak topology. It follows from the Hahn–Banach separation theorem that the weak topology is Hausdorff, and that a norm-closed convex subset of a Banach space is also weakly closed.[33] A norm-continuous linear map between two Banach spaces and is also weakly continuous, that is, continuous from the weak topology of to that of [34]
If is infinite-dimensional, there exist linear maps which are not continuous. The space of all linear maps from to the underlying field (this space is called the algebraic dual space, to distinguish it from also induces a topology on which is finer than the weak topology, and much less used in functional analysis.
On a dual space there is a topology weaker than the weak topology of called weak* topology. It is the coarsest topology on for which all evaluation maps where ranges over are continuous. Its importance comes from the Banach–Alaoglu theorem.
Banach–Alaoglu theorem — Let be a normed vector space. Then the closed unit ball of the dual space is compact in the weak* topology.
The Banach–Alaoglu theorem can be proved using Tychonoff's theorem about infinite products of compact Hausdorff spaces. When is separable, the unit ball of the dual is a metrizable compact in the weak* topology.[35]
Examples of dual spaces
The dual of is isometrically isomorphic to : for every bounded linear functional on there is a unique element such that
The dual of is isometrically isomorphic to . The dual of Lebesgue space is isometrically isomorphic to when and
For every vector in a Hilbert space the mapping
defines a continuous linear functional on The Riesz representation theorem states that every continuous linear functional on is of the form for a uniquely defined vector in The mapping is an antilinear isometric bijection from onto its dual When the scalars are real, this map is an isometric isomorphism.
When is a compact Hausdorff topological space, the dual of is the space of Radon measures in the sense of Bourbaki.[36] The subset of consisting of non-negative measures of mass 1 (probability measures) is a convex w*-closed subset of the unit ball of The extreme points of are the Dirac measures on The set of Dirac measures on equipped with the w*-topology, is homeomorphic to
Banach–Stone Theorem — If and are compact Hausdorff spaces and if and are isometrically isomorphic, then the topological spaces and are homeomorphic.[37][38]
The result has been extended by Amir[39] and Cambern[40] to the case when the multiplicative Banach–Mazur distance between and is The theorem is no longer true when the distance is [41]
In the commutative Banach algebra the maximal ideals are precisely kernels of Dirac measures on
More generally, by the Gelfand–Mazur theorem, the maximal ideals of a unital commutative Banach algebra can be identified with its characters—not merely as sets but as topological spaces: the former with the hull-kernel topology and the latter with the w*-topology. In this identification, the maximal ideal space can be viewed as a w*-compact subset of the unit ball in the dual
Theorem — If is a compact Hausdorff space, then the maximal ideal space of the Banach algebra is homeomorphic to [37]
Not every unital commutative Banach algebra is of the form for some compact Hausdorff space However, this statement holds if one places in the smaller category of commutative C*-algebras. Gelfand's representation theorem for commutative C*-algebras states that every commutative unital C*-algebra is isometrically isomorphic to a space.[42] The Hausdorff compact space here is again the maximal ideal space, also called the spectrum of in the C*-algebra context.
Bidual
If is a normed space, the (continuous) dual of the dual is called bidual, or second dual of For every normed space there is a natural map,
This defines as a continuous linear functional on that is, an element of The map is a linear map from to As a consequence of the existence of a norming functional for every this map is isometric, thus injective.
For example, the dual of is identified with and the dual of is identified with the space of bounded scalar sequences. Under these identifications, is the inclusion map from to It is indeed isometric, but not onto.
If is surjective, then the normed space is called reflexive (see below). Being the dual of a normed space, the bidual is complete, therefore, every reflexive normed space is a Banach space.
Using the isometric embedding it is customary to consider a normed space as a subset of its bidual. When is a Banach space, it is viewed as a closed linear subspace of If is not reflexive, the unit ball of is a proper subset of the unit ball of The Goldstine theorem states that the unit ball of a normed space is weakly*-dense in the unit ball of the bidual. In other words, for every in the bidual, there exists a net in so that
The net may be replaced by a weakly*-convergent sequence when the dual is separable. On the other hand, elements of the bidual of that are not in cannot be weak*-limit of sequences in since is weakly sequentially complete.
Banach's theorems
Here are the main general results about Banach spaces that go back to the time of Banach's book (Banach (1932)) and are related to the Baire category theorem. According to this theorem, a complete metric space (such as a Banach space, a Fréchet space or an F-space) cannot be equal to a union of countably many closed subsets with empty interiors. Therefore, a Banach space cannot be the union of countably many closed subspaces, unless it is already equal to one of them; a Banach space with a countable Hamel basis is finite-dimensional.
Banach–Steinhaus Theorem — Let be a Banach space and be a normed vector space. Suppose that is a collection of continuous linear operators from to The uniform boundedness principle states that if for all in we have then
The Banach–Steinhaus theorem is not limited to Banach spaces. It can be extended for example to the case where is a Fréchet space, provided the conclusion is modified as follows: under the same hypothesis, there exists a neighborhood of in such that all in are uniformly bounded on
The Open Mapping Theorem — Let and be Banach spaces and be a surjective continuous linear operator, then is an open map.
Corollary — Every one-to-one bounded linear operator from a Banach space onto a Banach space is an isomorphism.
The First Isomorphism Theorem for Banach spaces — Suppose that and are Banach spaces and that Suppose further that the range of is closed in Then is isomorphic to
This result is a direct consequence of the preceding Banach isomorphism theorem and of the canonical factorization of bounded linear maps.
Corollary — If a Banach space is the internal direct sum of closed subspaces then is isomorphic to
This is another consequence of Banach's isomorphism theorem, applied to the continuous bijection from onto sending to the sum
The Closed Graph Theorem — Let be a linear mapping between Banach spaces. The graph of is closed in if and only if is continuous.
Reflexivity
The normed space is called reflexive when the natural map is surjective. Reflexive normed spaces are Banach spaces.
Theorem — If is a reflexive Banach space, every closed subspace of and every quotient space of are reflexive.
This is a consequence of the Hahn–Banach theorem. Further, by the open mapping theorem, if there is a bounded linear operator from the Banach space onto the Banach space then is reflexive.
Theorem — If is a Banach space, then is reflexive if and only if is reflexive.
Corollary — Let be a reflexive Banach space. Then is separable if and only if is separable.
Indeed, if the dual of a Banach space is separable, then is separable. If is reflexive and separable, then the dual of is separable, so is separable.
Theorem — Suppose that are normed spaces and that Then is reflexive if and only if each is reflexive.
Hilbert spaces are reflexive. The spaces are reflexive when More generally, uniformly convex spaces are reflexive, by the Milman–Pettis theorem. The spaces are not reflexive. In these examples of non-reflexive spaces the bidual is "much larger" than Namely, under the natural isometric embedding of into given by the Hahn–Banach theorem, the quotient is infinite-dimensional, and even nonseparable. However, Robert C. James has constructed an example[43] of a non-reflexive space, usually called "the James space" and denoted by [44] such that the quotient is one-dimensional. Furthermore, this space is isometrically isomorphic to its bidual.
Theorem — A Banach space is reflexive if and only if its unit ball is compact in the weak topology.
When is reflexive, it follows that all closed and bounded convex subsets of are weakly compact. In a Hilbert space the weak compactness of the unit ball is very often used in the following way: every bounded sequence in has weakly convergent subsequences.
Weak compactness of the unit ball provides a tool for finding solutions in reflexive spaces to certain optimization problems. For example, every convex continuous function on the unit ball of a reflexive space attains its minimum at some point in
As a special case of the preceding result, when is a reflexive space over every continuous linear functional in attains its maximum on the unit ball of The following theorem of Robert C. James provides a converse statement.
James' Theorem — For a Banach space the following two properties are equivalent:
- is reflexive.
- for all in there exists with so that
The theorem can be extended to give a characterization of weakly compact convex sets.
On every non-reflexive Banach space there exist continuous linear functionals that are not norm-attaining. However, the Bishop–Phelps theorem[45] states that norm-attaining functionals are norm dense in the dual of
Weak convergences of sequences
A sequence in a Banach space is weakly convergent to a vector if converges to for every continuous linear functional in the dual The sequence is a weakly Cauchy sequence if converges to a scalar limit for every in A sequence in the dual is weakly* convergent to a functional if converges to for every in Weakly Cauchy sequences, weakly convergent and weakly* convergent sequences are norm bounded, as a consequence of the Banach–Steinhaus theorem.
When the sequence in is a weakly Cauchy sequence, the limit above defines a bounded linear functional on the dual that is, an element of the bidual of and is the limit of in the weak*-topology of the bidual. The Banach space is weakly sequentially complete if every weakly Cauchy sequence is weakly convergent in It follows from the preceding discussion that reflexive spaces are weakly sequentially complete.
Theorem [46] — For every measure the space is weakly sequentially complete.
An orthonormal sequence in a Hilbert space is a simple example of a weakly convergent sequence, with limit equal to the vector. The unit vector basis of for or of is another example of a weakly null sequence, that is, a sequence that converges weakly to For every weakly null sequence in a Banach space, there exists a sequence of convex combinations of vectors from the given sequence that is norm-converging to [47]
The unit vector basis of is not weakly Cauchy. Weakly Cauchy sequences in are weakly convergent, since -spaces are weakly sequentially complete. Actually, weakly convergent sequences in are norm convergent.[48] This means that satisfies Schur's property.
Results involving the basis
Weakly Cauchy sequences and the basis are the opposite cases of the dichotomy established in the following deep result of H. P. Rosenthal.[49]
Theorem[50] — Let be a bounded sequence in a Banach space. Either has a weakly Cauchy subsequence, or it admits a subsequence equivalent to the standard unit vector basis of
A complement to this result is due to Odell and Rosenthal (1975).
Theorem[51] — Let be a separable Banach space. The following are equivalent:
- The space does not contain a closed subspace isomorphic to
- Every element of the bidual is the weak*-limit of a sequence in
By the Goldstine theorem, every element of the unit ball of is weak*-limit of a net in the unit ball of When does not contain every element of is weak*-limit of a sequence in the unit ball of [52]
When the Banach space is separable, the unit ball of the dual equipped with the weak*-topology, is a metrizable compact space [35] and every element in the bidual defines a bounded function on :
This function is continuous for the compact topology of if and only if is actually in considered as subset of Assume in addition for the rest of the paragraph that does not contain By the preceding result of Odell and Rosenthal, the function is the pointwise limit on of a sequence of continuous functions on it is therefore a first Baire class function on The unit ball of the bidual is a pointwise compact subset of the first Baire class on [53]
Sequences, weak and weak* compactness
When is separable, the unit ball of the dual is weak*-compact by the Banach–Alaoglu theorem and metrizable for the weak* topology,[35] hence every bounded sequence in the dual has weakly* convergent subsequences. This applies to separable reflexive spaces, but more is true in this case, as stated below.
The weak topology of a Banach space is metrizable if and only if is finite-dimensional.[54] If the dual is separable, the weak topology of the unit ball of is metrizable. This applies in particular to separable reflexive Banach spaces. Although the weak topology of the unit ball is not metrizable in general, one can characterize weak compactness using sequences.
Eberlein–Šmulian theorem[55] — A set in a Banach space is relatively weakly compact if and only if every sequence in has a weakly convergent subsequence.
A Banach space is reflexive if and only if each bounded sequence in has a weakly convergent subsequence.[56]
A weakly compact subset in is norm-compact. Indeed, every sequence in has weakly convergent subsequences by Eberlein–Šmulian, that are norm convergent by the Schur property of
Type and cotype
A way to classify Banach spaces is through the probabilistic notion of type and cotype, these two measure how far a Banach space is from a Hilbert space.
Schauder bases
A Schauder basis in a Banach space is a sequence of vectors in with the property that for every vector there exist uniquely defined scalars depending on such that
Banach spaces with a Schauder basis are necessarily separable, because the countable set of finite linear combinations with rational coefficients (say) is dense.
It follows from the Banach–Steinhaus theorem that the linear mappings are uniformly bounded by some constant Let denote the coordinate functionals which assign to every in the coordinate of in the above expansion. They are called biorthogonal functionals. When the basis vectors have norm the coordinate functionals have norm in the dual of
Most classical separable spaces have explicit bases. The Haar system is a basis for The trigonometric system is a basis in when The Schauder system is a basis in the space [57] The question of whether the disk algebra has a basis[58] remained open for more than forty years, until Bočkarev showed in 1974 that admits a basis constructed from the Franklin system.[59]
Since every vector in a Banach space with a basis is the limit of with of finite rank and uniformly bounded, the space satisfies the bounded approximation property. The first example by Enflo of a space failing the approximation property was at the same time the first example of a separable Banach space without a Schauder basis.[60]
Robert C. James characterized reflexivity in Banach spaces with a basis: the space with a Schauder basis is reflexive if and only if the basis is both shrinking and boundedly complete.[61] In this case, the biorthogonal functionals form a basis of the dual of
Tensor product
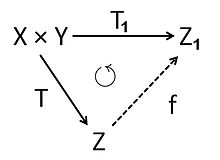
Let and be two -vector spaces. The tensor product of and is a -vector space with a bilinear mapping which has the following universal property:
- If is any bilinear mapping into a -vector space then there exists a unique linear mapping such that
The image under of a couple in is denoted by and called a simple tensor. Every element in is a finite sum of such simple tensors.
There are various norms that can be placed on the tensor product of the underlying vector spaces, amongst others the projective cross norm and injective cross norm introduced by A. Grothendieck in 1955.[62]
In general, the tensor product of complete spaces is not complete again. When working with Banach spaces, it is customary to say that the projective tensor product[63] of two Banach spaces and is the completion of the algebraic tensor product equipped with the projective tensor norm, and similarly for the injective tensor product[64] Grothendieck proved in particular that[65]
where is a compact Hausdorff space, the Banach space of continuous functions from to and the space of Bochner-measurable and integrable functions from to and where the isomorphisms are isometric. The two isomorphisms above are the respective extensions of the map sending the tensor to the vector-valued function
Tensor products and the approximation property
Let be a Banach space. The tensor product is identified isometrically with the closure in of the set of finite rank operators. When has the approximation property, this closure coincides with the space of compact operators on
For every Banach space there is a natural norm linear map obtained by extending the identity map of the algebraic tensor product. Grothendieck related the approximation problem to the question of whether this map is one-to-one when is the dual of Precisely, for every Banach space the map is one-to-one if and only if has the approximation property.[66]
Grothendieck conjectured that and must be different whenever and are infinite-dimensional Banach spaces. This was disproved by Gilles Pisier in 1983.[67] Pisier constructed an infinite-dimensional Banach space such that and are equal. Furthermore, just as Enflo's example, this space is a "hand-made" space that fails to have the approximation property. On the other hand, Szankowski proved that the classical space does not have the approximation property.[68]
Some classification results
Characterizations of Hilbert space among Banach spaces
A necessary and sufficient condition for the norm of a Banach space to be associated to an inner product is the parallelogram identity:
Parallelogram identity — for all
It follows, for example, that the Lebesgue space is a Hilbert space only when If this identity is satisfied, the associated inner product is given by the polarization identity. In the case of real scalars, this gives:
For complex scalars, defining the inner product so as to be -linear in antilinear in the polarization identity gives:
To see that the parallelogram law is sufficient, one observes in the real case that is symmetric, and in the complex case, that it satisfies the Hermitian symmetry property and The parallelogram law implies that is additive in It follows that it is linear over the rationals, thus linear by continuity.
Several characterizations of spaces isomorphic (rather than isometric) to Hilbert spaces are available. The parallelogram law can be extended to more than two vectors, and weakened by the introduction of a two-sided inequality with a constant : Kwapień proved that if for every integer and all families of vectors then the Banach space is isomorphic to a Hilbert space.[69] Here, denotes the average over the possible choices of signs In the same article, Kwapień proved that the validity of a Banach-valued Parseval's theorem for the Fourier transform characterizes Banach spaces isomorphic to Hilbert spaces.
Lindenstrauss and Tzafriri proved that a Banach space in which every closed linear subspace is complemented (that is, is the range of a bounded linear projection) is isomorphic to a Hilbert space.[70] The proof rests upon Dvoretzky's theorem about Euclidean sections of high-dimensional centrally symmetric convex bodies. In other words, Dvoretzky's theorem states that for every integer any finite-dimensional normed space, with dimension sufficiently large compared to contains subspaces nearly isometric to the -dimensional Euclidean space.
The next result gives the solution of the so-called homogeneous space problem. An infinite-dimensional Banach space is said to be homogeneous if it is isomorphic to all its infinite-dimensional closed subspaces. A Banach space isomorphic to is homogeneous, and Banach asked for the converse.[71]
Theorem[72] — A Banach space isomorphic to all its infinite-dimensional closed subspaces is isomorphic to a separable Hilbert space.
An infinite-dimensional Banach space is hereditarily indecomposable when no subspace of it can be isomorphic to the direct sum of two infinite-dimensional Banach spaces. The Gowers dichotomy theorem[72] asserts that every infinite-dimensional Banach space contains, either a subspace with unconditional basis, or a hereditarily indecomposable subspace and in particular, is not isomorphic to its closed hyperplanes.[73] If is homogeneous, it must therefore have an unconditional basis. It follows then from the partial solution obtained by Komorowski and Tomczak–Jaegermann, for spaces with an unconditional basis,[74] that is isomorphic to
Metric classification
If is an isometry from the Banach space onto the Banach space (where both and are vector spaces over ), then the Mazur–Ulam theorem states that must be an affine transformation. In particular, if this is maps the zero of to the zero of then must be linear. This result implies that the metric in Banach spaces, and more generally in normed spaces, completely captures their linear structure.
Topological classification
Finite dimensional Banach spaces are homeomorphic as topological spaces, if and only if they have the same dimension as real vector spaces.
Anderson–Kadec theorem (1965–66) proves[75] that any two infinite-dimensional separable Banach spaces are homeomorphic as topological spaces. Kadec's theorem was extended by Torunczyk, who proved[76] that any two Banach spaces are homeomorphic if and only if they have the same density character, the minimum cardinality of a dense subset.
Spaces of continuous functions
When two compact Hausdorff spaces and are homeomorphic, the Banach spaces and are isometric. Conversely, when is not homeomorphic to the (multiplicative) Banach–Mazur distance between and must be greater than or equal to see above the results by Amir and Cambern. Although uncountable compact metric spaces can have different homeomorphy types, one has the following result due to Milutin:[77]
Theorem[78] — Let be an uncountable compact metric space. Then is isomorphic to
The situation is different for countably infinite compact Hausdorff spaces. Every countably infinite compact is homeomorphic to some closed interval of ordinal numbers equipped with the order topology, where is a countably infinite ordinal.[79] The Banach space is then isometric to C(⟨1, α⟩). When are two countably infinite ordinals, and assuming the spaces C(⟨1, α⟩) and C(⟨1, β⟩) are isomorphic if and only if β < αω.[80] For example, the Banach spaces are mutually non-isomorphic.
Examples
Glossary of symbols for the table below:
- denotes the field of real numbers or complex numbers
- is a compact Hausdorff space.
- are real numbers with that are Hölder conjugates, meaning that they satisfy and thus also
- is a -algebra of sets.
- is an algebra of sets (for spaces only requiring finite additivity, such as the ba space).
- is a measure with variation A positive measure is a real-valued positive set function defined on a -algebra which is countably additive.
| Classical Banach spaces | ||||||
| Dual space | Reflexive | weakly sequentially complete | Norm | Notes | ||
|---|---|---|---|---|---|---|
| Yes | Yes | Euclidean space | ||||
| Yes | Yes | |||||
| Yes | Yes | |||||
| Yes | Yes | |||||
| No | Yes | |||||
| No | No | |||||
| No | No | |||||
| No | No | Isomorphic but not isometric to | ||||
| No | Yes | Isometrically isomorphic to | ||||
| No | Yes | Isometrically isomorphic to | ||||
| No | No | Isometrically isomorphic to | ||||
| No | No | Isometrically isomorphic to | ||||
| No | No | |||||
| No | No | |||||
| ? | No | Yes | ||||
| ? | No | Yes | A closed subspace of | |||
| ? | No | Yes | A closed subspace of | |||
| Yes | Yes | |||||
| No | Yes | The dual is if is -finite. | ||||
| ? | No | Yes | is the total variation of | |||
| ? | No | Yes | consists of functions such that | |||
| No | Yes | Isomorphic to the Sobolev space | ||||
| No | No | Isomorphic to essentially by Taylor's theorem. | ||||
Derivatives
Several concepts of a derivative may be defined on a Banach space. See the articles on the Fréchet derivative and the Gateaux derivative for details. The Fréchet derivative allows for an extension of the concept of a total derivative to Banach spaces. The Gateaux derivative allows for an extension of a directional derivative to locally convex topological vector spaces. Fréchet differentiability is a stronger condition than Gateaux differentiability. The quasi-derivative is another generalization of directional derivative that implies a stronger condition than Gateaux differentiability, but a weaker condition than Fréchet differentiability.
Generalizations
Several important spaces in functional analysis, for instance the space of all infinitely often differentiable functions or the space of all distributions on are complete but are not normed vector spaces and hence not Banach spaces. In Fréchet spaces one still has a complete metric, while LF-spaces are complete uniform vector spaces arising as limits of Fréchet spaces.
See also
- Space (mathematics) – Mathematical set with some added structure
- Fréchet space – A locally convex topological vector space that is also a complete metric space
- Hardy space – Concept within complex analysis
- Hilbert space – Type of topological vector space
- L-semi-inner product – Generalization of inner products that applies to all normed spaces
- space – Function spaces generalizing finite-dimensional p norm spaces
- Sobolev space – Vector space of functions in mathematics
- Banach lattice – Banach space with a compatible structure of a lattice
- Banach disk
- Banach manifold – Manifold modeled on Banach spaces
- Banach bundle – vector bundle whose fibres form Banach spaces
- Distortion problem
- Interpolation space
- Locally convex topological vector space – A vector space with a topology defined by convex open sets
- Modulus and characteristic of convexity
- Smith space – complete compactly generated locally convex space having a universal compact set
- Topological vector space – Vector space with a notion of nearness
- Tsirelson space
Notes
- ^ It is common to read " is a normed space" instead of the more technically correct but (usually) pedantic " is a normed space", especially if the norm is well known (for example, such as with spaces) or when there is no particular need to choose any one (equivalent) norm over any other (especially in the more abstract theory of topological vector spaces), in which case this norm (if needed) is often automatically assumed to be denoted by However, in situations where emphasis is placed on the norm, it is common to see written instead of The technically correct definition of normed spaces as pairs may also become important in the context of category theory where the distinction between the categories of normed spaces, normable spaces, metric spaces, TVSs, topological spaces, etc. is usually important.
- ^ This means that if the norm is replaced with a different norm on then is not the same normed space as not even if the norms are equivalent. However, equivalence of norms on a given vector space does form an equivalence relation.
- ^ a b c A metric on a vector space is said to be translation invariant if for all vectors This happens if and only if for all vectors A metric that is induced by a norm is always translation invariant.
- ^ Because for all it is always true that for all So the order of and in this definition does not matter.
- ^ a b Let be the separable Hilbert space of square-summable sequences with the usual norm and let be the standard orthonormal basis (that is at the -coordinate). The closed set is compact (because it is sequentially compact) but its convex hull is not a closed set because belongs to the closure of in but (since every sequence is a finite convex combination of elements of and so for all but finitely many coordinates, which is not true of ). However, like in all complete Hausdorff locally convex spaces, the closed convex hull of this compact subset is compact. The vector subspace is a pre-Hilbert space when endowed with the substructure that the Hilbert space induces on it but is not complete and (since ). The closed convex hull of in (here, "closed" means with respect to and not to as before) is equal to which is not compact (because it is not a complete subset). This shows that in a Hausdorff locally convex space that is not complete, the closed convex hull of compact subset might fail to be compact (although it will be precompact/totally bounded).
- ^ Let denote the Banach space of continuous functions with the supremum norm and let denote the topology on induced by The vector space can be identified (via the inclusion map) as a proper dense vector subspace of the space which satisfies for all Let denote the restriction of the L1-norm to which makes this map a norm on (in general, the restriction of any norm to any vector subspace will necessarily again be a norm). The normed space is not a Banach space since its completion is the proper superset Because holds on the map is continuous. Despite this, the norm is not equivalent to the norm (because is complete but is not).
- ^ The normed space is a Banach space where the absolute value is a norm on the real line that induces the usual Euclidean topology on Define a metric on by for all Just like 's induced metric, the metric also induces the usual Euclidean topology on However, is not a complete metric because the sequence defined by is a -Cauchy sequence but it does not converge to any point of As a consequence of not converging, this -Cauchy sequence cannot be a Cauchy sequence in (that is, it is not a Cauchy sequence with respect to the norm ) because if it was -Cauchy, then the fact that is a Banach space would imply that it converges (a contradiction).Narici & Beckenstein 2011, pp. 47–51
- ^ The statement of the theorem is: Let be any metric on a vector space such that the topology induced by on makes into a topological vector space. If is a complete metric space then is a complete topological vector space.
- ^ This metric is not assumed to be translation-invariant. So in particular, this metric does not even have to be induced by a norm.
- ^ A norm (or seminorm) on a topological vector space is continuous if and only if the topology that induces on is coarser than (meaning, ), which happens if and only if there exists some open ball in (such as maybe for example) that is open in
- ^ denotes the continuous dual space of When is endowed with the strong dual space topology, also called the topology of uniform convergence on bounded subsets of then this is indicated by writing (sometimes, the subscript is used instead of ). When is a normed space with norm then this topology is equal to the topology on induced by the dual norm. In this way, the strong topology is a generalization of the usual dual norm-induced topology on
- ^ The fact that being open implies that is continuous simplifies proving continuity because this means that it suffices to show that is open for and at (where ) rather than showing this for all real and all
References
- ^ Bourbaki 1987, V.87
- ^ Narici & Beckenstein 2011, p. 93.
- ^ see Theorem 1.3.9, p. 20 in Megginson (1998).
- ^ Wilansky 2013, p. 29.
- ^ Bessaga & Pełczyński 1975, p. 189
- ^ a b Anderson & Schori 1969, p. 315.
- ^ Henderson 1969.
- ^ Aliprantis & Border 2006, p. 185.
- ^ Trèves 2006, p. 145.
- ^ Trèves 2006, pp. 166–173.
- ^ a b Conrad, Keith. "Equivalence of norms" (PDF). kconrad.math.uconn.edu. Archived (PDF) from the original on 2022-10-09. Retrieved September 7, 2020.
- ^ see Corollary 1.4.18, p. 32 in Megginson (1998).
- ^ Narici & Beckenstein 2011, pp. 47–66.
- ^ Narici & Beckenstein 2011, pp. 47–51.
- ^ Schaefer & Wolff 1999, p. 35.
- ^ Klee, V. L. (1952). "Invariant metrics in groups (solution of a problem of Banach)" (PDF). Proc. Amer. Math. Soc. 3 (3): 484–487. doi:10.1090/s0002-9939-1952-0047250-4. Archived (PDF) from the original on 2022-10-09.
- ^ Trèves 2006, pp. 57–69.
- ^ Trèves 2006, p. 201.
- ^ Gabriyelyan, S.S. "On topological spaces and topological groups with certain local countable networks (2014)
- ^ a b Qiaochu Yuan (June 23, 2012). "Banach spaces (and Lawvere metrics, and closed categories)". Annoying Precision.
- ^ a b Narici & Beckenstein 2011, pp. 192–193.
- ^ Banach (1932, p. 182)
- ^ a b see pp. 17–19 in Carothers (2005).
- ^ see Banach (1932), pp. 11-12.
- ^ see Banach (1932), Th. 9 p. 185.
- ^ see Theorem 6.1, p. 55 in Carothers (2005)
- ^ Several books about functional analysis use the notation for the continuous dual, for example Carothers (2005), Lindenstrauss & Tzafriri (1977), Megginson (1998), Ryan (2002), Wojtaszczyk (1991).
- ^ Theorem 1.9.6, p. 75 in Megginson (1998)
- ^ see also Theorem 2.2.26, p. 179 in Megginson (1998)
- ^ see p. 19 in Carothers (2005).
- ^ Theorems 1.10.16, 1.10.17 pp.94–95 in Megginson (1998)
- ^ Theorem 1.12.11, p. 112 in Megginson (1998)
- ^ Theorem 2.5.16, p. 216 in Megginson (1998).
- ^ see II.A.8, p. 29 in Wojtaszczyk (1991)
- ^ a b c see Theorem 2.6.23, p. 231 in Megginson (1998).
- ^ see N. Bourbaki, (2004), "Integration I", Springer Verlag, ISBN 3-540-41129-1.
- ^ a b Eilenberg, Samuel (1942). "Banach Space Methods in Topology". Annals of Mathematics. 43 (3): 568–579. doi:10.2307/1968812. JSTOR 1968812.
- ^ see also Banach (1932), p. 170 for metrizable and
- ^ Amir, Dan (1965). "On isomorphisms of continuous function spaces". Israel Journal of Mathematics. 3 (4): 205–210. doi:10.1007/bf03008398. S2CID 122294213.
- ^ Cambern, M. (1966). "A generalized Banach–Stone theorem". Proc. Amer. Math. Soc. 17 (2): 396–400. doi:10.1090/s0002-9939-1966-0196471-9. And Cambern, M. (1967). "On isomorphisms with small bound". Proc. Amer. Math. Soc. 18 (6): 1062–1066. doi:10.1090/s0002-9939-1967-0217580-2.
- ^ Cohen, H. B. (1975). "A bound-two isomorphism between Banach spaces". Proc. Amer. Math. Soc. 50: 215–217. doi:10.1090/s0002-9939-1975-0380379-5.
- ^ See for example Arveson, W. (1976). An Invitation to C*-Algebra. Springer-Verlag. ISBN 0-387-90176-0.
- ^ R. C. James (1951). "A non-reflexive Banach space isometric with its second conjugate space". Proc. Natl. Acad. Sci. U.S.A. 37 (3): 174–177. Bibcode:1951PNAS...37..174J. doi:10.1073/pnas.37.3.174. PMC 1063327. PMID 16588998.
- ^ see Lindenstrauss & Tzafriri (1977), p. 25.
- ^ bishop, See E.; Phelps, R. (1961). "A proof that every Banach space is subreflexive". Bull. Amer. Math. Soc. 67: 97–98. doi:10.1090/s0002-9904-1961-10514-4.
- ^ see III.C.14, p. 140 in Wojtaszczyk (1991).
- ^ see Corollary 2, p. 11 in Diestel (1984).
- ^ see p. 85 in Diestel (1984).
- ^ Rosenthal, Haskell P (1974). "A characterization of Banach spaces containing ℓ1". Proc. Natl. Acad. Sci. U.S.A. 71 (6): 2411–2413. arXiv:math.FA/9210205. Bibcode:1974PNAS...71.2411R. doi:10.1073/pnas.71.6.2411. PMC 388466. PMID 16592162. Rosenthal's proof is for real scalars. The complex version of the result is due to L. Dor, in Dor, Leonard E (1975). "On sequences spanning a complex ℓ1 space". Proc. Amer. Math. Soc. 47: 515–516. doi:10.1090/s0002-9939-1975-0358308-x.
- ^ see p. 201 in Diestel (1984).
- ^ Odell, Edward W.; Rosenthal, Haskell P. (1975), "A double-dual characterization of separable Banach spaces containing ℓ1" (PDF), Israel Journal of Mathematics, 20 (3–4): 375–384, doi:10.1007/bf02760341, S2CID 122391702, archived (PDF) from the original on 2022-10-09.
- ^ Odell and Rosenthal, Sublemma p. 378 and Remark p. 379.
- ^ for more on pointwise compact subsets of the Baire class, see Bourgain, Jean; Fremlin, D. H.; Talagrand, Michel (1978), "Pointwise Compact Sets of Baire-Measurable Functions", Am. J. Math., 100 (4): 845–886, doi:10.2307/2373913, JSTOR 2373913.
- ^ see Proposition 2.5.14, p. 215 in Megginson (1998).
- ^ see for example p. 49, II.C.3 in Wojtaszczyk (1991).
- ^ see Corollary 2.8.9, p. 251 in Megginson (1998).
- ^ see Lindenstrauss & Tzafriri (1977) p. 3.
- ^ the question appears p. 238, §3 in Banach's book, Banach (1932).
- ^ see S. V. Bočkarev, "Existence of a basis in the space of functions analytic in the disc, and some properties of Franklin's system". (Russian) Mat. Sb. (N.S.) 95(137) (1974), 3–18, 159.
- ^ see Enflo, P. (1973). "A counterexample to the approximation property in Banach spaces". Acta Math. 130: 309–317. doi:10.1007/bf02392270. S2CID 120530273.
- ^ see R.C. James, "Bases and reflexivity of Banach spaces". Ann. of Math. (2) 52, (1950). 518–527. See also Lindenstrauss & Tzafriri (1977) p. 9.
- ^ see A. Grothendieck, "Produits tensoriels topologiques et espaces nucléaires". Mem. Amer. Math. Soc. 1955 (1955), no. 16, 140 pp., and A. Grothendieck, "Résumé de la théorie métrique des produits tensoriels topologiques". Bol. Soc. Mat. São Paulo 8 1953 1–79.
- ^ see chap. 2, p. 15 in Ryan (2002).
- ^ see chap. 3, p. 45 in Ryan (2002).
- ^ see Example. 2.19, p. 29, and pp. 49–50 in Ryan (2002).
- ^ see Proposition 4.6, p. 74 in Ryan (2002).
- ^ see Pisier, Gilles (1983), "Counterexamples to a conjecture of Grothendieck", Acta Math. 151:181–208.
- ^ see Szankowski, Andrzej (1981), " does not have the approximation property", Acta Math. 147: 89–108. Ryan claims that this result is due to Per Enflo, p. 74 in Ryan (2002).
- ^ see Kwapień, S. (1970), "A linear topological characterization of inner-product spaces", Studia Math. 38:277–278.
- ^ Lindenstrauss, Joram; Tzafriri, Lior (1971). "On the complemented subspaces problem". Israel Journal of Mathematics. 9 (2): 263–269. doi:10.1007/BF02771592.
- ^ see p. 245 in Banach (1932). The homogeneity property is called "propriété (15)" there. Banach writes: "on ne connaît aucun exemple d'espace à une infinité de dimensions qui, sans être isomorphe avec possède la propriété (15)".
- ^ a b Gowers, W. T. (1996), "A new dichotomy for Banach spaces", Geom. Funct. Anal. 6:1083–1093.
- ^ see Gowers, W. T. (1994). "A solution to Banach's hyperplane problem". Bull. London Math. Soc. 26 (6): 523–530. doi:10.1112/blms/26.6.523.
- ^ see Komorowski, Ryszard A.; Tomczak-Jaegermann, Nicole (1995). "Banach spaces without local unconditional structure". Israel Journal of Mathematics. 89 (1–3): 205–226. arXiv:math/9306211. doi:10.1007/bf02808201. S2CID 5220304. and also Komorowski, Ryszard A.; Tomczak-Jaegermann, Nicole (1998). "Erratum to: Banach spaces without local unconditional structure". Israel Journal of Mathematics. 105: 85–92. arXiv:math/9607205. doi:10.1007/bf02780323. S2CID 18565676.
- ^ C. Bessaga, A. Pełczyński (1975). Selected Topics in Infinite-Dimensional Topology. Panstwowe wyd. naukowe. pp. 177–230.
- ^ H. Torunczyk (1981). Characterizing Hilbert Space Topology. Fundamenta Mathematicae. pp. 247–262.
- ^ Milyutin, Alekseĭ A. (1966), "Isomorphism of the spaces of continuous functions over compact sets of the cardinality of the continuum". (Russian) Teor. Funkciĭ Funkcional. Anal. i Priložen. Vyp. 2:150–156.
- ^ Milutin. See also Rosenthal, Haskell P., "The Banach spaces C(K)" in Handbook of the geometry of Banach spaces, Vol. 2, 1547–1602, North-Holland, Amsterdam, 2003.
- ^ One can take α = ωβn, where is the Cantor–Bendixson rank of and is the finite number of points in the -th derived set of See Mazurkiewicz, Stefan; Sierpiński, Wacław (1920), "Contribution à la topologie des ensembles dénombrables", Fundamenta Mathematicae 1: 17–27.
- ^ Bessaga, Czesław; Pełczyński, Aleksander (1960), "Spaces of continuous functions. IV. On isomorphical classification of spaces of continuous functions", Studia Math. 19:53–62.
Bibliography
- Aliprantis, Charalambos D.; Border, Kim C. (2006). Infinite Dimensional Analysis: A Hitchhiker's Guide (Third ed.). Berlin: Springer Science & Business Media. ISBN 978-3-540-29587-7. OCLC 262692874.
- Anderson, R. D.; Schori, R. (1969). "Factors of infinite-dimensional manifolds" (PDF). Transactions of the American Mathematical Society. 142. American Mathematical Society (AMS): 315–330. doi:10.1090/s0002-9947-1969-0246327-5. ISSN 0002-9947.
- Bachman, George; Narici, Lawrence (2000). Functional Analysis (Second ed.). Mineola, New York: Dover Publications. ISBN 978-0486402512. OCLC 829157984.
- Banach, Stefan (1932). Théorie des Opérations Linéaires [Theory of Linear Operations] (PDF). Monografie Matematyczne (in French). Vol. 1. Warszawa: Subwencji Funduszu Kultury Narodowej. Zbl 0005.20901. Archived from the original (PDF) on 2014-01-11. Retrieved 2020-07-11.
- Beauzamy, Bernard (1985) [1982], Introduction to Banach Spaces and their Geometry (Second revised ed.), North-Holland.* Bourbaki, Nicolas (1987) [1981]. Topological Vector Spaces: Chapters 1–5. Éléments de mathématique. Translated by Eggleston, H.G.; Madan, S. Berlin New York: Springer-Verlag. ISBN 3-540-13627-4. OCLC 17499190.
- Bessaga, C.; Pełczyński, A. (1975), Selected Topics in Infinite-Dimensional Topology, Monografie Matematyczne, Warszawa: Panstwowe wyd. naukowe.
- Carothers, Neal L. (2005), A short course on Banach space theory, London Mathematical Society Student Texts, vol. 64, Cambridge: Cambridge University Press, pp. xii+184, ISBN 0-521-84283-2.
- Conway, John (1990). A course in functional analysis. Graduate Texts in Mathematics. Vol. 96 (2nd ed.). New York: Springer-Verlag. ISBN 978-0-387-97245-9. OCLC 21195908.
- Diestel, Joseph (1984), Sequences and series in Banach spaces, Graduate Texts in Mathematics, vol. 92, New York: Springer-Verlag, pp. xii+261, ISBN 0-387-90859-5.
- Dunford, Nelson; Schwartz, Jacob T. with the assistance of W. G. Bade and R. G. Bartle (1958), Linear Operators. I. General Theory, Pure and Applied Mathematics, vol. 7, New York: Interscience Publishers, Inc., MR 0117523
- Edwards, Robert E. (1995). Functional Analysis: Theory and Applications. New York: Dover Publications. ISBN 978-0-486-68143-6. OCLC 30593138.
- Grothendieck, Alexander (1973). Topological Vector Spaces. Translated by Chaljub, Orlando. New York: Gordon and Breach Science Publishers. ISBN 978-0-677-30020-7. OCLC 886098.
- Henderson, David W. (1969). "Infinite-dimensional manifolds are open subsets of Hilbert space". Bull. Amer. Math. Soc. 75 (4): 759–762. doi:10.1090/S0002-9904-1969-12276-7. MR 0247634.
- Khaleelulla, S. M. (1982). Counterexamples in Topological Vector Spaces. Lecture Notes in Mathematics. Vol. 936. Berlin, Heidelberg, New York: Springer-Verlag. ISBN 978-3-540-11565-6. OCLC 8588370.
- Lindenstrauss, Joram; Tzafriri, Lior (1977), Classical Banach Spaces I, Sequence Spaces, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 92, Berlin: Springer-Verlag, ISBN 3-540-08072-4.
- Megginson, Robert E. (1998), An introduction to Banach space theory, Graduate Texts in Mathematics, vol. 183, New York: Springer-Verlag, pp. xx+596, ISBN 0-387-98431-3.
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Riesz, Frederic; Sz.-Nagy, Béla (1990) [1955]. Functional Analysis. Translated by Boron, Leo F. New York: Dover Publications. ISBN 0-486-66289-6. OCLC 21228994.
- Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277.
- Ryan, Raymond A. (2002), Introduction to Tensor Products of Banach Spaces, Springer Monographs in Mathematics, London: Springer-Verlag, pp. xiv+225, ISBN 1-85233-437-1.
- Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
- Swartz, Charles (1992). An introduction to Functional Analysis. New York: M. Dekker. ISBN 978-0-8247-8643-4. OCLC 24909067.
- Trèves, François (2006) [1967]. Topological Vector Spaces, Distributions and Kernels. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-45352-1. OCLC 853623322.
- Wilansky, Albert (2013). Modern Methods in Topological Vector Spaces. Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114.
- Wojtaszczyk, Przemysław (1991), Banach spaces for analysts, Cambridge Studies in Advanced Mathematics, vol. 25, Cambridge: Cambridge University Press, pp. xiv+382, ISBN 0-521-35618-0.


































































































































































































































![{\displaystyle L^{p}([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53d55ccc06ce5cc9ec3bede2be3e7933c206ee3)
![{\displaystyle L^{q}([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a03e8e5b19ee520920c0f1415e1ddb4c59b58d0d)























































![{\displaystyle c_{0},\ell ^{1},L^{1}([0,1]),C([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e865f393700c33f7fed51aa7c595261b480f309c)









































![{\displaystyle L^{p}([0,1]),1\leq p<\infty .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b69acfc70edf4485a1d0bd811608aef03ad523da)

![{\displaystyle C([0,1]).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48046f59cbf686554839918953b0000a1d9ac39b)













![{\displaystyle {\begin{aligned}C(K){\widehat {\otimes }}_{\varepsilon }Y&\simeq C(K,Y),\\L^{1}([0,1]){\widehat {\otimes }}_{\pi }Y&\simeq L^{1}([0,1],Y),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdda0e4532c785e0ccddd2743db91e009ace27bb)

![{\displaystyle L^{1}([0,1],Y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/260abf31df513876af3c866808034d0d771cf448)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

































































































![{\displaystyle \operatorname {BV} ([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f6474e123b8d06d5989e779c17b9084f2ba8314)

![{\displaystyle =V_{f}([a,b])+\lim \nolimits _{x\to a^{+}}f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25115dbc151a6a6ca22cd714e3c0a588ae8c97ab)
![{\displaystyle V_{f}([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a55199983d8408d1891b33b485aa49b3b6cd7fc)
![{\displaystyle \operatorname {NBV} ([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97eacd1b77125924adb034d279f23ccb1aae4cfc)
![{\displaystyle =V_{f}([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3978b950e1c45a40b89de47e166dff3e3f640f90)

![{\displaystyle \operatorname {AC} ([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1215f6bb4f5dcce36b275a1038200a2da63ffc8)
![{\displaystyle \mathbb {F} +L^{\infty }([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef63fd9a8ef0c7df601ba2aa141815ea86073da)
![{\displaystyle W^{1,1}([a,b]).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a982993a7010fe121285b640c096068e79e74874)
![{\displaystyle C^{n}([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e5f2c81e52a668fa74a30946eac00229b1d642f)
![{\displaystyle \operatorname {rca} ([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8788ca02e303b567e9d47a44b0fd48a574ddbfb)
![{\displaystyle =\sum _{i=0}^{n}\sup \nolimits _{x\in [a,b]}\left|f^{(i)}(x)\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cc9f7a9abc638e6fe431d6f36760dbd074b3019)
![{\displaystyle \mathbb {R} ^{n}\oplus C([a,b]),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e48ac47f9406ef46b3c762f19d0d246b54425aa5)

































![{\displaystyle \ \left(C([0,1]),\|\cdot \|_{\infty }\right)\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e82d0b38ba9e9f1c2d851295aab988c53d824749)

![{\displaystyle \ C([0,1])\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd023d5d7505ee1441cff493606c2637a53f6f74)


![{\displaystyle \ \left(L^{1}([0,1]),\|\cdot \|_{1}\right)\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42022aede705a52388aab0e7b1cc2fa79b74d9e3)




![{\displaystyle \left(L^{1}([0,1]),\|\cdot \|_{1}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a6af4e1e53e293d2c3f8ffdf6d0b68c6f576ea0)

































