Langbahn Team – Weltmeisterschaft

Collision cascade

For the scenario of collisions between objects in low earth orbit producing a chain reactions of debris colliding with additional objects producing more debris, see Kessler syndrome.
A classical molecular dynamics computer simulation of a collision cascade in Au induced by a 10 keV Au self-recoil. This is a typical case of a collision cascade in the heat spike regime. Each small sphere illustrates the position of an atom, in a 2-atom-layer-thick cross section of a three-dimensional simulation cell. The colors show (on a logarithmic scale) the kinetic energy of the atoms, with white and red being high kinetic energy from 10 keV downwards, and blue being low.

In condensed-matter physics, a collision cascade (also known as a displacement cascade or a displacement spike) is a set of nearby adjacent energetic (much higher than ordinary thermal energies) collisions of atoms induced by an energetic particle in a solid or liquid.[1][2]

If the maximum atom or ion energies in a collision cascade are higher than the threshold displacement energy of the material (tens of eVs or more), the collisions can permanently displace atoms from their lattice sites and produce defects. The initial energetic atom can be, e.g., an ion from a particle accelerator, an atomic recoil produced by a passing high-energy neutron, electron or photon, or be produced when a radioactive nucleus decays and gives the atom a recoil energy.

The nature of collision cascades can vary strongly depending on the energy and mass of the recoil/incoming ion and density of the material (stopping power).

Linear cascades

Schematic illustration of independent binary collisions between atoms

When the initial recoil/ion mass is low, and the material where the cascade occurs has a low density (i.e. the recoil-material combination has a low stopping power), the collisions between the initial recoil and sample atoms occur rarely, and can be understood well as a sequence of independent binary collisions between atoms. This kind of a cascade can be theoretically well treated using the binary collision approximation (BCA) simulation approach. For instance, H and He ions with energies below 10 keV can be expected to lead to purely linear cascades in all materials.

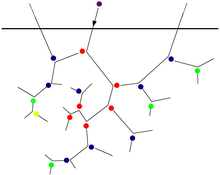
Schematic illustration of a linear collision cascade. The thick line illustrates the position of the surface, and the thinner lines the ballistic movement paths of the atoms from beginning until they stop in the material. The purple circle is the incoming ion. Red, blue, green and yellow circles illustrate primary, secondary, tertiary and quaternary recoils, respectively. In between the ballistic collisions the ions move in a straight path.

The most commonly used BCA code SRIM[3] can be used to simulate linear collision cascades in disordered materials for all ion in all materials up to ion energies of 1 GeV. Note, however, that SRIM does not treat effects such as damage due to electronic energy deposition or damage produced by excited electrons. The nuclear and electronic stopping powers used are averaging fits to experiments, and are thus not perfectly accurate either. The electronic stopping power can be readily included in binary collision approximation[4] or molecular dynamics (MD) simulations. In MD simulations they can be included either as a frictional force [5][6][7][8][9][10][11][12] or in a more advanced manner by also following the heating of the electronic systems and coupling the electronic and atomic degrees of freedom.[13][14][15] However, uncertainties remain on what is the appropriate low-energy limit of electronic stopping power or electron-phonon coupling is.[12][16]

In linear cascades the set of recoils produced in the sample can be described as a sequence of recoil generations depending on how many collision steps have passed since the original collision: primary knock-on atoms (PKA), secondary knock-on atoms (SKA), tertiary knock-on atoms (TKA), etc. Since it is extremely unlikely that all energy would be transferred to a knock-on atom, each generation of recoil atoms has on average less energy than the previous, and eventually the knock-on atom energies go below the threshold displacement energy for damage production, at which point no more damage can be produced.

Heat spikes (thermal spikes)

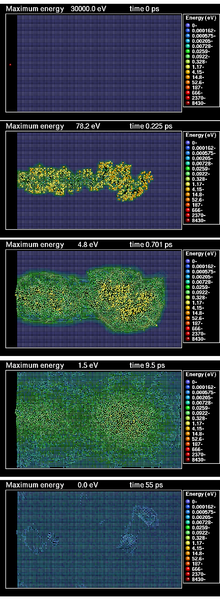
When the ion is heavy and energetic enough, and the material is dense, the collisions between the ions may occur so near to each other that they can not be considered independent of each other. In this case the process becomes a complicated process of many-body interactions between hundreds and tens of thousands of atoms, which can not be treated with the BCA, but can be modelled using molecular dynamics methods.[1][17]

As above, but in the middle the region of collisions has become so dense that multiple collisions occur simultaneously, which is called a heat spike. In this region the ions move in complex paths, and it is not possible to distinguish the numerical order of recoils - hence the atoms are colored with a mixture of red and blue.

Typically, a heat spike is characterized by the formation of a transient underdense region in the center of the cascade, and an overdense region around it.[1][18] After the cascade, the overdense region becomes interstitial defects, and the underdense region typically becomes a region of vacancies.

If the kinetic energy of the atoms in the region of dense collisions is recalculated into temperature (using the basic equation E = 3/2·N·kBT), one finds that the kinetic energy in units of temperature is initially of the order of 10,000 K. Because of this, the region can be considered to be very hot, and is therefore called a heat spike or thermal spike (the two terms are usually considered to be equivalent). The heat spike cools down to the ambient temperature in 1–100 ps, so the "temperature" here does not correspond to thermodynamic equilibrium temperature. However, it has been shown that after about 3 lattice vibrations, the kinetic energy distribution of the atoms in a heat spike has the Maxwell–Boltzmann distribution,[19] making the use of the concept of temperature somewhat justified. Moreover, experiments have shown that a heat spike can induce a phase transition which is known to require a very high temperature,[20] showing that the concept of a (non-equilibrium) temperature is indeed useful in describing collision cascades.

In many cases, the same irradiation condition is a combination of linear cascades and heat spikes. For example, 10 MeV Cu ions bombarding Cu would initially move in the lattice in a linear cascade regime, since the nuclear stopping power is low. But once the Cu ion would slow down enough, the nuclear stopping power would increase and a heat spike would be produced. Moreover, many of the primary and secondary recoils of the incoming ions would likely have energies in the keV range and thus produce a heat spike.

For instance, for copper irradiation of copper, recoil energies of around 5–20 keV are almost guaranteed to produce heat spikes.[21][22] At lower energies, the cascade energy is too low to produce a liquid-like zone. At much higher energies, the Cu ions would most likely lead initially to a linear cascade, but the recoils could lead to heat spikes, as would the initial ion once it has slowed down enough. The concept subcascade breakdown threshold energy signifies the energy above which a recoil in a material is likely to produce several isolated heat spikes rather than a single dense one.

Computer simulation-based animations of collision cascades in the heat spike regime are available on YouTube.[23]

Swift heavy ion thermal spikes

Swift heavy ions, i.e. MeV and GeV heavy ions which produce damage by a very strong electronic stopping, can also be considered to produce thermal spikes[24][25] in the sense that they lead to strong lattice heating and a transient disordered atom zone. However, at least the initial stage of the damage might be better understood in terms of a Coulomb explosion mechanism.[26] Regardless of what the heating mechanism is, it is well established that swift heavy ions in insulators typically produce ion tracks forming long cylindrical damage zones[24][27] of reduced density.[28][29]

Time scale

To understand the nature of collision cascade, it is very important to know the associated time scale. The ballistic phase of the cascade, when the initial ion/recoil and its primary and lower-order recoils have energies well above the threshold displacement energy, typically lasts 0.1–0.5 ps. If a heat spike is formed, it can live for some 1–100 ps until the spike temperature has cooled down essentially to the ambient temperature.[30] The cooling down of the cascade occurs via lattice heat conductivity and by electronic heat conductivity after the hot ionic subsystem has heated up the electronic one via electron–phonon coupling. Unfortunately the rate of electron-phonon coupling from the hot and disordered ionic system is not well known, as it can not be treated equally to the fairly well known process of transfer of heat from hot electrons to an intact crystal structure.[31] Finally, the relaxation phase of the cascade, when the defects formed possibly recombine and migrate, can last from a few ps to infinite times, depending on the material, its defect migration and recombination properties, and the ambient temperature.

Effects

Image sequence of the time development of a collision cascade in the heat spike regime produced by a 30 keV Xe ion impacting on Au under channeling conditions. The image is produced by a classical molecular dynamics simulation of a collision cascade. The image shows a cross section of two atomic layers in the middle of a threedimensional simulation cell. Each sphere illustrates the position of an atom, and the colors show the kinetic energy of each atom as indicated by the scale on the right. At the end, both point defects and dislocation loops remain.

Damage production

Since the kinetic energies in a cascade can be very high, it can drive the material locally far outside thermodynamic equilibrium. Typically this results in defect production. The defects can be, e.g., point defects such as Frenkel pairs, ordered or disordered dislocation loops, stacking faults,[32] or amorphous zones.[33] Prolonged irradiation of many materials can lead to their full amorphization, an effect which occurs regularly during the ion implantation doping of silicon chips.[34]

The defects production can be harmful, such as in nuclear fission and fusion reactors where the neutrons slowly degrade the mechanical properties of the materials, or a useful and desired materials modification effect, e.g., when ions are introduced into semiconductor quantum well structures to speed up the operation of a laser.[35] or to strengthen carbon nanotubes.[36]

A curious feature of collision cascades is that the final amount of damage produced may be much less than the number of atoms initially affected by the heat spikes. Especially in pure metals, the final damage production after the heat spike phase can be orders of magnitude smaller than the number of atoms displaced in the spike.[1] On the other hand, in semiconductors and other covalently bonded materials the damage production is usually similar to the number of displaced atoms.[1][22] Ionic materials can behave like either metals or semiconductors with respect to the fraction of damage recombined.[37]

Other consequences

Collision cascades in the vicinity of a surface often lead to sputtering, both in the linear spike and heat spike regimes.[21] Heat spikes near surfaces also frequently lead to crater formation.[38][39] This cratering is caused by liquid flow of atoms,[40] but if the projectile size above roughly 100,000 atoms, the crater production mechanism switches to the same mechanism as that of macroscopic craters produced by bullets or asteroids.[41]

The fact that many atoms are displaced by a cascade means that ions can be used to deliberately mix materials, even for materials that are normally thermodynamically immiscible. This effect is known as ion beam mixing.[42]

The non-equilibrium nature of irradiation can also be used to drive materials out of thermodynamic equilibrium, and thus form new kinds of alloys.[43]

See also

References

  1. ^ a b c d e R. S. Averback and T. Diaz de la Rubia (1998). "Displacement damage in irradiated metals and semiconductors". In H. Ehrenfest; F. Spaepen (eds.). Solid State Physics. Vol. 51. Academic Press. pp. 281–402.
  2. ^ R. Smith, ed. (1997). Atomic & ion collisions in solids and at surfaces: theory, simulation and applications. Cambridge University Press. ISBN 0-521-44022-X.
  3. ^ SRIM web site
  4. ^ Robinson, M. T. (1974). "Computer Simulation of atomic-displacement cascades in solids in the binary-collision approximation". Phys. Rev. B. 9 (12): 12. Bibcode:1974PhRvB...9.5008R. doi:10.1103/physrevb.9.5008.
  5. ^ Nordlund, K. (1995). "Molecular dynamics simulation of ion ranges in the 1 -- 100 keV energy range". Comput. Mater. Sci. 3 (4): 448. doi:10.1016/0927-0256(94)00085-q.
  6. ^ Beardmore, K. (1998). "An Efficient Molecular Dynamics Scheme for the Calculation of Dopant Profiles due to Ion Implantation". Phys. Rev. E. 57 (6): 7278. arXiv:physics/9901054. Bibcode:1998PhRvE..57.7278B. doi:10.1103/PhysRevE.57.7278. S2CID 13994369.
  7. ^ Caturla, M. (1996). "Ion-beam processing of silicon at keV energies: A molecular-dynamics study". Phys. Rev. B. 54 (23): 16683–16695. Bibcode:1996PhRvB..5416683C. doi:10.1103/PhysRevB.54.16683. PMID 9985796. S2CID 38579564.
  8. ^ Hobler, G. (2001). "On the useful range of application of molecular dynamics simulations in the recoil interaction approximation". Nucl. Instrum. Methods Phys. Res. B. 180 (1–4): 203. Bibcode:2001NIMPB.180..203H. doi:10.1016/s0168-583x(01)00418-9.
  9. ^ Smith, R. (1997). "Molecular Dynamics Simulation of 0.1 -- 2 keV ion bombardment of Ni {100}". Rad. Eff. Def. In Sol. 141 (1–4): 425. doi:10.1080/10420159708211586.
  10. ^ Duvenbeck, A. (2007). "Electron promotion and electronic friction in atomic collision cascades". New J. Phys. 9 (2): 38. Bibcode:2007NJPh....9...38D. doi:10.1088/1367-2630/9/2/038.
  11. ^ Hou, M. (2000). "Deposition of AuN clusters on Au(111) surfaces. I. Atomic-scale modeling". Phys. Rev. B. 62 (4): 2825. Bibcode:2000PhRvB..62.2825H. doi:10.1103/PhysRevB.62.2825. S2CID 123595658.
  12. ^ a b Bjorkas, C. (2009). "Assessment of the relation between ion beam mixing, electron-phonon coupling, and damage production in Fe". Nucl. Instrum. Methods Phys. Res. B. 267 (10): 1830. Bibcode:2009NIMPB.267.1830B. doi:10.1016/j.nimb.2009.03.080.
  13. ^ Pronnecke, S. (1991). "The effect of electronic energy loss on the dynamics of thermal spikes in Cu" (PDF). Journal of Materials Research. 6 (3): 483. Bibcode:1991JMatR...6..483P. doi:10.1557/jmr.1991.0483.
  14. ^ Duffy, D. M. (2007). "Including the effects of electronic stopping and electron-ion interactions in radiation damage simulations". J. Phys.: Condens. Matter. 17 (1): 016207. Bibcode:2007JPCM...19a6207D. doi:10.1088/0953-8984/19/1/016207. S2CID 122777435.
  15. ^ Tamm, A. (2016). "Electron-phonon interaction within classical molecular dynamics". Phys. Rev. B. 94 (1): 024305. Bibcode:2016PhRvB..94a4305L. doi:10.1103/PhysRevB.94.014305.
  16. ^ Sand, A. E. (2014). "Radiation damage production in massive cascades initiated by fusion neutrons in tungsten". J. Nucl. Mater. 455 (1–3): 207. Bibcode:2014JNuM..455..207S. doi:10.1016/j.jnucmat.2014.06.007.
  17. ^ J. Gibson; A. Goland; M. Milgram; G. Vineyard (1960). "Dynamics of Radiation Damage". Physical Review. 120 (4): 1229. Bibcode:1960PhRv..120.1229G. doi:10.1103/PhysRev.120.1229.
  18. ^ F. Seitz; J. S. Koehler (1956). "Displacement of Atoms during Irradiation". In F. Seitz; D. Turnbull (eds.). Solid State Physics. Vol. 2. Academic Press. p. 307.
  19. ^ T. de la Rudia; R. Averback; R. Benedek; W. King (1987). "Role of thermal spikes in energetic displacement cascades". Physical Review Letters. 59 (17): 1930–1933. Bibcode:1987PhRvL..59.1930D. doi:10.1103/PhysRevLett.59.1930. PMID 10035371.
  20. ^ A. Meldrum; S.J. Zinkle; L. A. Boatner; R. C. Ewing (1998). "A transient liquid-like phase in the displacement cascades of zircon, hafnon and thorite" (PDF). Nature. 395 (6697): 56. Bibcode:1998Natur.395...56M. doi:10.1038/25698. hdl:2027.42/62853. S2CID 204996702.
  21. ^ a b R. Aderjan; H. Urbassek (2000). "Molecular-dynamics study of craters formed by energetic Cu cluster impact on Cu". Nuclear Instruments and Methods in Physics Research Section B. 164–165: 697–704. Bibcode:2000NIMPB.164..697A. doi:10.1016/S0168-583X(99)01111-8.
  22. ^ a b K. Nordlund; et al. (1998). "Defect production in collision cascades in elemental semiconductors and fcc metals". Physical Review B. 57 (13): 7556–7570. Bibcode:1998PhRvB..57.7556N. doi:10.1103/PhysRevB.57.7556. S2CID 55789148.
  23. ^ "displacement cascade" Search, YouTube.com
  24. ^ a b A. Meftah; et al. (1994). "Track formation in SiO2 quartz and the thermal-spike mechanism". Physical Review B. 49 (18): 12457–12463. Bibcode:1994PhRvB..4912457M. doi:10.1103/PhysRevB.49.12457. PMID 10010146.
  25. ^ C. Trautmann; S. Klaumünzer; H. Trinkaus (2000). "Effect of Stress on Track Formation in Amorphous Iron Boron Alloy: Ion Tracks as Elastic Inclusions". Physical Review Letters. 85 (17): 3648–51. Bibcode:2000PhRvL..85.3648T. doi:10.1103/PhysRevLett.85.3648. PMID 11030972.
  26. ^ E. Bringa; R. Johnson (2002). "Coulomb Explosion and Thermal Spikes". Physical Review Letters. 88 (16): 165501. arXiv:cond-mat/0103475. Bibcode:2002PhRvL..88p5501B. doi:10.1103/PhysRevLett.88.165501. PMID 11955237. S2CID 11034531.
  27. ^ D. Kanjijal (2001). "Swift heavy ion-induced modification and track formation in materials" (PDF). Current Science. 80: 1560.
  28. ^ P. Kluth; et al. (2008). "Fine Structure in Swift Heavy Ion Tracks in Amorphous SiO2". Physical Review Letters. 101 (17): 175503. Bibcode:2008PhRvL.101q5503K. doi:10.1103/PhysRevLett.101.175503. hdl:10440/862. PMID 18999762.
  29. ^ D. Albrecht; et al. (1985). "Investigation of heavy ion produced defect structures in insulators by small angle scattering". Applied Physics A. 37 (1): 37–46. Bibcode:1985ApPhA..37...37A. doi:10.1007/BF00617867. S2CID 94620228.
  30. ^ A. Struchbery; E. Bezakova (1999). "Thermal-Spike Lifetime from Picosecond-Duration Preequilibrium Effects in Hyperfine Magnetic Fields Following Ion Implantation". Physical Review Letters. 82 (18): 3637. Bibcode:1999PhRvL..82.3637S. doi:10.1103/PhysRevLett.82.3637.
  31. ^ I. Koponen (1993). "Energy transfer between electrons and ions in dense displacement cascades". Physical Review B. 47 (21): 14011–14019. Bibcode:1993PhRvB..4714011K. doi:10.1103/PhysRevB.47.14011. PMID 10005739.
  32. ^ K. Nordlund; F. Gao (1999). "Formation of stacking-fault tetrahedra in collision cascades". Applied Physics Letters. 74 (18): 2720. Bibcode:1999ApPhL..74.2720N. doi:10.1063/1.123948.
  33. ^ M. O. Ruault; J. Chaumont; J. M. Penisson; A. Bourret (1984). "High resolution and in situ investigation of defects in Bi-irradiated Si". Philosophical Magazine A. 50 (5): 667. Bibcode:1984PMagA..50..667R. doi:10.1080/01418618408237526.
  34. ^ E. Chason; et al. (1997). "Ion beams in silicon processing and characterization" (PDF). Journal of Applied Physics. 81 (10): 6513–6561. Bibcode:1997JAP....81.6513C. doi:10.1063/1.365193. Archived from the original (PDF) on 2010-06-23.
  35. ^ V. D. S. Dhaka; et al. (2006). "Ultrafast dynamics of Ni+-irradiated and annealed GaInAs/InP multiple quantum wells". Journal of Physics D. 39 (13): 2659–2663. Bibcode:2006JPhD...39.2659D. doi:10.1088/0022-3727/39/13/004. S2CID 55536038.
  36. ^ A. Kis; et al. (2004). "Reinforcement of single-walled carbon nanotube bundles by intertube bridging". Nature Materials. 3 (3): 153–7. Bibcode:2004NatMa...3..153K. doi:10.1038/nmat1076. PMID 14991016. S2CID 11422662.
  37. ^ K. Trachenko (2004). "Understanding resistance to amorphization by radiation damage". Journal of Physics: Condensed Matter. 16 (49): R1491–R1515. Bibcode:2004JPCM...16R1491T. doi:10.1088/0953-8984/16/49/R03. S2CID 123658664.
  38. ^ R. Webb; D. Harrison (1983). "Computer Simulation of Pit Formation in Metals by Ion Bombardment". Physical Review Letters. 50 (19): 1478. Bibcode:1983PhRvL..50.1478W. doi:10.1103/PhysRevLett.50.1478. hdl:10945/44927. S2CID 120756958.
  39. ^ W. Jäger; K. L. Merkle (1988). "Defect-cluster formation in high-energy-density cascades in gold". Philosophical Magazine A. 57 (3): 479. Bibcode:1988PMagA..57..479J. doi:10.1080/01418618808204681.
  40. ^ M. Ghaly; R. Averback (1994). "Effect of viscous flow on ion damage near solid surfaces". Physical Review Letters. 72 (3): 364–367. Bibcode:1994PhRvL..72..364G. doi:10.1103/PhysRevLett.72.364. PMID 10056412.
  41. ^ J. Samela; K. Nordlund (2008). "Atomistic Simulation of the Transition from Atomistic to Macroscopic Cratering". Physical Review Letters. 101 (2): 027601. Bibcode:2008PhRvL.101b7601S. doi:10.1103/PhysRevLett.101.027601. PMID 18764228. S2CID 15787700.
  42. ^ T. Pugacheva; F. Gjurabekova; S. Khvaliev (1998). "Effects of cascade mixing, sputtering and diffusion by high dose light ion irradiation of boron nitride". Nuclear Instruments and Methods in Physics Research Section B. 141 (1–4): 99–104. Bibcode:1998NIMPB.141...99P. doi:10.1016/S0168-583X(98)00139-6.
  43. ^ Pugacheva, T; Gjurabekova, F; Khvaliev, S (1998). "Effects of cascade mixing, sputtering and diffusion by high dose light ion irradiation of boron nitride". Nuclear Instruments and Methods in Physics Research Section B. 141 (1–4): 99–104. Bibcode:1998NIMPB.141...99P. doi:10.1016/S0168-583X(98)00139-6.
Quelle: http://en.wikipedia.org/wiki/Collision_cascade