Bias in the introduction of variation ("arrival bias") is a theory in the domain of evolutionary biology that asserts biases in the introduction of heritable variation are reflected in the outcome of evolution. It is relevant to topics in molecular evolution, evo-devo, and self-organization.^[1][2] In the context of this theory, "introduction" ("origination") is a technical term for events that shift an allele frequency upward from zero (mutation is the genetic process that converts one allele to another, whereas introduction is the population genetic process that adds to the set of alleles in a population with non-zero frequencies). Formal models demonstrate that when an evolutionary process depends on introduction events, mutational and developmental biases in the generation of variation may influence the course of evolution by a first come, first served effect, so that evolution reflects the arrival of the likelier, not just the survival of the fitter.^{[3][4][5][6][7]} Whereas mutational explanations for evolutionary patterns are typically assumed to imply or require neutral evolution, the theory of arrival biases distinctively predicts the possibility of mutation-biased adaptation. ^[8] Direct evidence for the theory comes from laboratory studies showing that adaptive changes are systematically enriched for mutationally likely types of changes.^{[9][10][11][12]} Retrospective analyses of natural cases of adaptation also provide support for the theory.^[11][13] This theory is notable as an example of contemporary structuralist thinking, contrasting with a classical functionalist view in which the course of evolution is determined by natural selection (see ^[14]).

The theory of biases in the introduction process as a cause of orientation or direction in evolution has been explained as the convergence of two threads.^[15] The first, from theoretical population genetics, is the explicit recognition by theoreticians (toward the end of the 20th century) that a correct treatment of evolutionary dynamics requires a rate-dependent process of introduction (origination) missing from classical treatments of evolution as a process of shifting frequencies of available alleles.^{[16][17][18][19]} This recognition is evident in the emergence of origin-fixation models that depict evolution as a 2-step process of origination and fixation (by drift or selection), with a rate specified by multiplying a rate of introduction (based on the mutation rate) with a probability of fixation (based on the fitness effect). Origin-fixation models ^[19] appeared in the midst of the molecular revolution, a half-century after the origins of theoretical population genetics: they were soon widely applied in neutral models for rates and patterns of molecular evolution; their use in models of molecular adaptation was popularized in the 1990s; by 2014 they were described as a major branch of formal theory.^[19]

The second thread is a long history of attempts to establish the thesis that mutation and development exert a dispositional influence on evolution by presenting options for subsequent functional evaluation, i.e., acting in a manner that is logically prior to selection. Many evolutionary thinkers have proposed some form of this idea. In the early 20th-century, authors such as Eimer or Cope held that development constrains or channels evolution so strongly that the effect of selection is of secondary importance.^[20][21] Early geneticists such as Morgan and Punnett proposed that common parallelisms (e.g., involving melanism or albinism) may reflect mutationally likely changes.^[22] Expanding on Vavilov's (1922) ^[23] exploration of this theme, Spurway (1949) ^[24] wrote that "the mutation spectrum of a group may be more important than many of its morphological or physiological features."

Similar thinking featured in the emergence of evo-devo, e.g., Alberch (1980) suggests that "in evolution, selection may decide the winner of a given game but development non-randomly defines the players" (p. 665)^[25] (see also ^[26]). Thomson (1985), ^[27] reviewing multiple volumes addressing the new developmentalist thinking— a book by Raff and Kaufman (1983) ^[28] and conference volumes edited by Bonner (1982) ^[29]  and Goodwin, et al (1983) ^[30] — wrote that "The whole thrust of the developmentalist approach to evolution is to explore the possibility that asymmetries in the introduction of variation at the focal level of individual phenotypes, arising from the inherent properties of developing systems, constitutes a powerful source of causation in evolutionary change" (p. 222). Likewise, the paleontologists Elisabeth Vrba and Niles Eldredge summarized this new developmentalist thinking by saying that "bias in the introduction of phenotypic variation may be more important to directional phenotypic evolution than sorting by selection." ^[31]

However, the notion of a developmental influence on evolution was rejected by Mayr and others such as Maynard Smith ("If we are to understand evolution, we must remember that it is a process which occurs in populations, not in individuals.") ^[32] and Bruce Wallace ("problems concerned with the orderly development of the individual are unrelated to those of the evolution of organisms through time"), ^[33] as being inconsistent with accepted concepts of causation. This conflict between evo-devo and neo-Darwinism is the focus of a book-length treatment by philosopher Ron Amundson ^[34] (see also Scholl and Pigliucci, 2015 ^[35]). In the theory of evolution as shifting gene frequencies that prevailed at the time, evolutionary causes are "forces" that act as mass pressures (i.e., the aggregate effects of countless individual events) shifting allele frequencies (see Ch. 4 of ^[36]), thus development did not qualify as an evolutionary cause. A widely cited 1985 commentary on "developmental constraints" ^[37] advocated the importance of developmental influences, but did not anchor this claim with a theory of causation, a deficiency noted by critics, e.g., Reeve and Sherman (1993) defended the adaptationist program (against the developmentalists and the famous critique of adaptationism by Gould and Lewontin), arguing that the "developmental constraints" argument simply restates the idea that development shapes variation, without explaining how such preferences prevail against the pressure of selection.^[38] Mayr (1994) ^[39] insisted that developmentalist thinking was "hopelessly mixed up" because development is a proximate cause and not an evolutionary one. In this way, developmentalist thinking was received in the 1980s and 1990s as speculation without a rigorous grounding in causal theories, an attitude that persists (e.g., Lynch, 2007 ^[40]).

In response to these rebukes, developmentalists concluded that population genetics cannot provide a complete account of evolutionary causation: ^[41] instead, a dry statistical account of changes in gene frequencies from population genetics must be supplemented with a wet biological account of changes in developmental-genetic organization (called "lineage explanation" in ^[42]). The beliefs that (1) developmental biology was never integrated into the Modern Synthesis and (2) population genetics must be supplemented with alternative narratives of developmental causation, are now widely repeated in the evo-devo literature and are given explicitly as motivations for reform via an Extended Evolutionary Synthesis. ^[43]

The proposal to recognize the introduction process formally as an evolutionary cause ^[3] provides a different resolution to this conflict. Under this proposal, the key to understanding the structuralist thesis of the developmental biologists was a previously missing population-genetic theory for the consequences of biases in introduction. The authors criticized classical reasoning for framing the efficacy of variational tendencies as a question of evolution by mutation pressure, i.e., the transformation of populations by recurrent mutation. They argued that, if generative biases are important, this cannot be because they out-compete selection as forces under the shifting-gene-frequencies theory, but because they act prior to selection, via introduction. Thus the theory of arrival biases proposes that the generative dispositions of a developmental-genetic system (i.e., its tendencies to respond to genetic perturbation in preferential ways) shape evolution by mediating biases in introduction. The theory, which applies to both mutational and developmental biases, addresses how such preferences can be effective in shaping the course of evolution even while strong selection is at work.

Systematic evidence for predicted effects of introduction biases first began to appear from experimental studies of adaptation in bacteria and viruses. ^{[44] [9]} Since 2017, this support has widened to include systematic quantitative results from laboratory adaptation, and similar but less extensive results from the retrospective analysis of natural adaptations traced to the molecular level (see below). The empirical case that biases in mutation shape adaptation is considered to be established for practical purposes such as evolutionary forecasting (e.g., ^[45]). However, the implications of the theory have not been tested critically in regard to morphological and behavioral traits in animals and plants that are the traditional targets of evolutionary theorizing (see Ch. 9 of ^[15]). Thus, the relevance of the theory to molecular adaptation has been established, but the significance for evo-devo remains unclear. The theory sometimes appears associated with calls for reform from advocates of evo-devo (e.g.,^[46][47]), though it has not yet appeared in textbooks or in broad treatments of challenges in evolutionary biology (e.g.,^[48][49]).

The kind of dual causation proposed by the theory has been explained with the analogy of "Climbing Mount Probable."^[50][2] Imagine a robot on a rugged mountain landscape, climbing by a stochastic 2-step process of proposal and acceptance. In the proposal step, the robot reaches out with its limbs to sample various hand-holds, and in the acceptance step, the robot commits and shifts its position. If the acceptance step is biased to favor higher hand-holds, the climber will ascend. But one also may imagine a bias in the proposal step, e.g., the robot may sample more hand-holds on the left than on the right. Then the dual proposal-acceptance process will show both an upward bias due to a bias in acceptance, and a leftward bias due to a bias in proposal. If the landscape is rugged, the ascent will end on a local peak that (due to the proposal bias) will tend to be to the left of the starting point. On a perfectly smooth landscape, the climber will simply spiral to the left until the single global peak is reached. In either case, the trajectory of the climber is subject to a dual bias. These two biases are not pressures competing to determine an allele frequency: they act at different steps, along non-identical dimensions.

The dual effect predicted by the theory was demonstrated originally with a population-genetic model of a 1-step adaptive walk with 2 options,^[3] i.e., the climber faces two upward choices, one with a higher selection coefficient and the other with a higher mutation rate. A key feature of model is that neither of the alternatives is present in the initial population: they must be introduced. In simulated adaptation under this model, the population frequently reaches fixation for the mutationally favored allele, even though it is not the most fit option. The form of the model is agnostic with respect to whether the biases are mutational or developmental. Subsequent theoretical work (below) has generalized on the theory of one-step walks, and also considered longer-term adaptive walks on complex fitness landscapes. The general implication for parallel evolution is that biases in introduction may contribute strongly to parallelism. The general implication for the directionality and repeatability of adaptive walks is simply that some paths are more evolutionarily favorable due to being mutationally favorable. The general implication for the long-term predictability of outcomes, e.g., particular phenotypes, is that some phenotypes are more findable than others due to mutational effects, and such effects may strongly shape the distribution of evolved phenotypes.

The application of the theory to problems in evo-devo and self-organization relies formally on the concept of a genotype-phenotype (GP) map. The genetic code, for example, is a GP map that induces asymmetries in mutationally accessible phenotypes. Consider evolution from the Met (amino acid) phenotype encoded by the ATG (codon) genotype. A phenotypic shift from Met to Val requires an ATG to GTG mutation; a shift from Met to Leu can occur by 2 different mutations (ATG to CTG or TTG); a shift from Met to Ile can occur by 3 different mutations (to ATT, ATC, or ATA). If each type of genetic mutation has the same rate, i.e., with no mutation bias per se, the GP map induces 3 different rates of introduction of the alternative phenotypes Val, Leu and Ile. Due to this bias in introduction, evolution from Met to Ile is favored, and this is not due to a mutational bias (in the sense of a bias reflecting the mechanisms of mutagenesis), but rather an asymmetric mapping of phenotypes to mutationally accessible genotypes.

As noted above, in the simplest case of the "Climbing Mount Probable" effect, one may consider a climber facing just two fixed choices: up and to the left, or up and to the right. This case is modeled using simulations by,^[3] and is given a more complete treatment by ^[4] In general, the limiting behavior of evolution as the supply of new mutations becomes arbitrarily small, i.e., as , is called "origin-fixation" dynamics .^[19] The origin-fixation approximation for choosing between the left and right options and (respectively) in the Yampolsky-Stoltzfus model is given by the following:

1

where (or ) and (or ) are the mutation rate and selection coefficient for the left (or right) alternative, and assuming that the probability of fixation . In the Yampolsky-Stoltzfus model, this approximation is good for .

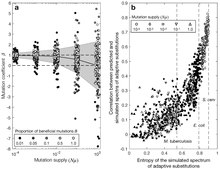
For 1-step walks under origin-fixation conditions, the behavior given by Eqn (1) generalizes from 2 to many alternatives. For instance, Cano, et al. (2022) ^[7] consider a model gene with many different beneficial mutations, and under low mutation supply, the effects of mutation bias are proportional on the spectrum of adaptive changes.

When is not very small, different beneficial alleles may be present simultaneously, competing and slowing down adaptation, an effect known as clonal interference. Clonal interference reduces the effect of mutation bias in models of evolution in finite genetic spaces: alleles favored by mutation still tend to arrive sooner, but before they reach fixation, later-arising alleles that are more beneficial can out-compete them, enhancing the effect of fitness differences. Under the most extreme condition when all possible beneficial alleles are reliably present in a large population, the most fit allele wins deterministically and there is no room for an effect of mutation bias.^[7][51] Stated differently, when all the beneficial alleles are present and selection determines the winner, the chance of success is 1 for the most fit allele, and 0 for all other alleles. Thus, in a gene model with a finite set of beneficial mutations, the influence of mutation bias is expected to be strongest when but to fall off as becomes large.

The influence of mutation under varying degrees of clonal interference can be quantified precisely using the regression method of Cano, et al (2022).^[7] Suppose that the expected number of changes of a given class of mutational changes defined by starting and ending states is directly proportional to the product of (1) the frequency of the starting state and (2) the mutation rate raised to the power of , that is,

beta1

Taking the logarithm of this equation gives

beta2

where is the logarithm of the constant of proportionality. Thus, when is unknown, it may be estimated as the coefficient for the regression of log(counts) on log(expected counts). Simulations of a gene model (figure at right from ^[7]) show a range from under high mutation supply to when the mutation supply is low. While this approach was developed to assess how the mutation spectrum influenced adaptive missense changes (defined by a starting codon and an ending amino acid), the equation reflects a generic framework applicable to any mutationally defined classes of change.

Note that these considerations apply to finite genetic spaces. In an infinite genetic space, clonal interference still slows down the rate of adaptation due to competition, but it does not prevent an effect of mutation bias because there are always mutationally favored alternative alleles among the most-fit class of alleles.^[52][6]

In general, if there is some set of possible steps each with a probability , then the chance of parallelism is given by summing the squares, . It follows from the definition of the variance or the coefficient of variation , that (see Box 2 of ^[52] or Ch. 8 of ^[15])

2

That is, parallelism is increased by anything that decreases the number of choices or increases the heterogeneity in their chances (as measured by or ). This result validates the intuition of Shull ^[53] that "It strains one's faith in the laws of chance to imagine that identical changes should crop out again and again if the possibilities are endless and the probabilities equal" (p. 448). To the extent that heterogeneity in reflects heterogeneity in mutational chances, mutation contributes to parallelism.

In particular, for the case of origin-fixation dynamics, each value of is a product of a mutational origin term and a fixation term, so that heterogeneity in either contributes similarly to the chances of parallelism, and it is possible to partition effects of mutation and selection in accounting for the repeatability of evolution.^[52] Under origin-fixation conditions, and assuming , it follows that ^[54]

3

where and are coefficients of variation for vectors of selection coefficients and mutation rates, respectively. Numeric examples in Box 2 of ^[52] suggest that mutation sometimes contributes more to parallelism than selection, although the authors note that in the denominator above confounds effects of mutation and selection in a hidden way (because, in practice, reflects the set of paths that are sufficiently favored by selection and sufficiently mutationally likely to be observed).

For a systematic view of long-term effects of evolution in discrete genotypic space, consider the 4 perspectives below, focusing on the influence of a mutation spectrum (characteristic for some evolving system) on various ways of defining the chances of evolution (following the treatment by ^[52]):

• A point with access to other nearby points in genotype space. From , there are 0 or more upward steps or paths that differ in mutational favorability (as a function of the mutation spectrum) and fitness benefits. The evolvability-from- is a function of this set of steps. Under simple conditions, each step has a probability and the repeatability of evolution is derived by squaring the values.
• The non-empty set of steps in a path or traverse of increasing fitness, i.e., an adaptive path (one could also consider a neutral path or a path of non-decreasing fitness). Each path has a length and a composition in terms of fitness benefits of steps, and the mutational favorability of steps. The likelihood that evolution follows a given path must depend in some way on these properties, in relation to other possible paths.
• The aggregated set of paths (the "basin of attraction") that lead to a given destination such as a peak or plateau of fitness, or the set of steps into a phenotypic network. Any destination is discoverable via 0 or more upward paths that connect it with lower points. The points in this collection may also have paths to other destinations. For a given destination, the evolvability-to or findability depends on this collection of paths relative to competing paths. Each collection has some total size, i.e., there may be many or few paths leading to a destination.
• A fitness landscape that may include many peaks and paths. Depending on its collection of peaks and paths, a landscape may be more or less navigable, in the sense of having a high chance of finding a peak of high fitness from a randomly chosen starting point. The navigability of a landscape will depend on the mutation spectrum in relation to the composition of paths in the landscape.

Theoretical results relating to each of these perspectives are available. For instance, in a simulation of adaptive walks of protein-coding genes in the context of an abstract NK landscape,^[8] the effect of a GC-AT mutation bias is to alter the protein sequence composition in a manner qualitatively consistent with the analogy of Climbing Mount Probable (above). Each adaptive walk begins with a random sequence and ends on some local peak; the direction of the walk and the final peak depend on the mutation bias.^[8] For instance, adaptive walks under a mutation bias toward GC result in proteins that have more of the amino acids with GC-rich codons (Gly, Ala, Arg, Pro), and likewise, adaptive walks under AT bias result in proteins with more of the amino acids with AT-rich codons (Phe, Tyr, Met, Ile, Asn, Lys). On a rough landscape, the initial effect is similar, but the adaptive walks are shorter.^[8] That is, the mutation bias imposes a preference (on the adaptive walks) for steps, paths, and local peaks that are enriched in outcomes favored by the mutation bias. This illustrates the concept of a directional trend in which the system moves cumulatively in a particular direction along an axis of composition.

The influence of transition-transversion bias has been explored using empirical fitness landscapes for transcription factor binding sites. ^[55] Each landscape is based on generating thousands of different 8-nucleotide fragments and measuring how well they bind to a particular transcription factor. Each peak on each landscape is accessible by some set of paths made of steps that are nucleotide changes, each one being either a transition or a transversion. Among all possible genetic changes, the ratio of transitions to transversions is 1:2. However, the collection of paths leading to a given peak (on a given empirical landscape) has a specific transition-transversion composition that may differ from 1:2. Likewise, any evolving system has a particular transition-transversion bias in mutation. The more closely the mutation bias (of the evolving system) matches the composition bias (of the landscape), the more likely that the evolving system will find the peak.^[55] Thus, for a given evolving system with its characteristic transition-transversion bias, some landscapes are more navigable than others. Navigability is maximized when the mutation bias of the evolving system matches the composition bias of the landscape.^[55]

Finally, rather than organizing genotypes by fitness (in terms of peaks, upward paths, and collections of paths leading to a peak), we can organize genotypes by phenotype using a genotype–phenotype map. A given phenotype identifies a network in genotype-space including all of the genotypes with that phenotype.^[56] An evolving system may diffuse neutrally within the network of genotypes with the same phenotype, but conversions between phenotypes are assumed to be non-neutral. Each phenotypically defined network has a findability that is, as a first approximation, a function of the number of genotypes in the network.^[5][57] For instance, using the canonical genetic code as a genotype-phenotype map, the phenotype Leucine has 6 codons whereas Tryptophan has 1: Leucine is more findable because there are more mutational paths from non-Leucine genotypes. This idea can be applied to the way that RNA folds (considered as phenotypes) map to RNA sequences. For instance, evolutionary simulations show that the RNA folds with more sequences are more findable, and this is due to the way that they are over-sampled by mutation.^[5] A similar point has been made in regard to substructures of regulatory networks ^[58] (see also ^[57]).

The above results apply, as before, to finite spaces. In infinite spaces, the set of remaining beneficial mutations to be explored is infinite and includes an infinite supply of mutationally favored and mutationally disfavored options. Therefore evolution in infinite spaces can continue forever in the mutationally favored direction with no diminution of the mutational effect that applies in the short-term, e.g., one could consider Eqn (1) for such an infinite space. The model of Gomez, et al (2020) ^[6] allows unlimited adaptation via two traits, one with a higher rate of beneficial mutation, and the other with larger selective benefits. In this model, mutation bias continues to be important in long-term evolution even when mutation supply is very high.

The theory of biases in the introduction process as a cause of orientation or direction in evolution may be contrasted with other theories that have been used by evolutionary biologists to reason about the role of variation in evolution:

• Organisms respond adaptively to conditions of life, and these responses are inherited (Lamarckism). This theory is generally considered to lack a mechanistic basis.
• Variation supplies raw material shaped into adaptations by selection (neo-Darwinism). In this theory, "selection is the only direction-giving factor in evolution",^[59] while variation is a material cause— merely a passive source of substance, not a source of form, initiative, or direction (supplied by selection)—, so that the laws of variation "bear no relation" to the structures built by selection.^[60]
• Development imposes prior constraints on form. In this folk theory, "selection may decide the winner of a given game but development non-randomly defines the players." This theory appeared in classic arguments from authors such as Eimer and Cope;^[20] it re-emerged in developmentalist claims of the 1980s.^[25][26]
• Mass conversion by mutation pressure transforms a population. The implications of this mode of causation were worked out mainly by Haldane ^[61] and Kimura,^[62] who found it implausible due to requiring high mutation rates unopposed by selection
• The amount of standing variation enhances or retards selection-driven shifts in quantitative characters. In evolutionary quantitative genetics, the matrix (standing variation) is a source of dimensional but not directional asymmetry, depending on the amount of variation available along any given dimension in trait-space.^[63][64]

Relative to these theories, the theory of arrival biases has distinctive implications, some of which are supported empirically as described below, e.g., the most frequent outcome of an adaptive process such as the emergence of antibiotic resistance is not necessarily the most beneficial, but is often a moderately beneficial outcome favored by a high rate of mutational origin. Likewise, the theory implies that evolution can have directions that are not adaptive, or tendencies that are not optimal, an implication one commentator on Arthur's book^[46] found "disturbing".^[65] This theory is defined, not by any particular problem, taxon, level of organization, or field of study, but by a mechanism defined at the level of population genetics, namely the ability of biases in introduction to impose biases on evolution. Some implications are as follows (see ^[2]).

Effects do not require neutrality or high mutation rates. In contrast to the theory of evolution by mutation pressure explored (and rejected) by Haldane and others, variational dispositions under the theory of arrival biases do not depend on neutral evolution and do not require high mutation rates.^[3]

Graduated biases can have graduated effects. In contrast to what is implied by the language of "constraints" or "limits" employed in historic appeals to internal sources of direction in evolution, the theory of arrival biases is not deterministic and does not require an absolute distinction between possible and impossible forms. Instead, the theory is probabilistic, and graduated biases can have graduated effects.^[3]

Regime-dependency with regard to population genetics. Under the theory, variation biases do not have a guaranteed effect independent of the details of population-genetics. The influence of mutation biases reaches a maximum (proportional influence) under origin-fixation conditions and can disappear almost entirely under high levels of mutation supply.^[7]

Parity in fixation biases and origination biases (under limiting conditions). In classical neo-Darwinian thinking, selection governs and shapes evolution, whereas variation plays a passive role of supplying materials. By contrast, under limiting origin-fixation conditions, the theory of arrival biases establishes a condition of parity such that (for instance) a 2-fold bias in fixation and a 2-fold bias in introduction both have the same 2-fold effect on the chances of evolution.^[19]

Generality with regard to sources of variational bias. In the evolutionary literature, mutation biases, developmental "constraints", and self-organization in the sense of findability are all treated as separate topics. Under the theory of arrival biases, these are all manifestations of the same kind of population-genetic mechanism in which biases in the introduction of variants imposes biases on evolution. Any short-term bias is either a mutational bias in the sense of a difference in rates for two fully specified genotypic conversions, or it can be treated as a scheme of differential phenotypic aggregation over genotypes (see Box 2 of ^[52]).

In addition to these direct implications, some more sophisticated or indirect implications have emerged in the literature.

Non-causal associations induced by mutation and selection. Due to a dual dependence on mutation and selection, the distribution of adaptive changes may show non-causal associations of mutation rates and selection coefficients, somewhat akin to Berkson's paradox, as suggested in Ch. 8 of.^[15] and developed in more detail by Gitschlag, et al (2023).^[66]

Conditions for composition and decomposition of causes. Under limiting origin-fixation conditions, the chances of evolution reflect two factors multiplied together, representing biases in introduction and biases in fixation, as in Eqn (1). Thus, conditions exist under which it is possible to quantify and directly compare the dispositional influences of mutation and selection. This approach has already been used in a few empirical arguments addressed below.^[67][68][50] (Box 2 of ^[52]).

Biased depletion of the spectrum of beneficial mutations. In any case of a system adapting via mutation and selection, there is some set of possible beneficial mutations, characterized by a distribution of selection coefficients and mutation rates. As adaptation occurs in a mutation-biased manner, this spectrum of possible beneficial mutations is depleted in a biased way. The theory for this depletion ^[69] is relevant to experimental work showing that "shifts in mutation spectra enhance access to beneficial mutations".^[70] That is, the experimentally observed favorability of shifts in mutation spectra depends on a pattern of biased depletion of beneficial mutations that is itself a sign of mutation-biased adaptation.

Evidence for the theory has been summarized recently, e.g., Gomez, et al (2020) ^[6] present a table listing 8 different studies providing evidence of effect of mutation bias on adaptation, and Ch. 9 of Mutation, Randomness and Evolution ^[15] is devoted to empirical support for the theory (see also ^[2][52]). Biases in introduction are expected to influence evolution whether neutral or adaptive, but an effect on neutral evolution is not considered intuitively surprising or controversial, and so is not given much attention. Instead, accounts of evidence focus on mutation-biased adaptation, because this highlights how predictions of the theory clash with the classical conception of mutation as a weak pressure easily overcome by selection, per the "opposing pressures" argument of Fisher and Haldane.^[3]

Direct evidence that the spectrum of mutation shapes the spectrum of adaptive changes comes from studies that manipulate the mutation spectrum directly. In one study,^[9] resistance to cefotaxime was evolved repeatedly, using 3 strains of E. coli with different mutation spectra: wild-type, mutH and mutT. The spectrum of resistance mutations among the evolved strains showed the same patterns of spontaneous mutations as the parental strains. Specifically, the transversions favored by mutT (left block of bars) are highly enriched among resistant isolates from mutT parents (blue in the accompanying figure), and likewise, the resistant strains from mutH parents (red) tend to have the nucleotide transition mutations favored by mutH (center block of bars). Thus, changing the mutation spectrum changes the spectrum of adaptive changes in a corresponding manner.

Another study^[12] showed that the AR2 strain of P. fluorescens adapted to the loss of motility overwhelmingly (> 95% of the time) by one specific change, an A289C change in the ntrB gene, while the Pf0-2x strain adapted via diverse changes in several genes. The pattern in AR2 derivatives was traced to a mutational hotspot. Because the hotspot behavior was associated mainly with synonymous differences between the two strains, the experimenters were able to use genetic engineering to remove the hotspot from AR2 and add it to Pf0-2x, without changing the encoded amino acid sequence. This reversed the qualitative pattern of outcomes, so that the modified AR2 (engineered to remove the hotspot) adapted via diverse changes, while the modified Pf0-2x with the engineered hotspot adapted via the A289C change 80% of the time.

A different use of available evidence is to focus on the idea of graduated effects, which distinguishes the theory of arrival biases from the intuitive notion of "constraints" or "limits" on possible forms. In particular, one may set aside the dramatic effects associated with hotspots and mutator alleles, and consider the effects of ordinary quantitative biases in nucleotide mutations. A number of studies have established that modest several-fold biases in mutation can have a several-fold effect on evolution, and some studies indicate a roughly proportional relation between mutation rates and the chances of an adaptive change.^{[11][10][71][72][73]}

For instance, Sackman, et al (2017)^[10] studied parallel evolution in 4 related bacteriophages. In each case, they adapted 20 cultures in parallel, then sequenced a sample of the adapted culture to identify causative mutations. The results showed a strong preference for nucleotide transitions, 29:5 for paths (white vs. black bars in the figure at right) and 74:6 for events. ^[10]

In a study of resistance to Rifampicin in Pseudomonas aeruginosa, MacLean, et al (2010) ^[74] measured selection coefficients and frequency of evolution for 35 resistance mutations in the rpoB (RNA polymerase) gene, and reported mutation rates for 11 of these. The mutation rates vary over a 30-fold range. The frequency with which a resistant variant appears in the set of 284 replicate cultures correlates strongly and roughly linearly with the mutation rate (figure at right). This is not explained by a correlation between selection coefficients and mutation rates, which are not correlated (see Ch. 9 of ^[15]).

As explained above, the influence of the mutation spectrum on the spectrum of adaptive changes can be captured in a single parameter , defined as a coefficient of binomial regression of observed counts on the expected counts from a mutational model.^[7] Based on theoretical considerations, expected values of range from 0 (no influence) to 1 (proportional influence). This method was applied by Cano, et al.^[7] to 3 large data sets of adaptive changes, comparing a model based on independent measures of the mutation spectrum with adaptive changes previously identified in studies of (1) clinical antibiotic resistance of Mycobacterium tuberculosis, (2) laboratory adaptation in E. coli, and (3) laboratory adaptation of the yeast Saccharomyces cerevisiae to environmental stress. In each case, , indicating a roughly proportional influence of mutation bias. The authors report that this is not just due to the influence of transition-transversion bias, because applies both to transition-transversion bias and to the other aspects of the nucleotide mutation spectrum.^[7]

A final use of available evidence is to consider the range of natural conditions under which the theory may be relevant. Whereas laboratory studies can be used to establish causation and assess effect-sizes, they do not provide direct guidance to where the theory applies in nature. As noted in,^[52] most studies of adaptation do not include a genetic analysis that identifies specific mutations, and in the rare cases in which an attempt is made to identify causative mutations, the results typically implicate only very small numbers of changes that are subject to questions of interpretation.^[75] Therefore, the strategy followed in key studies^{[72][11] [13]} has been to focus on trusted cases of adaptation in which the proposed functional effects of putative adaptive mutations have been verified using techniques of genetics.

Payne, et al ^[72] looked for an effect of transition bias among causative mutations for antibiotic resistance in clinically identified strains of Mycobacterium tuberculosis, which exhibits a strong mutation bias toward nucleotide transitions. ^[76] They compared the observed transition-transversion ratio to the 1:2 null expectation under the absence of mutation bias. Using two different curated databases, they found transition:transversion ratios of 1755:1020 and 1771:900, i.e., enrichments 3.4-fold and 3.9-fold over the null, respectively. They also took advantage of the special case of Met-to-Ile replacements, which can take place by 1 transition (ATG to ATA) or 2 different transversions (ATG to ATT or ATC). This 1:2 ratio of possibilities again represents a null expectation for effects independent of mutation bias. In fact, the mutations in resistant isolates have transition-transversion ratios of 88:49 and 96:39 (for the 2 datasets), i.e., 3.6-fold and 4.9-fold above null expectations. This result cannot be due to selection at the amino acid level, because the changes are all Met to Ile. The significance of this result is not that mutation bias only works when the options are selectively indistinguishable: instead, the lesson is that the bias toward nucleotide transitions is roughly 4-fold both for the Met-to-Ile case, and for amino-acid-changing substitutions generally.

A much broader taxonomic scope is implicated in a meta-analysis of published studies of parallel adaptation in nature.^[11] In this study, the authors curated a data set covering 10 published cases of parallel adaptation traced to the molecular level, including well known cases involving spectral tuning, resistance to natural toxins such as cardiac glycosides ^[77] and tetrodotoxin, ^{[78] [79]} foregut fermentation, and so on. The results shown below (table) indicate a transition-transversion ratio of 132:99, a 2.7-fold enrichment relative to the null expectation of 1:2 (the ratio of paths, which is less sensitive to extreme values, is 27:28, a 2-fold enrichment). Thus, this study shows that a bias toward transitions is observed in well known cases of parallel adaptation in diverse taxa, including animals and plants.

Transitions and transversions involved in natural adaptive parallelisms (data from Table 3 of ^[11])

Phenotype	Taxon	Target	Ti counts (paths)	Ti sum	Tv counts (paths)	Tv sum
Insecticide resistance	Insecta	Rdl, Kdr, Ace	2, 2, 5, 2, 3 (5)	14	9, 2, 4 (3)	15
Tetrodotoxin resistance	Vertebrata	Na channels	2, 6, 3 (3)	11	2, 2, 2, 3, 3 (5)	12
Glycoside resistance	Metazoa	𝑁𝑎+/𝐾+-ATPase	4, 4, 2, 2 (4)	12	7, 2, 2, 4 (4)	15
Herbicide resistance	Poaceae	ACCase	5, 2 (2)	7	7, 2, 4, 5 (4)	18
Altitude adaptation	Aves	𝛽-hemoglobin	4, 13 (2)	17	2, 3, 2 (3)	7
Trichromatic vision	Vertebrata	Opsins	2, 5 (2)	7	6, 4, 2 (3)	12
Echolocation	Mammalia	Prestin	2, 2, 2 (3)	6	3, 2 (2)	5
Growth in Ritonavir	HIV1	Protease	25, 7, 9 (3)	41	4 (1)	4
Foregut fermentation	Vertebrata	Ribonucleases	2, 4, 4 (3)	10	NA (0)	0
Benzimidazole resistance	Ascomycota	𝛽-tubulin	7 (1)	7	5, 6 (2)	11
			(28)	132	(27)	99

Finally, Storz, et al.^[13] analyzed changes in hemoglobin affinity associated with altitude adaptation in birds. Specifically, they studied the effect of CpG bias, an enhanced mutation rate at CpG sites due to effects of cytosine methylation on damage and repair, found widely in mammals and birds. ^[80] They assembled a data set consisting of 35 matched pairs of high- and low-altitude bird species. In each case, hemoglobins were evaluated for functional differences resulting in a higher oxygen affinity in the high-altitude species. The changes in affinity plausibly linked to adaptation implicated 10 different paths found a total of 22 different times. Six of the 10 paths involved CpG mutations, whereas only 1 would be expected by chance; and 10 out of 22 events involved CpG mutations, whereas only 2 would be expected by chance (both differences were significant). This enrichment of mutationally-likely genetic changes supports the theory of arrival biases and provides further evidence that predictable effects of mutation bias are important for understanding adaptation in nature.

The theory of arrival bias has been described as a cross-cutting theory ^{[3][1][2][15]} because it proposes a causal grounding (in population genetics) for diverse kinds of pre-existing claims for which a causal grounding is either unknown or mis-specified,

• the developmentalist thesis (above) that evolutionary dispositions may emerge from the way development shapes variation, acting prior to selection (e.g., ^[26])
• a variety of claims in the molecular evolution literature for biased mutational effects (e.g., on codon usage) that are ascribed to unequal or directional "mutation pressure" ^[81] but which are not plausibly explained as evolution by mutation pressure, suggesting instead the need for a theory of mutational biases in introduction;
• the suggestion emerging from the paleobiology debate of the 1980s that, in the hierarchical expansion of evolutionary causation from the population level to multiple levels (i.e., populations, species, higher taxa), speciation is an important source of introduction biases at the level of higher taxa;^[31]
• claims to the effect that evolution tends to find phenotypes over-represented in genotype space, i.e., a "findability" or "arrival of the frequent"^[82] effect that can be recognized both in certain arguments from the molecular evolution literature, e.g., King's (1971) ^[83] explanation for amino acid frequencies, and from the evolutionary self-organization literature, e.g., the arguments of Kauffman^[84]

The context for applying the theory is illustrated in this figure (right). On the left are details of mutation and development that are responsible for tendencies in the generation of variation (varigenesis), i.e., tendencies prior to selection or drift. On the right are observable evolutionary patterns that might possibly be explained by these tendencies. The green arrow is some theory— the theory of arrival biases or some alternative theory— that specifies conditions of a cause-effect relationship linking variational tendencies to evolutionary tendencies. To apply a theory in this context is to generate evolutionary hypotheses or explanations that appeal to the internal details of mutation and development (on the left) to account for evolutionary patterns (on the right) via the conditions of causation specified by the theory. For instance, Darwin's comment that the laws of variation "bear no relation" to the structures built by selection would suggest that there are no conditions under which the internal details on the left account for the patterns on the right. The other theories all suggest that variational tendencies may influence evolution under some conditions. For instance, the theory of mutation pressure applies when mutation rates are high and unopposed by selection, thus it has a limited range of applications. The theory of evolutionary quantitative genetics can be applied very broadly to the evolution of quantitative characters, but the theory (as developed so far) does not suggest that mutation biases will have much impact. ^[85][86][87] By contrast, the theory of arrival bias might apply broadly, and allows for a strong role for variational tendencies in shaping evolutionary tendencies.

Though it seems intuitively obvious today, the theory did not emerge formally until 2001, e.g., as noted above, population geneticists did not propose the theory in the 1980s to answer an evo-devo challenge that literally called for recognizing biases in the introduction of variation. This late emergence has been attributed to a "blind spot" due to multiple factors,^[15] including a tradition of verbal arguments that minimize the role of mutation, a tendency to associate causation with processes that shift frequencies of variants rather than processes that create variants, and a formal argument from population genetics that doesn't extend to evolution from new mutations.

Specifically, when Haldane^[61] and Fisher^[88]  asked if tendencies of mutation could influence evolution, they framed this as a matter of the efficacy of mutation pressure (below), concluding that, because mutation rates are low, mutation is a weak force, only important in the special case of abnormally high mutation rates unopposed by selection. Their conception of evolutionary causation was modeled on selection, which operates by shifting frequencies of available alleles, and so they treated recurrent mutation in the same way. Their conclusion is correct for the case of evolution from standing variation.

More generally, in Modern Synthesis thinking, evolution was assumed to follow from a short-term process of shifting frequencies of available alleles.^[89][90] In this process, mutation is typically unimportant except when the focus is on low-frequency alleles maintained by deleterious mutation pressure (see Population genetics: Mutation), e.g., Edwards (1977) ^[91] addressed theoretical population genetics without considering mutation at all; Lewontin (1974) ^[92] stated that "There is virtually no qualitative or gross quantitative conclusion about the genetic structure of populations in deterministic theory that is sensitive to small values of migration, or any that depends on mutation rates" (p. 267).

The Haldane-Fisher "opposing pressures" argument was used repeatedly by leading thinkers to reject structuralist or internalist thinking (examples in ^[2] or Ch. 6 of ^[15]), e.g., Fisher (1930) stated that “The whole group of theories which ascribe to hypothetical physiological mechanisms, controlling the occurrence of mutations, a power of directing the course of evolution, must be set aside, once the blending theory of inheritance is abandoned." Seventy years later Gould (2002), citing Fisher (1930), wrote that “Since orthogenesis can only operate when mutation pressure becomes high enough to act as an agent of evolutionary change, empirical data on low mutation rates sound the death-knell of internalism.” (p. 510)^[93] 

In this way, arguments from population genetics were used to reject, rather than support, speculative claims about the role of variational tendencies. The flaw in the Haldane-Fisher argument, pointed out in,^[3] is that it treats mutation only as a pressure on frequencies of existing alleles, not as a cause of the origin of new alleles. When alleles relevant to the outcome of evolution are absent initially, biases in introduction can impose strong biases on the outcome. Thus, the late appearance of this theory sheds light on how closely Modern Synthesis thinking was tied to the assumption of standing variation,^[95] and to the forces theory.^[15] These commitments continue to echo in contemporary sources, e.g., in a US white paper endorsed by SSE, SMBE, ASN, ESA and other relevant professional societies, Futuyma, et al (2001) ^[94] state, as fact, that evolution is shifting gene frequencies, identifying the main causes of "evolution" (so defined) as selection and drift (figure).

However, toward the end of the 20th century, theoreticians began to note that long-term dynamics depend on events of mutational introduction not covered in classical theory.^[16][18][17] In the recent literature, the assumption of evolution from standing variation is only rarely made explicit, e.g., ^[96] .^[97] More commonly, evolution from standing variation is presented as an option to be considered together with evolution from new mutations. ^{[98] [19] [99]}

Parallelism and predictability. The application of the theory to parallelism is addressed above. The tendency for particular outcomes to recur in evolution is not merely a function of selection, but also reflects biases in introduction due to differential accessibility by mutation (or, for the case of phenotypes, by mutation and altered development). Recent reviews on prediction ^[52][45] apply the theory to the role of mutation biases in contributing to the repeatability of evolution.

Partitioning causal responsibility for patterns to mutation and selection. In the case of origin-fixation dynamics, evolutionary dispositions can be attributed to a combination of mutation and selection, and it is possible, in principle, to untangle these contributions, as in an analysis of regulatory vs. structural effects in evolution^[67] or patterns of amino acid replacement in protein evolution.^[50]

Evo-devo, GP maps, and findability. The application of the theory of arrival biases to development and phenotypes is mediated by the concept of a genotype-phenotype map. A simple example of a biased induced by a GP map is shown at right. An evolving system diffuses neutrally within the genotypic network for its phenotype, and may occasionally jump to another phenotype. From the starting network of genotypes encoding phenotype P0, there are mutations leading to genotypic networks for P1 and P2. However, the number of mutations leading from the starting network to P2 is 4 times higher illustrating the idea that, for a given developmental-genetic system, some phenotypes are more mutationally accessible. This is not the same thing as a mutation bias per se (an asymmetry caused by the details of mutagenesis), but it can have the same effect in a population-genetic model.^[3] In this case, if all mutations happen at the same rate, the total rate of mutational introduction of P2 is 4 times higher than for P1: this bias can be mapped to the Yampolsky-Stoltzfus model and would have the same implications as a 4-fold mutation bias.

For short-term evolution, what matters is the distribution of immediately mutationally accessible phenotypes. In long-term evolution, however, one may expect two different effects that can be explained by the figure at right, after Fig. 4 of Fontana (2002). ^[56] The networks show the genotypes that map to 3 different phenotypes, P0, P1 and P2. Over time, a system may diffuse neutrally among different genotypes with the same phenotypes. Rarely a jump from one phenotype to another may occur. In the short term, evolution depends only on what is immediately accessible from a given point in genotype space. In the medium-term, evolution depends on the accessibility of alternative phenotype networks, relative to the starting network, e.g., starting with P0, P2 is twice as accessible as P1, even though P1 and P2 have the same number of genotypes. In the long-term, what matters is the total findability of a phenotype from all other phenotypes, which (as a first approximation) is a matter of the number of genotypes (and more precisely is a matter of the total surface area of the network accessible to other high-fitness phenotypes). In this case, P0 is more findable than P1 and P2 because it has twice as many genotypes. The variational bias toward more numerous phenotypes is called "phenotype bias" by Dingle, et al (2022) ^[82] (see also ^[57]).

This effect of findability is the formal basis for empirical and theoretical arguments in studies of the findability of regulatory network motifs^[58] or RNA fold families.^[82] In the figure at right, Dingle, et al. (2022)^[82] present evidence of a striking tendency for the most common RNA folds in nature to match the folds most widely distributed in sequence space.

The theory of arrival biases, proposed in 2001, appears in several subsequent appeals for reform, relative to the neo-Darwinian view of the Modern Synthesis. Per Arthur,^[46] it is part of a developmentalist approach to evolution that emphasizes the internal organizing effects of "developmental reprogramming" on variation. In a different framing per,^[15][2] the efficacy of arrival biases undermines the historic commitment of theoreticians to viewing evolution as a process of shifting gene frequencies in an abundant gene pool, dominated by mass-action forces, and is part of a larger movement (beginning during the molecular revolution) away from the neo-Darwinism of the Modern Synthesis and towards a version of mutationism grounded in population genetics. The theory also has been invoked in the literature of the Extended Evolutionary Synthesis under the heading of Developmental bias.^[47]

The theory of arrival biases focuses on a kind of population-genetic causation linking intrinsic generative biases acting prior to selection with predictable evolutionary tendencies. It is distinct from other ideas that lack the same focus on causation, on intrinsic biases, or on the introduction process.

In classic sources, evolution by "mutation pressure" means the mass transformation of a population by mutational conversion, as in Wilson and Bossert (1971, p. 42^[100][101]). The general assessment of this theory, following Haldane (1932) ^[102]  and Fisher (1930),^[88] is that evolution by mutation pressure is implausible because it requires high mutation rates unopposed by selection. Kimura argued even more pessimistically that transformation by mutation pressure would take so long that it can be ignored for practical purposes.^[62] Nevertheless, later empirical and theoretical work showed that the theory can be valuable in cases such as the loss of a complex trait encoded by many loci, e.g., loss of sporulation in experimental populations of B. subtilis, a case in which the mutation rate for loss of the trait was estimated as an unusually high value, .^[103]

Thus, the theory of mutation pressure and the theory of arrival biases both depict ways for the process of mutation to be an important influence, but they focus on different modes of causation: influencing either the fixation process (mutation pressure) or the introduction process (arrival bias). The effectiveness of mutational tendencies via these two modes is completely different, e.g., only the mutation pressure theory relies on high mutation rates unopposed by selection.

Evolutionary quantitative genetics, the body of theory that focuses on highly polygenic quantitative traits, makes a particular prediction about mutational effects that has some empirical support. In the standard theory for a set of quantitative traits, the standing variation is represented by a matrix of variances and covariances, which depends (in a complex way) on mutational input represented by an matrix. Phenotypic divergence will tend to be aligned (in phenotype space) with the dimension of greatest variation, , and this predicted effect of standing variation has been seen repeatedly.^[104][105]   This effect (explained more fully in Developmental bias) is called adaptation "along genetic lines of least resistance" and could be re-stated (with variation in a positive role) as adaptation along lines of maximal variational fuel. When divergence also aligns with , this suggests that mutational variability shapes divergence, but this circumstantial correlation has other interpretations and is not taken as dispositive evidence.^[106]

The use of mutation bias in the sense of an asymmetric effect on trait means is not part of the standard framework. When mutation bias is included in models of a single quantitative trait under stabilizing selection, the result is a small displacement from the optimal value.^{[87][86] [85]} 

Thus, models in evolutionary quantitative genetics are focusing on a different kind of problem, so that there is no simple translation between (for instance) effects of and effects of biases in introduction.

Evolutionary explanations have often relied on a paradigm of "equilibrium explanation" (ch. 5 of ^[36]) in which outcomes are explained by appeal to what is selectively optimal, without regard to history or details of process (as explained in ^[38] ) However, attention has focused in recent decades on the idea of "contingency", i.e., the idea that the outcome of evolution cannot be explained as the predictable or predefined endpoint of a deterministic process, but takes some path that cannot be predicted easily, or can only be predicted by knowing details of the starting conditions and the subsequent dynamics. "Mutational" contingency refers to cases in which an event of evolution is associated distinctively with a particular mutation, or a mutational hotspot, e.g.,.^[107] in the sense that the evolutionary change would not have happened in the observed manner if the distinctive mutation had not occurred in the manner inferred.

This notion differs from the theory of biases in the introduction process because it is an explanatory concept (rather than a mechanism), applied in idiographic explanations, i.e., explaining one-off events (token events), ^[108] The theory of biases in the introduction process is a theory of general causation: the result of successfully applying the theory is to assign, not a token explanation, but a general explanation like this pattern in which happens more often than is caused by a bias in introduction due to the higher chance of the mutational-developmental conversion .

The concept of "constraint" is fraught. ^[109] Green and Jones (2016)^[110] argue that evolutionary biologists use it as a flexible explanatory concept rather than as a way to refer to a specific causal theory, i.e., a constraint is a factor with some limiting influence that makes it predictive, even if the causal basis of this influence is unclear.

A simple notion of developmental constraint is that some phenotypic forms are not observed, due to being impossible (or at least very difficult) to generate developmentally ^[111] , e.g., centipedes with an even number of leg-bearing segments.^[112] That is, constraint is an explanation for the non-existence of phenotypes based on a variational effect (absence), within a paradigm focused on accounting for patterns of phenotype existence.

Other references to "constraint" imply graduated differences rather than the absolute difference between possible and impossible forms, e.g.,.^[37] Whereas the effectiveness of absolute biases does not require a special causal theory (because a developmentally impossible form is an evolutionarily impossible form), the idea of graduated biases prompts questions of causation, due to the conflict with the classic Haldane-Fisher "opposing pressures" argument, which holds that mere variational tendencies are ineffectual because mutation rates are small. The seminal "developmental constraints" paper by Maynard Smith, et al. (1985) ^[37] noted this issue without providing a solution. Advocates of "constraint" were criticized for failing to provide a mechanism.^[38] This is the issue that Yampolsky and Stoltzfus ^[3] sought to remedy.

Nevertheless, the theory of arrival biases cannot be easily mapped to the concept of "constraint" due to the latter being used widely as a synonym for "factor". In the evo-devo literature, the term "constraint" is increasingly replaced with references to developmental bias. However, the concept of developmental bias is often associated with some idea of facilitated variation or evolvability, whereas the theory of arrival biases is only about the population-genetic consequences of arbitrary biases in the generation of variation.

The theory of arrival biases does not require or imply facilitated variation or directed mutation and is not by itself a theory of the evolution of evolvability. The population-genetic models used to illustrate the theory, and the empirical cases invoked in support of the theory, focus on the effects of different forms of mutation bias, where the bias is always relative to some dimension other than fitness, e.g., transition-transversion bias,^[72] CpG bias,^[13] or the asymmetry of two traits with different mutabilities.^[6] That is, the theory does not assume that biases are beneficial with respect to fitness, and it does not propose that mutation somehow contributes to adaptedness separately from the effect of selection (contra ^[113] ). In fact, many models illustrate the efficacy of arrival biases by focusing on a case where the most mutationally favored outcomes are not the most fit options, as in the original Yampolsky-Stoltzfus model, where one choice has a higher mutation rate but a smaller fitness benefit, and the other has a higher fitness benefit but a smaller mutation rate. The theory assumes neither that mutationally favored outcomes are more fit, nor that they are less fit.

• Developmental bias
• Evolvability
• Extended evolutionary synthesis
• Mutation bias
• Population genetics