Weighted constraint satisfaction problem
In artificial intelligence and operations research, a Weighted Constraint Satisfaction Problem (WCSP), also known as Valued Constraint Satisfaction Problem (VCSP), is a generalization of a constraint satisfaction problem (CSP) where some of the constraints can be violated (according to a violation degree) and in which preferences among solutions can be expressed. This generalization makes it possible to represent more real-world problems, in particular those that are over-constrained (no solution can be found without violating at least one constraint), or those where we want to find a minimal-cost solution (according to a cost function) among multiple possible solutions.
Formal definition
A Weighted Constraint Network (WCN), aka Cost Function Network (CFN), is a triplet where X is a finite set of discrete variables, C is a finite set of soft constraints and is either a natural integer or .
Each soft constraint involves an ordered set S of variables, called its scope, and is defined as a cost function from to where is the set of possible instantiations of S. When an instantiation is given the cost k, i.e., , it is said forbidden. Otherwise it is permitted with the corresponding cost (0 being completely satisfactory).
In WCSP, specific subclass of Valued CSP (VCSP),[1] costs are combined with the specific operator defined as:
- .
The partial inverse of is defined by:
- If , and if , .
Without any loss of generality, the existence of a nullary constraint (a cost) as well as the presence of a unary constraint for every variable x is assumed.
The total cost of a complete instantiation is the bounded sum of the cost of I on for all soft constraint , including the nullary cost and the unary costs for I of the variables in X.
Considering a WCN/CFN, the usual (NP-hard) task of WCSP is to find a complete instantiation with a minimal cost. Other tasks in the related field of graphical model can be defined.[2]
Resolution of binary/ternary WCSPs
Approach with cost transfer operations
Node consistency (NC) and Arc consistency (AC), introduced for the Constraint Satisfaction Problem (CSP), have been studied later in the context of WCSP. Furthermore, several consistencies about the best form of arc consistency have been proposed: Full Directional Arc consistency (FDAC),[3] Existential Directional Arc consistency (EDAC),[4] Virtual Arc consistency (VAC)[5] and Optimal Soft Arc consistency (OSAC).[6]
Algorithms enforcing such properties are based on Equivalence Preserving Transformations (EPTs) that allow safe moves of costs among constraints. Three basic costs transfer operations are:
- Project : cost transfer from constraints to unary constraints
- ProjectUnary : cost transfer from unary constraint to nullary constraint
- Extend : cost transfer from unary constraint to constraint
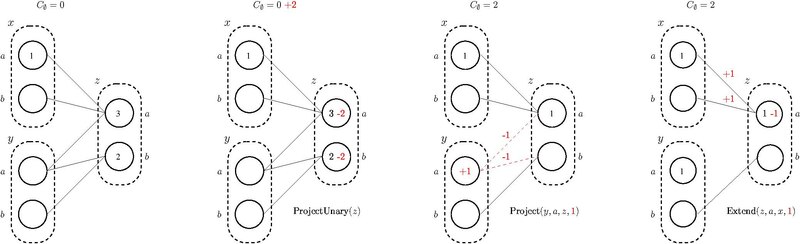
The goal of Equivalence Preserving Transformations is to concentrate costs on the nullary constraint and remove efficiently instantiations and values with a cost, added to , that is greater than or equal to the forbidden cost or the cost of the best solution found so far. A branch-and-bound method is typically used to solve WCSPs, with lower bound and upper bound k.
Approach without cost transfer operations
An alternative to cost transfer algorithms is the algorithm PFC-MRDAC[7] which is a classical branch and bound algorithm that computes lower bound at each node of the search tree, that corresponds to an under-estimation of the cost of any solution that can be obtained from this node. The cost of the best solution found is . When , then the search tree from this node is pruned.
Another more recent approach is based on super-reparametrizations[8] which allows to relax the problem to compute tighter bounds.
Resolution of n-ary WCSPs
Cost transfer algorithms have been shown to be particularly efficient to solve real-world problem when soft constraints are binary or ternary (maximal arity of constraints in the problem is equal to 2 or 3). For soft constraints of large arity, cost transfer becomes a serious issue because the risk of combinatorial explosion has to be controlled.
An algorithm, called GACw-WSTR,[9] has been proposed to enforce a weak version of the property Generalized Arc Consistency (GAC) on soft constraints defined extensionally by listing tuples and their costs. This algorithm combines two techniques, namely, Simple Tabular Reduction (STR)[10] and cost transfer. Values that are no longer consistent with respect to GAC are identified and minimum costs of values are computed. This is particularly useful for efficiently performing projection operations that are required to establish GAC.
Global cost functions with a dedicated semantic (e.g. SoftAllDifferent, SoftAmong) and polytime complexity have been also studied.[11]
Solvers
- https://www.ics.uci.edu/~dechter/software.html
- https://miat.inrae.fr/toulbar2 (based on cost transfer operations)
Benchmarks
Many real-world WCSP benchmarks are available on http://genoweb.toulouse.inra.fr/~degivry/evalgm[12] and https://forgemia.inra.fr/thomas.schiex/cost-function-library (older version at http://costfunction.org/en/benchmark). More MaxCSP benchmarks available on http://www.cril.univ-artois.fr/~lecoutre/#/benchmarks (deprecated site, see also http://xcsp.org/series).
See also
References
- ^ M C. Cooper, S de Givry, and T Schiex. Valued Constraint Satisfaction Problems, pages 185-207. Springer International Publishing, 2020.
- ^ M Cooper, S de Givry, and T Schiex. Graphical models: Queries, complexity, algorithms (tutorial). In 37th International Symposium on Theoretical Aspects of Computer Science (STACS-20), volume 154 of LIPIcs, pages 4:1-4:22, Montpellier, France, 2020.
- ^ M. Cooper. Reduction operations in fuzzy or valued constraint satisfaction. Fuzzy Sets and Systems, 134(3):311–342, 2003.
- ^ S. de Givry, F. Heras, M. Zytnicki, and J. Larrosa. Existential arc consistency: Getting closer to full arc consistency in weighted CSPs. In Proceedings of IJCAI’05, pages 84–89, 2005.
- ^ M. Cooper, S. de Givry, M. Sanchez, T. Schiex, M. Zytnicki. Virtual Arc Consistency for Weighted CSP. In Proceedings of AAAI’08, pages 253-258, 2008.
- ^ M. Cooper, S. de Givry, M. Sanchez, T. Schiex, M. Zytnicki, and T. Werner. Soft arc consistency revisited. Artificial Intelligence, 174(7-8):449–478, 2010.
- ^ E.C. Freuder and R.J. Wallace. Partial constraint satisfaction. Artificial Intelligence, 58(1- 3):21–70, 1992.
- ^ T Dlask, T Werner, and S de Givry. Bounds on weighted CSPs using constraint propagation and super-reparametrizations. In Proc. of CP-21, Montpellier, France, 2021.
- ^ C. Lecoutre, N. Paris, O. Roussel, S. Tabary. Propagating Soft Table Constraints. In Proceedings of CP’12, pages 390-405, 2012.
- ^ C. Lecoutre. STR2: Optimized simple tabular reduction for table constraint. Constraints, 16(4):341–371, 2011.
- ^ D Allouche, C Bessière, P Boizumault, S de Givry, P Gutierrez, J H.M. Lee, KL Leung, S Loudni, JP Métivier, T Schiex, and Y Wu. Tractability-preserving transformations of global cost functions. Artificial Intelligence, 238:166-189, 2016.
- ^ B Hurley, B O'Sullivan, D Allouche, G Katsirelos, T Schiex, M Zytnicki, S de Givry. Multi-Language Evaluation of Exact Solvers in Graphical Model Discrete Optimization. Constraints, 21(3):413-434, 2016.






















