Scalar projection

In mathematics, the scalar projection of a vector $\mathbf {a}$ on (or onto) a vector $\mathbf {b} ,$ also known as the scalar resolute of $\mathbf {a}$ in the direction of $\mathbf {b} ,$ is given by:

s=\left\|\mathbf {a} \right\|\cos \theta =\mathbf {a} \cdot \mathbf {\hat {b}} ,

where the operator $\cdot$ denotes a dot product, ${\hat {\mathbf {b} }}$ is the unit vector in the direction of $\mathbf {b} ,$ $\left\|\mathbf {a} \right\|$ is the length of $\mathbf {a} ,$ and $\theta$ is the angle between $\mathbf {a}$ and $\mathbf {b}$ .^[1]

The term scalar component refers sometimes to scalar projection, as, in Cartesian coordinates, the components of a vector are the scalar projections in the directions of the coordinate axes.

The scalar projection is a scalar, equal to the length of the orthogonal projection of $\mathbf {a}$ on $\mathbf {b}$ , with a negative sign if the projection has an opposite direction with respect to $\mathbf {b}$ .

Multiplying the scalar projection of $\mathbf {a}$ on $\mathbf {b}$ by $\mathbf {\hat {b}}$ converts it into the above-mentioned orthogonal projection, also called vector projection of $\mathbf {a}$ on $\mathbf {b}$ .

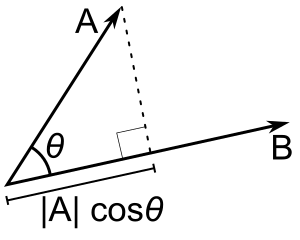
Definition based on angle θ

If the angle $\theta$ between $\mathbf {a}$ and $\mathbf {b}$ is known, the scalar projection of $\mathbf {a}$ on $\mathbf {b}$ can be computed using

s=\left\|\mathbf {a} \right\|\cos \theta .

(

s=\left\|\mathbf {a} _{1}\right\|

in the figure)

The formula above can be inverted to obtain the angle, θ.

Definition in terms of a and b

When $\theta$ is not known, the cosine of $\theta$ can be computed in terms of $\mathbf {a}$ and $\mathbf {b} ,$ by the following property of the dot product $\mathbf {a} \cdot \mathbf {b}$ :

{\frac {\mathbf {a} \cdot \mathbf {b} }{\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|}}=\cos \theta

By this property, the definition of the scalar projection $s$ becomes:

s=\left\|\mathbf {a} _{1}\right\|=\left\|\mathbf {a} \right\|\cos \theta =\left\|\mathbf {a} \right\|{\frac {\mathbf {a} \cdot \mathbf {b} }{\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|}}={\frac {\mathbf {a} \cdot \mathbf {b} }{\left\|\mathbf {b} \right\|}}\,

Properties

The scalar projection has a negative sign if $90^{\circ }<\theta \leq 180^{\circ }$ . It coincides with the length of the corresponding vector projection if the angle is smaller than 90°. More exactly, if the vector projection is denoted $\mathbf {a} _{1}$ and its length $\left\|\mathbf {a} _{1}\right\|$ :