Pentakis icosidodecahedron
Type	Geodesic polyhedron (2,0)
Faces	80 triangles (20 equilateral; 60 isosceles)
Edges	120 (2 types)
Vertices	42 (2 types)
Vertex configuration	(12) 35 (30) 36
Conway notation	k5aD = dcD = uI
Symmetry group	Icosahedral (Ih)
Dual polyhedron	Chamfered dodecahedron
Properties	convex
Net

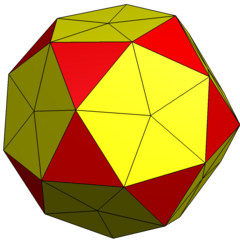
In geometry, the pentakis icosidodecahedron or subdivided icosahedron is a convex polyhedron with 80 triangular faces, 120 edges, and 42 vertices. It is a dual of the truncated rhombic triacontahedron (chamfered dodecahedron).

Its name comes from a topological construction from the icosidodecahedron with the kis operator applied to the pentagonal faces. In this construction, all the vertices are assumed to be the same distance from the center, while in general icosahedral symmetry can be maintained even with the 12 order-5 vertices at a different distance from the center as the other 30.

It can also be topologically constructed from the icosahedron, dividing each triangular face into 4 triangles by adding mid-edge vertices. If this is all that is done, all 80 triangles will be equilateral, but the 4 faces will be coplanar. If the divided edges are lengthened to make the new vertices the same distance from the center as the original vertices, the result is a pentakis icosidodecahedron.

Conway	(u2)I	(k5)aI
Image
Form	2-frequency subdivided icosahedron	Subdivided icosidodecahedron

The pentakis icosidodecahedron is a common geometry for geodesic domes derived from the icosahedron. Buckminster Fuller referred to it as the 2-frequency alternate geodesic subdivision of the icosahedron, because the edges are divided into 2 equal parts and then lengthed slightly to keep the new vertices on a geodesic great circle, creating a polyhedron with two distinct edge lengths and face shapes. An -frequency alternate geodesic subdivision divides each edge into equal parts, and lengthens them as necessary to keep the new vertices on the surface of the same sphere. It produces a polyhedron with triangular faces. The higher the frequency of subdivision, the larger the number of distinct edge lengths and face shapes that will be required, but the more spherical the shape. In the design of geodesic domes, the cost of more roundness is increased complexity.

• 
  Icosidodecahedron
• 
  Pentakis dodecahedron is a slightly smaller Catalan solid which has 60 isosceles triangle faces, 90 edges (2 types), and 32 vertices (2 types).
• 
  Tripentakis icosidodecahedron, the Kleetope of the icosidodecahedron, can be obtained by raising low pyramids on each equilateral triangular face on a pentakis icosidodecahedron. It has 120 isosceles triangle faces (2 types), 180 edges (3 types) and 62 vertices (3 types).
• 
  The nonconvex small icosihemidodecahedron looks like a pentakis icosidodecahedron with inverted pentagonal pyramids meeting at the polyhedron center.

It represents the exterior envelope of a vertex-centered orthogonal projection of the 600-cell, one of six convex regular 4-polytopes, into 3 dimensions.

• Tetrakis cuboctahedron

• George W. Hart, Sculpture based on Propellorized Polyhedra, Proceedings of MOSAIC 2000, Seattle, WA, August, 2000, pp. 61–70 [1]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
  • Chapter 21: Naming the Archimedean and Catalan polyhedra and Tilings (p 284)
• Wenninger, Magnus (1979), Spherical Models, Cambridge University Press, ISBN 978-0-521-29432-4, MR 0552023 Dover 1999 ISBN 978-0-486-40921-4

• VTML polyhedral generator Try "k5aD" (Conway polyhedron notation)