Harmoniskt tal

Inom matematiken är det n:te harmoniska talet summan av reciprokerna av de n första naturliga talen:

H_{n}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}}.

Harmoniska tal är viktiga inom talteori och är nära relaterade till Riemanns zetafunktion och andra speciella funktioner.

Identiteter för harmoniska tal

Direkt av harmoniska talens definition följer differensekvationen

H_{n}=H_{n-1}+{\frac {1}{n}}.

Summan av de n första harmoniska talen ges av

\sum _{k=1}^{n}H_{k}=(n+1)H_{n}-n.

Harmoniska talen är relaterade till Stirlingtalen av andra ordningen enligt formeln

H_{n}={\frac {1}{n!}}\left[{n+1 \atop 2}\right].

Beräkning

En integralrepresentation av Euler är

H_{n}=\int _{0}^{1}{\frac {1-x^{n}}{1-x}}\,dx.

Representationen ovan kan bevisas genom att använda identiteten

{\frac {1-x^{n}}{1-x}}=1+x+\cdots +x^{n-1}.

och integrera termvis.

Genom variabelbytet x = 1−u kan man få ett elegant kombinatoriskt uttryck för H_n :

{\begin{aligned}H_{n}&=\int _{0}^{1}{\frac {1-x^{n}}{1-x}}\,dx\\&=-\int _{1}^{0}{\frac {1-(1-u)^{n}}{u}}\,du\\&=\int _{0}^{1}{\frac {1-(1-u)^{n}}{u}}\,du\\&=\int _{0}^{1}\left[\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}u^{k-1}\right]\,du\\&=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}\int _{0}^{1}u^{k-1}\,du\\&=\sum _{k=1}^{n}(-1)^{k-1}{\frac {1}{k}}{\binom {n}{k}}.\end{aligned}}

Samma representation kan fås genom attanvända den tredje av Retkes identiteter genom att låta $x_{1}=1,\ldots ,x_{n}=n$ och använda $\Pi _{k}(1,\ldots ,n)=(-1)^{n-k}(k-1)!(n-k)!$ :

H_{n}=H_{n,1}=\sum _{k=1}^{n}{\frac {1}{k}}=(-1)^{n-1}n!\sum _{k=1}^{n}{\frac {1}{k^{2}\Pi _{k}(1,\ldots ,n)}}=\sum _{k=1}^{n}(-1)^{k-1}{\frac {1}{k}}{\binom {n}{k}}.

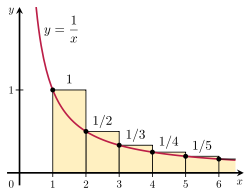
Det nte harmoniska talet växer ungefär lika snabbt som naturliga logaritmen ur n. Orsanken till detta är att

\int _{1}^{n}{1 \over x}\,dx

vars värde är ln(n).

Värdena av följden H_n - ln(n) minskar monotont mot gränsvärdet

\lim _{n\to \infty }\left(H_{n}-\ln n\right)=\gamma ,

där γ ≈ 0.5772156649 är Eulers konstant. Asymptotiska expansionen då n → ∞ är

H_{n}\sim \ln {n}+\gamma +{\frac {1}{2n}}-\sum _{k=1}^{\infty }{\frac {B_{2k}}{2kn^{2k}}}=\ln {n}+\gamma +{\frac {1}{2n}}-{\frac {1}{12n^{2}}}+{\frac {1}{120n^{4}}}-\cdots ,

där $B_{k}$ är Bernoullitalen.

Harmoniska tal som en oändlig serie

Det n-te harmoniska talet kan skrivas som en oändlig serie på följande vis:

{\begin{aligned}1\,+\,{\frac {1}{2}}\,+\,{\frac {1}{3}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{5}}\,+\,\cdots \,+\,{\frac {1}{n}}&=\sum _{r=0}^{n-1}{\frac {1}{n-r}}={\frac {1}{n}}\sum _{r=0}^{n-1}{\frac {n}{n-r}}={\frac {1}{n}}\sum _{r=0}^{n-1}\sum _{m=0}^{\infty }{\frac {r^{m}}{n^{m}}}\\&={\frac {1}{n}}\sum _{r=0}^{n-1}\left(1+\sum _{m=1}^{\infty }{\frac {r^{m}}{n^{m}}}\right)\\&=1+{\frac {1}{n}}\sum _{r=1}^{n-1}\sum _{m=1}^{\infty }{\frac {r^{m}}{n^{m}}}\\&=1+\left(\sum _{m=1}^{\infty }{\frac {1}{n^{m+1}}}\left(\sum _{r=1}^{n-1}r^{m}\right)\right)\\&=1+{\frac {1+2+\cdots +n-1}{n^{2}}}+{\frac {1^{2}+2^{2}+\cdots +(n-1)^{2}}{n^{3}}}+{\frac {1^{3}+2^{3}+\cdots +(n-1)^{3}}{n^{4}}}+\cdots \end{aligned}}

Förekomst

Harmoniska talen förekommer ofta inom talteori och teorin av speciella funktioner såsom i följande formel för digammafunktionen:

\psi (n)=H_{n-1}-\gamma .

Denna relation används ofta som definitionen av harmoniska tal för icke-heltal used n. Harmoniska talen används också ofta till att definiera Eulers konstant γ genom gränsvärdet ovan även om